The Note on Diagonalizable Linear Operators

HUANG Yun-bao

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

The Note on Diagonalizable Linear Operators

HUANG Yun-bao

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

A linear operatorτ∈（）on a finite-dimensional vector spaceis diagonalizable if and only if its minimal polynomial is the product of different linear factors.The paper gives a new proof for the result with elementary symmetric polynomials of its eigenvalues.

vector space；linear operator；diagonalizable operator

Theorem 1 （[1]，Theorem 8.11）A linear operatorτ∈（）on a finite-dimensional vector spaceis diagonalizable if and only if its minimal polynomial mτ（x）is the product of distinct linear factors.

In what follows，we provide a new proof of Theorem 1by making use of elementary symmetric polynomials of the eigenvalues of the operatorτ.

For a positive integern，let i∈｛1，2，…，n｝，k∈｛1，2，…，n－1｝and letσk（i）（x1，x2，…，xn）（or σk（i））denote the kth elementary symmetric polynomial in n－1variables x1，x2，…，xi－1，xi＋1，…，xn，

that is，

From （1）it immediately follows that

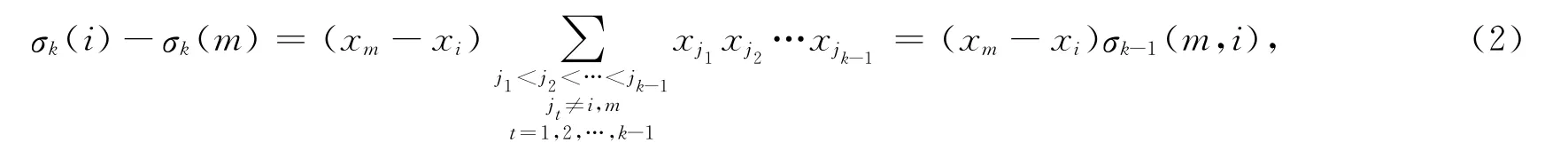
where for m＜i，2≤k，σk－1（m，i）denotes the（k－1）th elementary symmetric polynomial in n－2 variables x1，x2，…，xm－1，xm＋1，…，xi－1，xi＋1，…，xn，andσ0（m，i）＝1.

Now we need to establish the following surprising result on the determinant composed of elementary symmetric polynomials.

Conversely，if mτ（x）is the product of distinct linear factors，then without loss of generality，we assume mτ（x）is of the form （8）.It is sufficient to check（5）holds.

To do so，first，from mτ（τ）＝0it follows that

as a linear combination of the vectorsξ，σ（ξ），…，σk－1（ξ）in order to obtain the following identical relation：

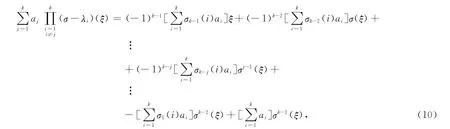
whereσm（i）＝σm（i）（λ1，λ2，…，λk）.

Now we consider the following system of equations in k variables a1，a2，…，ak：

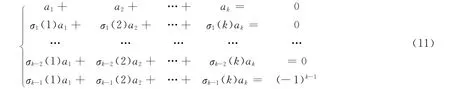
Note that the coefficient determinant of the system of equations（11）is exactly equal toΔ（λ1，λ2，…，λk）.Sinceλ1，λ2，…，λkare different from each other，from Lemma 2we obtainΔ（λ1，λ2，…，λk）≠0.

Thus it follows that the system of equations（11）has a unique solution，which implies there are a1，a2，…，ak∈such that

according to（10）and（9）.Thus（5）holds.

[1]Steven Roman.Advanced linear algebra[M].3th ed，Germany：Springer，2008：196-198.

[2]Zhang Herui，Hao Bingxin.Advanced algebra[M].5th ed，Peking：Advanced Education Press，2007：255-287.

关于可对角化线性算子的一点注记

黄允宝
（杭州师范大学 理学院，浙江 杭州 310036）

域F上有限维向量空间的线性算子τ∈L（）可对角化当且仅当它的极小多项式mτ（x）是F上互异一次因式之积.文章将利用线性算子τ的特征值的初等对称多项式给出此结果的一个新证明.

向量空间；线性变换；可对角化线性变换

O151.2 MSC2010：47A15，47A75Article character：A

1674-232X（2010）05-0321-03

date：2010-06-04

Biography：Huang Yun-bao（1963—），male，born in Yiwu，Zhejiang Province，associate professor，mainly engaged in combinatorics of words.E-mail：huangyunbao＠gmail.com

10.3969／j.issn.1674-232X.2010.05.001