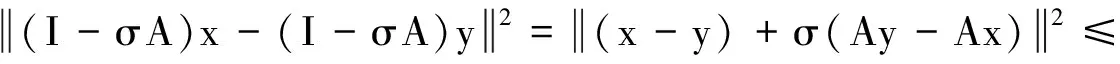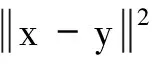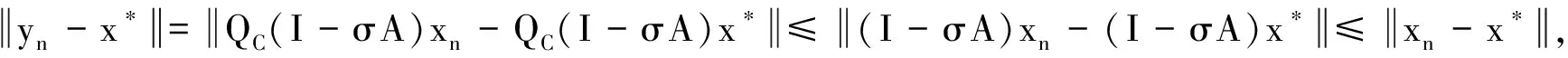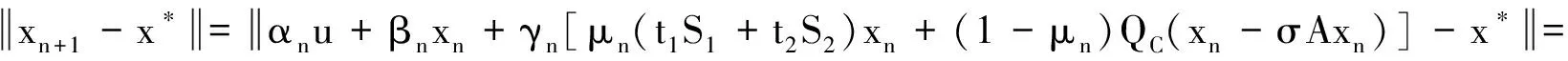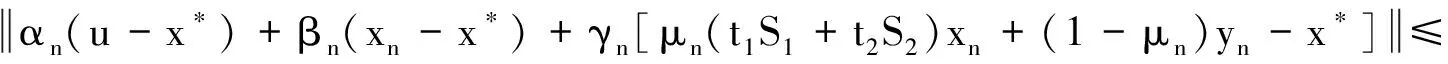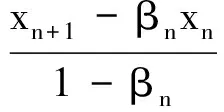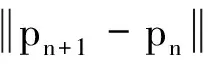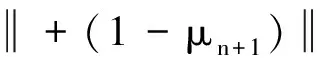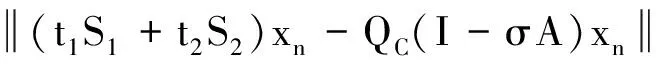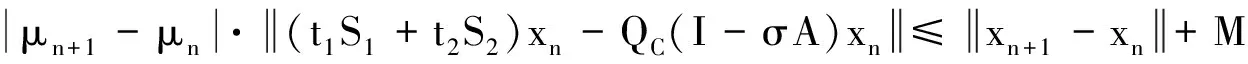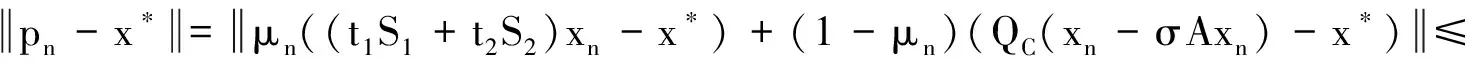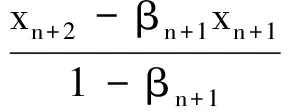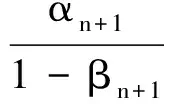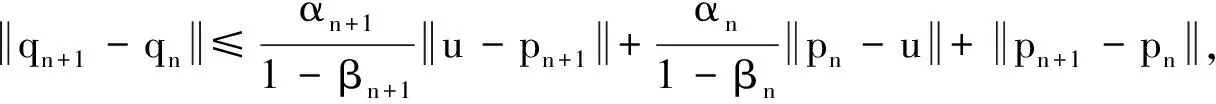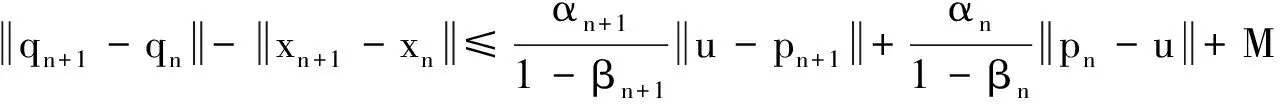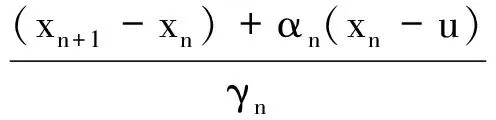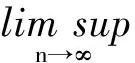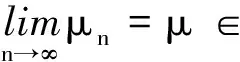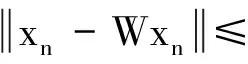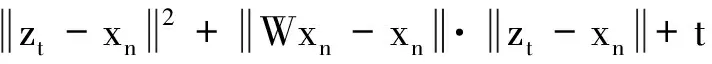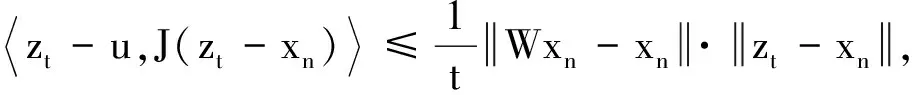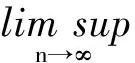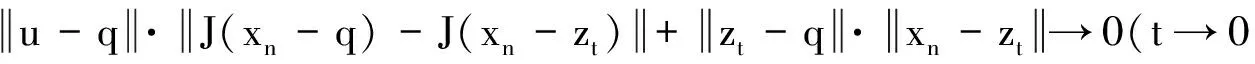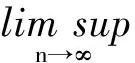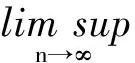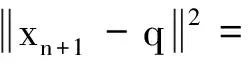关于广义变分不等式的解和严格伪压缩映象不动点的迭代逼近
2010-11-22李付成
李付成,谷 峰
(杭州师范大学 理学院,浙江 杭州 310036)
1 预备知识
在这篇文章中假设E是一个光滑的Banach空间,C是E的一个非空闭凸子集.

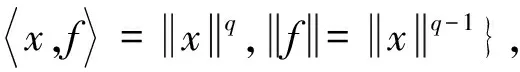
回顾到:
1) 算子A:C→E称为是单调的,如果〈Ax-Ay,J(x-y)〉≥0,∀x,y∈C;
2) 算子A称为是α-强单调的,如果存在一个常数α>0使得
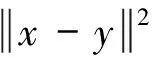
3) 算子A称为是α-拟强单调的,如果存在一个常数α>0使得
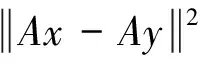
4) 设D⊆C,称Q:C→D是太阳的,如果Q(Qx+t(x-Qx))=Qx,其中Qx+t(x-Qx)∈C,x∈C,t≥0;
5) 映象Q:C→C称作一个保核收缩,如果Q2=Q.如果映象Q:C→C是一个保核收缩,则对所有的z∈R(Q),有Qz=z,其中R(Q)是Q的值域;
6) 子集D⊆C称为是C的一个太阳非扩张收缩核,如果存在一个C到D的一个太阳非扩张保核收缩;
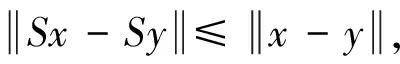
8) 映象S:C→C被称作是λ-严格伪压缩的,如果存在一个常数λ∈(0,1),使得
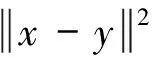
显然,严格伪压缩映象族包含了非扩张映象族作为它的特例.
下面给出一些光滑Banach空间中关于太阳非扩张保核收缩的结果.
命题1[1]设E是光滑Banach空间,C是E的一个非空子集.设Q:E→C是一个保核收缩,并且J是E的正规对偶映象,则下面的条件是等价的.
1)Q是太阳的且非扩张的;
2) 〈x-Qx,J(y-Qx)〉≤0,∀x∈E,y∈C.
命题2[2]设C是一致凸且一致光滑的Banach空间E的一个非空闭凸子集,且T是C到自身的一个非扩张映象,满足F(T)≠∅(F(T)表示映象T的不动点集),则集合F(T)是C的一个太阳非扩张收缩核.
Reich[3]给出,如果E是一致光滑的且D是C到自身的一个非扩张映象的不动点集,则从C到D有一个唯一的太阳非扩张保核收缩,且它能被如下的构造.

最近,Aoyama等[4]考虑了下面的广义变分不等式的问题:
设A:C→E是一个增生算子,找一个点u∈C,使得
〈Au,J(v-u)〉,∀v∈C.
(Ω)
在该文中,用BVI(C,A)来表示变分不等式问题(Ω)的解集.
Aoyama等[4]证明了变分不等式问题(Ω)等价于一个不动点问题.一个元素u∈C是变分不等式(Ω)解的充要条件是u∈C是映象QC(I-λA)的一个不动点,其中I是恒等映象,λ>0是一个常数且QC是E到C的一个太阳非扩张保核收缩.见下面的引理4.
Aoyama等[4]在一致凸且2-一致光滑的巴拿赫空间中得到了一个弱收敛定理如下:
定理AIT设E是一致凸和2-一致光滑的巴拿赫空间,C是E的一个非空闭凸子集.设QC:E→C是一个太阳非扩张保核收缩,α>0,A:C→E是α-一个拟强增生算子,满足S(C,A)≠∅,其中S(C,A)={x*∈C:〈Ax*,J(x-x*)〉≥0,∀x∈C}.如果{λn}和{αn}被给定,使得对于a>0,0 x1=x∈C,xn+1=αnxn+(1-αn)QC(xn-λnAxn),∀n≥1. 该文的目的是,在Banach空间中引进一个更一般的迭代程序,借以寻找两个λ-严格为压缩映象的公共不动点集和一个广义变分不等式解集的公共元素.笔者在一致凸和2-一致光滑Banach空间的框架下,证明了一个强收敛定理,推广和改进了文献[5-9]中的一系列相关结果. 在主要结果中,需要下面的引理. 引理1[10]设{αn}是一个非负实数列,满足αn+1≤(1-γn)αn+δn,其中实数列{γn}⊂(0,1)和{δn}满足下面的条件: 引理3[4]设C是光滑Banach空间E的一个非空闭凸子集,QC是E到C一个太阳非扩张保核收缩,A是C到E的一个增生算子.则对所有的λ>0,有 BVI(C,A)=F(QC(I-λA). 引理4(Bruck[12]) 设C是一个实的严格凸Banach空间E的一个闭凸子集,Si:C→C(i=1,2)是两个非扩张映象,满足F=F(S1)∩F(S2)≠∅.定义Sx=δS1x+(1-δ)S2x,其中δ∈(0,1).则S:C→C是非扩张映象,且F(S)=F≠∅. 引理6[14]设C是一个实2-一致光滑Banach空间E的非空子集,K是最优光滑常数,T:C→C是一个具有常数λ∈(0,1)的严格伪压缩映象.对a∈(0,1),定义Tax=(1-a)x+aTx.则当a∈(0,b)时,Ta是一个非扩张映象且F(Ta)=F(T),其中b=min{1,λ/K2}. 定理1设E是一个一致凸和2-一致光滑的Banach空间,K是最优光滑常数,C是E的一个非空闭凸子集.设QC是E到C的一个太阳非扩张保核收缩,A:C→E是一个α-拟强单调算子.设Ti:C→C是两个具有常数λi∈(0,1)(i=1,2)的严格伪压缩映象.对任意x∈C,定义映象Si:C→C如下:Six=(1-a)x+aTix,其中a∈(0,min{1,λ1/K2,λ2/K2}),F:=F(T1)∩F(T2)∩BVI(C,A)≠∅.假设x1=u∈C,{xn}由下式给出 xn+1=αnu+βnxn+γn[μn(t1S1+t2S2)xn+(1-μn)QC(xn-σAxn)],n≥1, (Δ) 其中σ∈(0,α/K2];{αn},{βn},{γn}和{μn}是(0,1)中的序列.如果序列{αn},{βn},{γn}和{μn}满足以下条件 (iii) 0 则{xn}强收敛到z=QFx,其中QF是C到F的太阳非扩张保核收缩. 证明设x*∈F,则由引理4可知,x*=QC(I-σA)x*.再由引理7可知,S1,S2是两个非扩张映象且Six*=Tix*=x*(i=1,2).下面证明I-σA是非扩张的.由引理2和条件σ∈(0,α/K2],有 这说明I-σA是非扩张的.下面证明{xn}是有界的.事实上,令yn=QC(I-σA)xn,考虑到I-σA是非扩张的,有 (1) 这说明QC(I-σA)也是非扩张的.由yn的定义有 (2) 由Si的非扩张性有 (3) 由(Δ)和(1)有 因此{xn}有界,从而由(1)可知{yn}也都是有界的.令 pn=μn(t1S1+t2S2)xn+(1-μn)QC(xn-σAxn); (4) (5) 对每个n≥1.由(2)和(4),得到 QC(I-σA)xn)+(μn+1-μn)((t1S1+t2S2)xn-QC(I-σA)xn)≤ (6) 由(4)有 xn+1=(1-βn)qn+βnxn,∀n≥1. (7) 由(3)和(4)有 (8) (9) 把(6)代入(9)得 (10) 由(7),得到xn+1-xn=(1-βn)(qn-xn).由(iii)和(10),有 (11) (12) 下面证明 (13) 其中q=QFx.为此,定义映象W:C→C如下: Wx=μ(t1S1+t2S2)x+(1-μ)QC(I-σA)x,∀x∈C, (14) F(W)=F(t1S1+t2S2)∩F(QC(I-σA))= F(S1)∩F(S2)∩BVI(C,A)=F(T1)∩F(T2)∩BVI(C,A)=F, (15) 另外,对任意t∈(0,1),有 (1-t)(〈Wzt-Wxn,J(zt-xn)〉+〈Wxn-xn,J(zt-xn)〉)+ t〈u-zt,J(zt-xn)〉+〈zt-xn,J(zt-xn〉= 由此及(15)得到 (16) 另一方面,有QF(W)u=limt→0zt,F(W)=F.从而则zt→q=QF(W)u(t→0).由于J在E的有界子集上是弱*一致连续的,有 |〈u-q,J(xn-q)〉-〈zt-u,J(zt-xn)〉|≤ |〈u-q,J(xn-q)〉-〈u-q,J(xn-zt)〉|+|〈u-q,J(xn-zt)〉-〈zt-u,J(zt-xn)〉|≤ |〈u-q,J(xn-q)-J(xn-zt)〉|+|〈zt-q,J(xn-zt)〉|≤ 因此,对任意ε>0,存在δ>0,使得对∀t∈(0,δ),有下面的不等式成立 〈u-q,J(xn-q)〉≤〈zt-u,J(zt-xn)〉+ε, 这意味着 由ε的任意性和(16),有lim supn→∞〈u-q,J(xn-q)〉≤0.即 (17) 最后,证明xn→q(n→∞).事实上,因为 αn〈u-q,J(xn+1-q)〉+βn〈xn-q,J(xn+1-q)〉+γn〈pn-q,J(xn+1-q)〉≤ (18) 注1:定理1改进和推广了Cho[6]的相关结果. 易知,在实Hilbert空间中有以下推论成立. 推论1设H是一个实Hilbert空间,C是H的一个非空闭凸子集.设PC是H到C的一个度量投影算子,A:C→H是一个α-拟强单调算子.设T1,T2:C→C是两个非扩张映象.假设F:=F(T1)∩F(T2)∩BVI(C,A)≠∅,x1=u∈C,{xn}由下式给出 xn+1=αnu+βnxn+γn[μn(t1T1+t2T2)xn+(1-μn)PC(xn-σAxn)],n≥1, 其中σ∈(0,2α];{αn},{βn},{γn}和{μn}是(0,1)中的序列.如果序列{αn},{βn},{γn}和{μn}满足以下条件 (iii) 0 (v)t1+t2=1,t1,t2∈(0,1) 则{xn}强收敛到z=PFx,其中PF是C到F的度量投影. [1] Reich S. Asymptotic behavior of contractions in Banach spaces[J]. Math Anal Appl,1973,44(1):57-70. [2] Kitahara S, Takahashi W. Image recovery by convex combinations of sunny nonexpansive retractions[J]. Topol Meth Nonlinear Anal,1993(2):333-342. [3] Reich S. Strong convergence theorems for resolvents of accretive operators in Banach spaces[J]. Math Anal Appl,1980,75:287-292. [4] Aoyama K, Iiduka H, Takahashi W. Weak convergence of an iterative sequence for accretive operators in Banach spaces[J]. Fixed Point Theory Appl,2006(3):13. [5]Cho Y J, Yao Y H, Zhou H Y. Strong convergence of an iterative algorithm for accretive operators in Banach spaces[J]. J Comput Appl Anal,2008,10(1):113-125. [6] Iiduka H, Takahashi W, Toyoda M. Approximation of solutions of variational inequalities formonotone mappings[J]. PanAmer Math J,2004,14:49-61. [7] Iiduka H, Takahashi W. Strong convergence theorems for nonexpansive mappings and inverse-strongly monotone mappings[J]. Nonlinear Anal,2005,61:341-350. [8] Qin Xiaolong, Su Yongfu. Approximation of a zero point of accretive operator in Banach spaces[J]. Math Anal Appl,2007,329(1):415-424. [9] Takahashi W, Toyoda M. Weak convergence theorems for nonexpansive mappings and monotone mappings[J]. Optim Theory Appl,2003,118:417-428. [10] Xu Hongkun. Iterative algorithms for nonlinear operators[J]. London Math Soc,2002,66: 240-256. [11] Xu Hongkun. Inequalities in Banach spaces with applications[J]. Nonlinear Anal TMA,1991,16:1127-1138. [12] Bruck R E. Properties of fixed point sets of nonexpansive mappings in Banach spaces[J]. Tras Amer Math Soc,1973,179:251-262. [13] Suzuki T. Strong convergence of Krasnoselskii and Mann’s type sequences forone-parameter nonexpansive semigroups without Bochne integrals[J]. Math Anal Appl,2005,305:227-239. [14] Zhou H Y. Convergence theorems forλ-strict pseudo-contration in 2-uniformly smooth Banach spaces[J]. Nonlinear Anal,2008,69:3160-3173.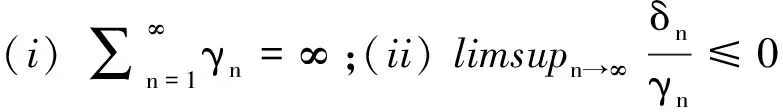
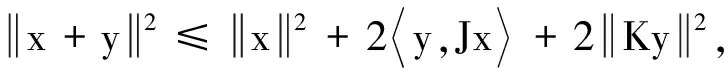
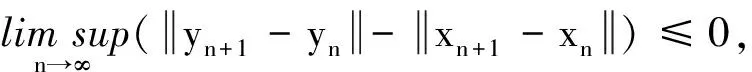
2 主要结果