电场中二维带电谐振子在非对易空间的Wigner函数

车 宇，李 康

(杭州师范大学 理学院,浙江 杭州 310036)

时空坐标非对易的思想由来已久，早在20世纪60多年前就有人提出用时空坐标非对易的概念来解决问题[1-2]．在数学上，有关非对易的讨论很多，但在相当长的一段时间内，非对易几何并未在物理上受到重视．人们在研究物理问题时，时空坐标一般被认为是对易的．近几年来，随着量子霍尔效应以及弦理论的研究，越来越多的非对易背景上的物理学问题得到了人们的广泛关注．对于超弦理论的研究发现，在弦尺度下出现空间的非对易效应[3]．

Wigner函数是著名物理学家Wigner为了对热力学体系做量子修正而引入相空间的一个准概率分布函数[4]．Wigner函数既是量子相空间理论的基础，也是实际应用中最主要的工具之一，尤其是对化学物理问题，它确实具有简单而且物理内涵丰富的特点．而量子谐振子是许多复杂模型的基础，它的Wigner函数积分后能写成简单的表达形式，可用来讨论许多实际问题．这篇文章主要把谐振子模型放在了非对易空间，在有外加电场的情况下，研究二维带电谐振子的Wigner函数．

1 电场中二维带电谐振子的能量本征值和本征函数

先考虑无外加电场的情况下一个质量为μ，频率为ω的二维谐振子，其Hamilton量可表示为[5]

(1)

解其在坐标表象下的Schrödinger方程可得到能量本征值和本征函数，分别为

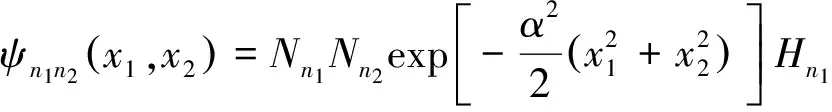
(2)

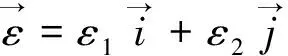
上式中势能项可以写成

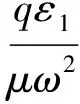
(3)

比较式(1)和式(3)，可知在电场中二维谐振子的能量本征值和本征函数分别为

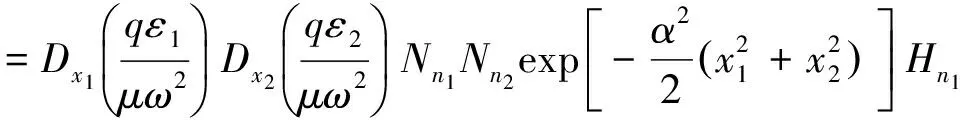
(4)

2 非对易空间中Wigner函数的定义

在非对易空间中Bopp变换[6]满足如下关系：

非对易空间中的薛定谔方程通常又可表示为

H(x,p)*θψnc(x)=Eψnc(x)，

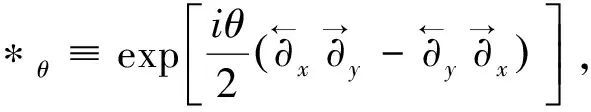
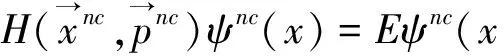
已知在二维对易空间Wigner函数的表达式为

当用Weyl-Moyal乘法(星乘)代替普通乘法时，就得到了在二维非对易空间中Wigner函数的表达式[7]：

(5)

非对易空间中关于Wigner函数的能量本征方程可表示为

(6)

其中

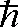
通过Bopp变换，Wigner函数的能量本征方程又可直接写成如下形式：

3 直接积分法求解Wigner函数

首先考虑无外加电场的情况下对易空间中二维谐振子的Wigner函数．为计算方便，将二维非对易空间中Wigner函数的表达式(5)中的星乘表示为如下积分形式[8]：

把二维谐振子的本征函数

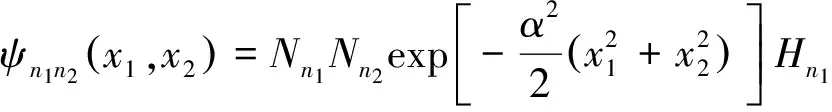
代入二维非对易空间中Wigner函数的表达式中，得到

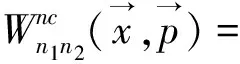
(7)

其中：

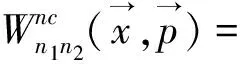
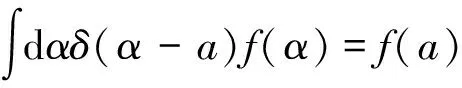
忽略含θ2的高阶小量，则

这就是二维谐振子在非对易空间中用对易空间的坐标和动量表示出来的Wigner函数．

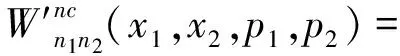
当n1=0,n2=0时，得到基态时的Winger函数：

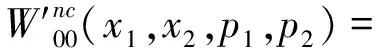
4 解Wigner函数的能量本征方程求Wigner函数

首先考虑无外加电场的情况．在非对易空间中Wigner函数的能量本征方程可以写成

exp(a∂)f(x)=f(x+a)可知

(8)

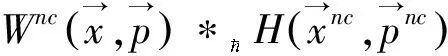
(9)

二维谐振子在非对易空间的Hamiltonian可表示为(令μ=1,ω=1)

将上式分别代入式(8)和(9)得

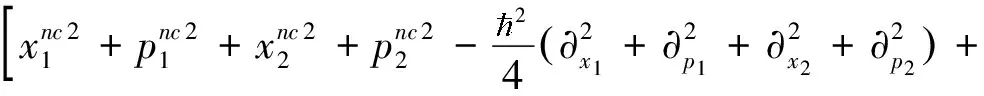
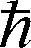
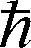
对比以上两式，得到

(10)

引入两个新的变量ξ和η：

则式(10)可写成

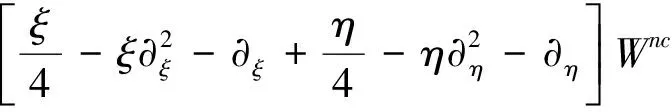
(11)

令Wnc(ξ,η)=Wnc(ξ)Wnc(η)，E=E1+E2由上式可得到

(12)

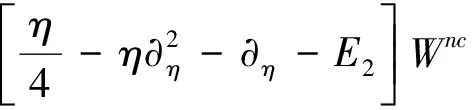
(13)

将Wnc(ξ)定义如下：

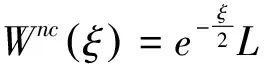
则由式(12)可推导出函数L(ξ)满足的方程为

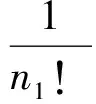
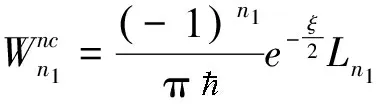
将变量ξ和η代入上式，得到非对易空间中二维谐振子的Wigner函数为

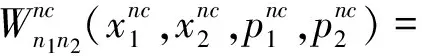
通过Bopp变换，并忽略含θ2的高阶小量，最后得到用对易空间中坐标和动量表示出非对易空间的二维谐振子的Wigner函数为

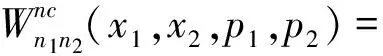
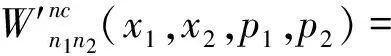
当n1=0,n2=0时，得到基态时的Winger函数

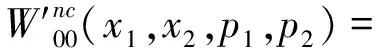
5 结 论

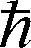
[1] Snyder H S. Quantized space time[J]. Phys Rev,1947,71:38.

[2] Snyder H S. The electromagnetic field in quantized space-time[J]. Phys Rev,1947,72:68.

[3] Seiberg N, Witten E. String theory and non-commutative geometry[J/OL]. High Energy Physics-Therom(1999-11-03)[2010-01-12].http://arxiv.org/abs/hep-th/9908142

[4] Wigner E. On the quantum correction for thermodynamic equilibrium[J]. Phys Rev,1932,40:749-759.

[5] 车宇，李康.非对易相空间下电场中二维带电谐振子的Wigner函数[J].杭州师范大学学报:自然科学版,2010,9(1):43-47.

[6] Chaichian M, Sheikh-Jabbari M M, Tureanu A. Hydrogen atom spectrum and the lamb shift in noncommutative QED[J]. Phys Rev Lett,2001，86(13)：2716-2719.

[7] Wang Jianhua, Li Kang, Dulat Sayipiamal. Wigner functions for harmonic oscillator in non-commutative phase space[J/OL]. High Energy Physics-Therom(2009-08-12)[2010-01-12].http://arxiv.org/abs/hep-th/0908.1703

[8] Wang Jianhua, Li Kang, Dulat Sayipiamal,etal. Wigner functions for Klein-Gordon oscillators in non-commutative space[J/OL]. High Energy Physics-Therom(2009-08-12)[2010-01-12].http://arxiv.org/abs/hep-th/0908.1703