基于VAR方法的我国股市风险管理实证研究

尹 念

(1.湘潭大学商学院,湖南湘潭 411105;

2.湖南财政经济学院,湖南长沙 410205)

基于VAR方法的我国股市风险管理实证研究

尹 念1,2

(1.湘潭大学商学院,湖南湘潭 411105;

2.湖南财政经济学院,湖南长沙 410205)

基于我国风险管理的实际情况,介绍了风险价值(VAR)、GARCH模型及在其框架下计算波动率和估计分布临界值的过程和步骤,在此基础上,使用 GARCH模型拟合沪深 300综指收益率序列的波动率,并用以预测日 VAR,估计结果显示我国股市的日 VAR值仍相对较高,与发达国家金融市场的发展水平仍然有很大差距,监管部门应该具备风险管理意识,提高风险管理能力,更好地防范市场风险。

风险价值;VAR;GARCH模型

伴随着我国金融机构自身业务的不断发展和创新,我国金融市场正逐步走向成熟。根据中金所2010年 3月 26日发布的《关于沪深 300股指期货合约上市交易有关事项的通知》,正式公布沪深 300股指期货合约自 2010年 4月 16日起上市交易。在中金所发布的此项通知中,沪深 300股指期货首批上市合约分别为 2010年 5月、6月、9月和 12月合约,挂盘基准价将由中金所在上市前一个工作日公布。股指期货的正式推出为我国对冲市场风险,实行套期保值提供了一个良好的途径,进一步完善了我国的金融体系。但是,我们必须清醒的认识到期货合约的风险远比原生股票市场大,因此,在不断深化金融创新的同时,我们应将国际上成功的风险管理技术有选择地应用于中国的证券市场,以增强证券市场的抗风险能力,从而推动衍生工具市场的进一步发展和完善。以VAR方法为代表的风险管理技术在西方发达国家广泛应用于各大银行及金融机构中,收到了良好的效果。笔者在对VAR方法进行简要介绍的基础上,通过核密度方法对正态分布假定的修正和引入 GARCH模型估计波动性的基础上计算我国沪深 300综指的风险值,估计结果显示这一修正方法比一般的德尔塔——正态方法更为精确。

一、使用 GARCH模型计算我国股票综合指数

1、VAR概述

随着金融自由化和金融创新的不断深化,金融机构所承担的风险越来越难以衡量,风险管理者需要一种既便于掌握和理解,又能准确反映金融机构所承担的特定风险的技术方法。VAR(Value at Risk)方法正是在此背景下产生的,并且与压力测试、情景分析和返回检验等一系列方法共同组成了风险管理的 VAR体系。[1]目前,VAR方法被广泛应用于各大国际金融机构的市场风险和信用风险管理领域,国际清算银行也已经允许各国银行使用以VAR风险框架为基础的内部模型来计算针对市场风险和信用风险的资本充足率。

根据菲利浦 ·乔瑞《VAR风险价值──金融风险管理新标准》一书中的描述,VAR的直观定义是指:在一定的置信水平下和一定的目标期间内,预期的最大损失。更严格的说,VAR描述了在一定的目标期间内收益和损失的预期分布的分位数。[1]通常情况下,要建立VAR模型必须首先确定 4个要素:一是确定持有期限,持有期限是衡量收益波动性和关联性的时间单位,也是取得观察数据的频率,如所观察数据是日收益率、周收益率或者月收益率等。二是确定观察期。观察期是对给定持有期限收益波动性和关联性考察的整体时间长度,是整个数据选取的时间范围,如在未来 6个月或者 1年的观察期内考察回报率的波动性。三是选择置信水平。置信水平过低,会导致损失超过VAR值的极端事件发生概率过高,使得VAR值失去意义;置信水平过高,则会导致超过VAR值的极端事件发生概率降低,由于统计样本中反映极端事件的数据很少,VAR值估计的准确性也会下降。四是确定概率密度函数。该函数是资产组合在既定持有期限内回报率的概率分布。理论上,如果能够得到投资组合中所有金融工具的收益分布以及整个组合的收益分布,那么 VAR值就可以很容易地计算出来。

对于一般分布计算 VAR,我们假定W0为初始投资额,R为投资收益率,那么在投资期末目标投资组合的价值为W=W0(1+R)。若收益率 R的均值为μ,波动率(方差)为σ,那么该投资组合的VAR可以简单的表述为 VAR=αW0σ。根据笔者的理解,VAR的计算一方面依赖于对分布的精确估计以得到分位值α,这需要针对收益序列分布的尖峰厚尾效应及左偏效应做出很好的归纳;另外一方面就涉及估计波动性参数σ,由于σ在很多情况下多变的特征,因此,使用 GARCH模型估计波动性就是一个很好的方法。

2、GARCH模型

使用 GARCH模型拟合波动率的估计效果是比较好的,能对序列的波动聚集效应、厚尾效应及时变方差效应很好地拟合波动行为。[3]这样,我们就可以应用 GARCH模型估算时变条件方差,即上文所提及的σ2t,用它开方即可得到σt,其计算如下:

这样,再由 VAR的计算表达式 VAR=αW0σ0,我们就可以计算得到VARt估计值。

3、运用 GARCH模型计算VAR的具体计算过程与步骤

第一步,根据所选定的置信水平运用核密度法估计α。

第三步,计算我国沪深 300综合指数日收益率的市场风险 VARt值。

二、GARCH模型的实证分析

1、数据来源

我们选用 2005年 4月 8日到 2010年 3月 26日沪深 300综合指数共 1208个交易日的日收盘价数据①进行分析,据此计算每一交易日的收益率序列,得到收益率的时间序列数据记作 rt。这里我们将收盘价转化为收益率序列,用收益率序列的方差或标准差来衡量其综合指数 VAR。假设深沪 300综合指数第 t个交易日的收益率为 rt,其近似计算公式为:

其中,pt为第 t个交易日的收盘价; pt-1为第 t-1个交易日的收盘价。

2、收益率序列的性质及其检验

第一,收益率序列及其波动率序列

首先,我们比较一下上证与深证综合指数收益率序列及其波动率序列的基本情况,具体见图 1。

图1 沪深 300综合指数收益率及波动率图

由图1我们可以有一个直观的认识,沪深 300综合指数的波动率序列有明显的聚类效应。从中可以看出综指在 2006年至 2007年间的波动率相当大。因此,根据图 1我们可以认为,应用 GARCH模型进行拟合数据是比较合理的。

第二,收益率序列的平稳性和正态性检验

由于我们假定计算收益率序列的VAR是基于其数据服从正态分布假定的前提下,即假设,简单收益率 {rt|t=1,…,T}是独立的,且都服从一个固定均值和方差的正态分布。这个假设使得资产收益率的统计性质变得可以处理,但是这一正态假定在实际运算中却可能存在问题,这就又回到了我们之前讨论的收益率序列经验上存在厚尾和左偏效应的问题上,由于篇幅有限,笔者只计算两序列的正态性检验统计量及其偏度和峰度值,进一步的分析修正留待今后去完成。我们对沪深 300综合指数收益率数据的分布进行正态检验,具体数据见下表 1。

表1 沪深 300综合指数收益率数据的正态性检验统计量表

从上表 1我们可以看出,序列的检验统计量 P值均很小(小于 0.05),故我们认为序列均不服从正态性假定。在以上检验的基础上,我们可以认为在正态假定下计算VAR会存在很大的偏差,故我们使用核密度法估计序列 0.05显著性水平下的临界值,计算得到的沪深 300综合指数的百分之五的临界值为 -4.127763。

第三,收益率序列的平稳性检验

使用ADF检验方法检验两序列的平稳性,两点检验规则是:第一将滞后期选为 3,第二将显著性水平选在 5%;在此基础上对上证与深证综合指数1208天的收益率数据进行时间序列的单位根检验,由于D.G.P未知,我们首先是对含有漂移项、确定性趋势项的完备模型设定形式进行检验,由检验结果得知,确定性时间趋势项的 t值不显著,对去除了确定性时间趋势项后的序列进行 ADF检验,检验结果如下,沪深 300综合指数收益率的 ADF统计量值为 -15.5358,其 P值为 0.01,结果在 5%显著性水平下拒绝原假设,因此,我们认为沪深 300综合指数收益率的时间序列数据是平稳的。

第四,收益率序列的自相关和偏自相关检验

在以上检验的基础上,我们又做了沪深 300综合指数收益率自相关与偏自相关函数,以及沪深300综合指数收益率自相关函数,具体结果见图 2和图 3。

图2 沪深 300综合指数收益率自相关与偏自相关函数图

图3 沪深 300综合指数平方收益率自相关函数

由以上两个图我们可以发现沪深 300综合指数的偏自相关函数均存在多阶滞后,且阶数均较大,这样可能用一个MA模型拟合其均值方程会较好。此外,由上证和深证综合指数平方收益率自相关函数我们可以发现,两序列存在较明显的序列不独立,据此判断可能存在 GARCH效应。

第五,GARCH模型的估计

由上可知沪深 300综合指数收益率时间序列是平稳的,且具有聚集效应和时变方差效应,同时由于两个时间序列均不服从正态分布,我们又根据核密度法估计出了他们的参数临界值,所以,在此基础上我们使用 GARCH模型对沪深300综合指数收益率的波动率进行建模,试图拟合其时变波动率用以估算序列的VAR值。

我们借助软件对这 1208个交易日收盘价的收益率进行拟合,由该序列的相关图和偏自相关图我们先对模型拟合 MA(1)-GARCH(1,1)模型,结果显示沪深 300综指的模型拟合不显著,因此,修改去掉MA模型,使用 GARCH(1,1)模型在此进行回归,回归结果较为显著,具体回归结果见表2。

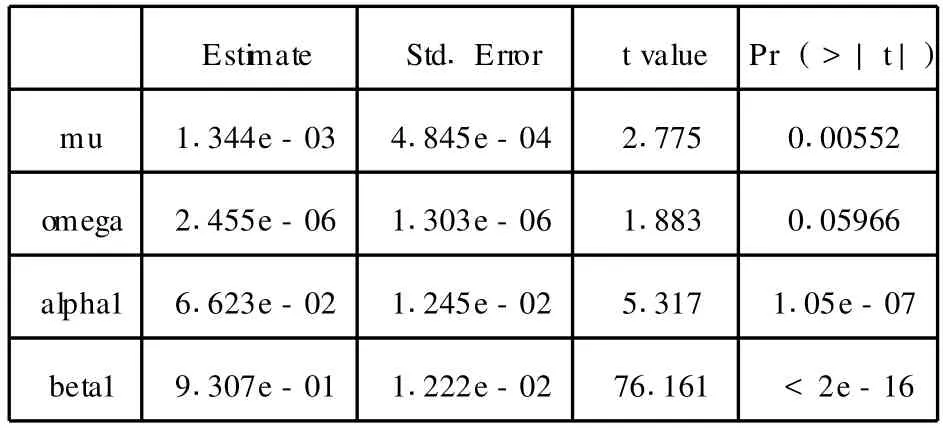
表2 沪深 300综指拟合数据表

第六,使用估计的 GARCH模型对收益率序列波动率进行预测

我们使用上文所估计的波动率模型对沪深 300综指的波动率进行预测,这里假定初始资产为 1元,则我们可以计算得到 2010年 3月 29日(27、28日停盘)的一日VAR值。例如,3月 29日沪深 300综指的波动率(标准差)预测值为 0.01288641,则沪深 300综指的一日 VAR预测值为 -4.127763,其乘以 0.01288641,为 0.053192元。

另外,我们可以发现使用核密度法估计的分布临界值远大于正态分布的临界值,分位数大概在 4左右,但正态分布的 95%置信水平的分位数为1.64,远小于核密度估计的分位数值(VAR值为0.0252573元),故我们可以认为使用一般的德尔塔——正态方法在很大程度上会低估市场风险的 VAR值,故使用以上修正方法更为合理。

三、结语

笔者尝试使用 GARCH模型拟合沪深300综指收益率序列的波动率,并用以预测日 VAR,估计结果显示我国股市的日VAR值仍相对较高,也就是说我国的股市风险相对西方发达国家来说较大。[4]虽然近些年来,随着我国金融体制改革的不断深入,我国金融市场得到了迅猛发展,并引起了全世界的广泛关注,但是我们应该清醒地认识到,整个金融市场体制和机制的转换将是一个长期的过程,我国与发达国家金融市场的发展水平仍然有很大差距,因此,监管部门更应该具备风险管理意识,提高风险管理能力,更好地防范市场风险。

【注 释】

①数据来自 CS MAR数据库。可从 www.grarsc.com中股票市场系列中的 CS MAR中国股票市场交易数据库下载。

[1]菲利浦·乔瑞 .VAR风险价值——金融风险管理新标准[M].上海:立信出版社,2000.67-69.

[2]Ruey S.Tsay.金融时间序列分析 [M].北京:机械工业出版社,2005.24-27.

[3]Campbell,Lo,Mackinlay.,The Econometrics of FinancialMarkets[M].Princeton University Press,1997.109-112.

[4]李基梅,刘青青 .VAR-GARCH模型在我国股指期货风险管理中的应用 [J].山东理工大学学报(自然科学版),2008,(7):12-15.

The Positive Research on Stock Risks Management in Ch ina Based on VARMethod

YIN Nian1,2
(1.Business College Xiangtan University,X iangtan Hunan 411105;2.Hunan University of Finance and Econom ics,Changsha Hunan 410205)

Based on the current situation of risk management in China,this article introducesVAR and GARCH model and how to use them to calculate fluctuation rate and estimate distributing critical value.By using GARCH model,it predicates the fluctuation rate of the Hushen 300 index yield rate sequence andVAR per day.For there are still great disparity between China and developed countries,we should increase risk management ability to prevent further problems.

value of risk;VAR;GARCH Model

F830.91

A

1009-4148(2010)05-0063-04

2010-09-15

尹 念(1982- ),女,湖南益阳人,湘潭大学商学院硕士研究生,湖南财政经济学院会计师

(编辑:芝山;校对:朱恒)