帆板驱动时的卫星姿态前馈补偿控制

2010-12-11斯祝华刘一武

空间控制技术与应用 2010年6期

关键词：帆板姿态控制姿态

斯祝华，刘一武

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190)

帆板驱动时的卫星姿态前馈补偿控制

斯祝华1,2，刘一武1,2

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190)

研究帆板驱动影响下的卫星姿态控制问题.帆板驱动时存在转速波动，从而影响卫星姿态.在已有帆板驱动模型的基础上，分析帆板转速特性，通过对帆板转速的离线拟合和在线估计，结合卫星姿态动力学模型，设计了卫星姿态的一般前馈补偿和自适应前馈补偿控制器.数学仿真结果表明，两种前馈补偿控制均能有效克服由帆板驱动不平稳而造成的对星体干扰，实现卫星姿态高精度控制.

帆板驱动; 姿态控制; 前馈补偿

卫星在轨运行期间，太阳电池帆板要相对星体转动以跟踪太阳，从而获取更多能量.由于步进电机定位精度高，无累积误差，加上电机可开环控制，驱动线路简单，因而在太阳帆板驱动装置(SADA，solar array drive assembly)中得到广泛应用.但电机模型复杂，动态响应差，加上电机自身谐波力矩和机构摩擦力矩的影响，通常帆板转动时存在转速波动，直接影响卫星姿态[1].

目前有关SADA驱动机理及其对星体姿态影响的研究较少.卫星姿态控制器设计没有考虑由其引起的扰动，或者是采用鲁棒控制方法[2]，而没有从模型角度研究二者关系.SADA研制机构更多的专注于设计驱动性能更好的帆板驱动机构[3-4].SADA驱动同星上运动部件(如扫描镜、天线等)运动具有相似性，对于带可动部件的卫星，仅利用反馈的卫星姿态控制系统不能及时克服扰动干扰，一般采用补偿控制技术，即将可动部件产生的干扰提供给卫星姿态控制系统，通过对卫星平台的控制减小干扰影响.文献[5]针对带扫描相机的预警卫星，提出一种前馈—反馈复合控制方法.在反馈控制的基础上，利用角动量定理，估计出相机扫描运动产生的角动量扰动，以此作为前馈补偿控制器的输入.文献[6]针对带运动天线的卫星提出了一种自适应控制方法，根据卫星姿态信号对天线未知参数在线估计，以实时修正前馈补偿模型.文献[7]针对平台和附件同时机动时的复合控制技术做了初步探索.文献[8]针对一类复杂卫星，设计了基于自适应模糊逻辑和干扰补偿的控制器.

前馈补偿控制精度很大程度上取决于补偿模型的准确度.在文献[9]中，作者提出了一种较为全面系统的SADA驱动模型，并用试验测试验证了所建模型的合理性和准确性.本文在该SADA驱动模型的基础上分析了帆板转速特性，并基于帆板转速离线拟合和在线估计，设计了卫星姿态的一般前馈补偿和自适应前馈补偿控制.数学仿真结果表明，本文提出的前馈补偿能有效克服因帆板驱动不平稳而造成的对星体扰动，实现卫星姿态高精度控制.

1 系统模型

1.1卫星运动学与动力学模型

图1所示为本文所要研究的卫星构型，它由中心刚体和单翼太阳帆板组成，帆板绕其自身转轴旋转以对日定向.obxbybzb为卫星本体坐标系，osxsyszs为帆板坐标系.初始时刻，卫星本体系与帆板系方位一致，姿态参考系为卫星轨道坐标系.

图1 中心刚体带单翼太阳帆板卫星构型

采用欧拉角描述卫星姿态.定义卫星滚动角φ、俯仰角θ和偏航角ψ，记Θ=[φθψ]T为卫星姿态，在小角度近似前提下，卫星姿态运动学方程为

式中：δ=[-ω0ψ-ω0ω0φ]T，ω0为轨道角速度.

带帆板驱动的卫星动力学方程组如下：

1.2帆板驱动模型

以直接驱动型SADA为研究对象，它由两相混合式步进电机以双四拍方式带动帆板转动，电机采用正余弦细分电流驱动.SADA驱动方程[9]如下：

(5)

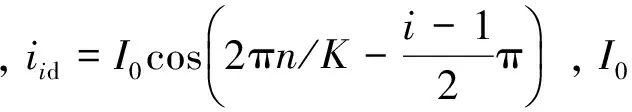
2 控制器设计

对式(2)描述的卫星而言，随着帆板转角变化，卫星转动惯量阵、耦合系数阵也随之变化，这给控制器设计带来不便.工程上常用冻结参数法，即将帆板转角固定在某一定值，模型转为定常系统，然后针对定常系统设计控制器.经典PID控制律原理简单，易于实现，参数调节灵活，因此在实际工程中得到广泛应用.PID反馈控制器参数[11]可按下式近似选取：

式中：BW为控制系统带宽；KP、KI、KD为3×3对角阵，分别为PID控制器的比例、积分和微分增益；I0为3×3对角阵，其对角元素值对应帆板转角为45°时的整星三轴转动惯量值.

考虑到帆板驱动带来的影响，下面设计一种带前馈补偿的卫星姿态稳定控制器，

式中：Tbc、Tfc分别为反馈控制量和前馈补偿量，前馈控制量Tfc用于补偿帆板驱动带来的扰动.

结合式(1)、(2)，若前馈补偿量

则卫星姿态可克服帆板驱动带来的干扰.由于帆板转角、卫星姿态角、角速度可测，因此若能知道帆板实时转速，则式(14)可以求解.下面设计基于帆板转速模型的两种前馈补偿方法.

2.1一般前馈补偿

当系统为开环时，通过求解式(2)，得

(15)

通常帆板驱动力矩主要由步进电机产生，步进电机驱动控制带宽相比姿态控制要大得多，从而帆板转角、转速动态响应相比卫星姿态要快得多，因此，在设计卫星姿态控制器时，可认为帆板转角实际响应与指令响应相同.

根据上述两点，可以将帆板驱动系统看作独立系统，通过帆板驱动模型来单独研究帆板转速波动特性.

对某一固定的细分驱动方案，帆板转速波动主要受粘性摩擦系数和电机四次齿槽力矩影响[9]，因而可通过对这两个参数的选取来拟合帆板转速的波动，从而帆板转速可以显式表示.

对某一指令转速，从文献[9]的数学仿真和试验测试结果看，帆板正转时，帆板转速为半正弦特性曲线.帆板转速可采用如下表达式拟合：

(16)

式中：ωmax、ωmin分别为转速最大、最小波动幅值；T为转速波动周期；t0为电机克服摩擦力矩而导致的相角偏差；t为自帆板驱动开始起经历的时间，可由电机驱动脉冲计数器等效折算;mod(t,T)为取模运算，结果为t/T的余数.

由式(16)可得

(17)

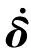
2.2自适应前馈补偿

显然2.1节前馈补偿要求帆板驱动模型有一定的准确性，而且还需要帆板驱动的实测数据，另外，采用式(16)拟合帆板转速必然引起拟合误差，因此，2.1节所述前馈补偿只是一种近似补偿.

粘性摩擦系数主要影响帆板驱动初期的转速波动，谐波力矩影响转速的谐波频率成分和波动幅值，当采用文献[9]中提出的谐波电流补偿时，帆板转速只含有电机步进的基频分量，于是可认为电机经电流补偿后，帆板转速只含有基频分量，这样帆板转速可用正弦函数表示

(18)

式中：c0为已知的平均转速；c1与c2一起描述了转速波动的幅值和相位，为未知参数.显然，转速采用这种描述是不够严谨的，为此提出一种自适应方法，以减少由此转速模型拟合造成的误差.该方法基于角动量守恒定理，研究模型采用角动量形式描述

式中H0为初始角动量.

结合式(18)，得

(20)

式中：M0(α)=JsD；M1(α)=JsDsin(4Zrα)；M2(α)=JsDcos(4Zrα).

对系统(20)设计如下自适应控制律：

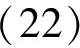
将式(22)代入式(20)，得

(23)

因此，当参数估计很准时，由帆板驱动引起的角动量可相互抵消.

定理1.系统(20)在式(21)和式(22)中描述的自适应补偿控制器的作用下，且满足条件

时，系统为渐近稳定的，即当t→∞时，有Θ→0.

证明.预选Lyapunov函数

对上式关于时间求导，得

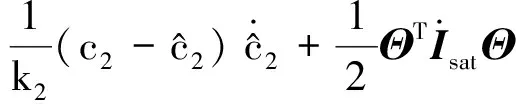
联立式(21)～(23)，有

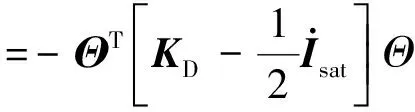
由于帆板转速较小，因此容易根据条件(24)选择参数.

3 仿真算例

为验证上述补偿控制效果，下面比较仿真了无前馈补偿PD控制、一般力矩前馈补偿控制和自适应前馈补偿控制3种控制器的作用效果.仿真对象为中低轨道带单翼帆板驱动的卫星，轨道角速度(帆板指令转速)为0.06(°)/s.

卫星模型参数如下：

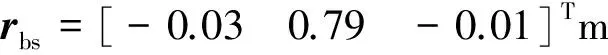
SADA驱动模型参数见表1.

取系统带宽0.04rad/s，阻尼系数0.707，自适应参数估计增益k1=k2=0.5.卫星姿态角、姿态角速度、帆板转角和转速初始值均为0.

表1 SADA驱动模型参数

以0.06(°)/s转速为例，将SADA驱动独立出来，对上述帆板驱动进行仿真，通过仿真结果，得到如下帆板转速拟合表达式：

(28)

仿真表明，帆板驱动对卫星俯仰轴姿态影响较大.图2和图3分别为在PD控制、一般前馈补偿控制和自适应前馈补偿控制作用下的卫星俯仰轴姿态角和姿态角速度变化曲线.表2汇总了3种控制方法的控制精度.从表2可以看出，经前馈补偿后，卫星星体姿态角和角速度都能提高一个数量级，前馈补偿控制精度主要取决于前馈补偿模型的精确性，一般前馈补偿采用的是对帆板转速离线拟合，具有针对性，自适应前馈补偿是在线辨识帆板转速，具有一般性.

图4为帆板实际转速、离线拟合转速与在线估计转速.从中可以看出，帆板转速含有0.2Hz频率成分，即电机5s步进1个步距角0.3°，符合中低轨道帆板平均转速0.06(°)/s的要求.但受电机步进工作方式影响，帆板转速有明显的波动，转速保持在0.051～0.073(°)/s范围内，由于要克服机构摩擦力矩作用，帆板转动初期较大，进入稳态后，波动幅值受谐波力矩影响.另外，可以看出两种方法都具有一定精度的逼近拟合帆板转速，从而确保了补偿模型的准确性.

图2 3种控制器作用下的卫星俯仰角

图3 3种控制器作用下的卫星俯仰角速度

表2 3种控制器控制性能比较

4 结论

本文针对帆板驱动影响下的卫星姿态控制问题，从卫星动力学模型和帆板驱动模型出发，设计了两种卫星姿态前馈补偿控制器.在已有SADA驱动模型基础上分析帆板转速特性，通过对帆板转速的离线拟合和在线估计，设计了卫星姿态的一般前馈补偿和自适应前馈补偿控制.数学仿真结果表明，通过前馈补偿可以有效克服因帆板驱动不平稳而造成的对星体扰动，实现卫星姿态高精度控制.

[1] 高星, 王友平. 太阳电池阵驱动机构的通用化、系列化和组合化设计[J]. 空间科学学报, 2002, 22(增2): 55-68

[2] 李英堂, 费从宇. 帆板转动时卫星姿态的非线性控制[J]. 宇航学报, 2001, 22(1): 31-36

[3] Patrick S, Christine E. High performance stepper motor for space mechanisms[R]. NASA N95-27271, 1995

[4] Rajagopal K R, Singh B, Singh B，et al. An improved high resolution hybrid stepper motor for solar array drive of Indian remote sensing satellite[J]. IEEE Trans. on Industry Applications, 1997, 33(4): 906-913

[5] 魏世隆, 曹喜滨, 张世杰. 具有运动部件的预警卫星姿态前馈复合控制[J]. 航天控制, 2004, 22(3): 45-49

[6] Yamada K，Yoshikawa S. Adaptive attitude control for an artificial satellite with mobile bodies[J]. Journal of Guidance, Control and Dynamics, 1996, 19(4): 948-953

[7] 苟兴宇, 陈义庆, 李铁寿，等. 平台与附件同时机动及其复合控制初探[J]. 空间控制技术与应用, 2009, 35(5): 1-5

[8] 王佐伟, 刘一武. 基于自适应模糊逻辑和干扰补偿的航天器姿态控制[C]. 第25届中国控制会议, 哈尔滨, 2006

[9] 斯祝华, 刘一武, 黎康. 太阳帆板驱动装置建模及其驱动控制研究[J]. 空间控制技术与应用, 2010, 36(2): 13-19

[10] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998

[11] Markley F L, Bauer F H，Femiano M D. Attitude control system conceptual design for geostationary operational environmental satellite spacecraft series[J]. Journal of Guidance, Control and Dynamics, 1995, 18(2): 247-255

[12] Slotine J J E，Li W P. Applied nonlinear control[M]. New Jersy: Prentice Hall, 1991

AttitudeFeed-ForwardControlforaSatellitewithaRotatingSolarArray

SI Zhuhua1,2，LIU Yiwu1,2

(1.BeijingInstituteofControlEngineering,Beijing100190,China; 2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190,China)

The attitude control of a satellite under the influences induced by solar array driving is studied in this paper. There exists a fluctuation of driving speed of solar array, so the attitude is affected due to the coupling function. Based on the model of solar array driving issued before, the driving speed of solar array is analyzed. Then through offline fit and online estimation, combining with the attitude dynamics model, an attitude control with normal or adaptive feed-forward compensation is designed. Simulation results demonstrate that this two feed-forward controllers can overcome the disturbance caused by the rough driving of solar array and, as a result, the high accuracy attitude control can be achieved.

solar array driving; attitude control; feed-forward compensation