线值方阵的变换方法及最小圈值的估算
2010-12-07黄文旭
黄文旭
(海南师范大学 数学与统计学院,海南 海口 571158)
线值方阵的变换方法及最小圈值的估算
黄文旭
(海南师范大学 数学与统计学院,海南 海口 571158)
主要讨论有向图的线值方阵的变换方法及最小圈值的估算问题,得到了线值方阵可作等差变换、换法变换、倍法变换的方法以及这些变换方法的性质,线值方阵的最小圈值的估算定理.
线值方阵;变换;最小圈值
货郎问题(Travelling Salesman Problem)又称推销商问题,是组合优化论中的一个著名问题[1-4],与图论中的哈密尔顿圈(Hamiltonian cycle)的问题相关[5].线值方阵的引进主要是针对这一问题而提出的[6-8].本文主要讨论一般有向图的线值方阵的若干变换方法以及最小圈值的估算问题,目的在于为线值方阵的最小圈值及最短圈元素的计算提供新的途径.
1 基本概念
1.1 图的概念
概念1所谓一个有向图(简称图)G=G(V,X)是由有n个点的非空集合V=V(G)和预先给定的V中不同点的m个有序对构成的集合X组成;称V为图G的点集,每个P∈V称为图G的点;称X为图G的线集,X中的每一个有序对(Pi,Pj)称为图G的一条有向线,也称由点Pi到点Pj的线;记为PiPj,并称点Pi为起点,点Pj为终点(本文所论的图没有以同一点为起点与终点的线)[7].
概念 2设 G=G(V,X)为有向图,P1,P2,…,Pk是V中的k个互异点.如果线集C={P1P2,P2P3,…,Pk-1Pk}⊆X则称C为图G中由点P1到点Pk的一条开路,记为C:P1P2P3…Pk-1Pk,且称点Pi为 C的起点,点Pk为C的终点;如果线集C={P1P2,P2P3,…,Pk-1Pk,PkP1}⊆X则称C为图G的一条闭路,记为C:P1P2P3…Pk-1PkP1;开路与闭路统称为路.当{P1,P2,P3,…,Pk}=V(G)时,开路 C:P1P2P3…Pk-1PkP1称为图G的一条理想路,闭路C:P1P2P3…Pk-1PkP1称为图G的一个理想圈.如果图G有理想路,则称图G为理想图,如果图G有理想圈,则称图G为有圈图;若V(G)只有一个点,则图G(V,X)是平凡的.(注:本文不讨论平凡图).
概念3设图G=G(V,X)是一个有向图,若任意 PiPj∈X,都有唯一一个实数 d(PiPj)与之对应,则称图 G 是赋值 d 的图,d(PiPj)称线 PiPj的值;又若对任意 PiPj∈X,都有 PjPi∈X,且 d(PiPj)=d(PjPi),则称图 G 是无向图.

概念5设H是图G中具有某一特征的路的(非空)集合,H中值最小的路称为的H最短路,其值记为d(H);H中值最大的路称为的H最长路,其值记为 m(H).
1.2 线值方阵的概念
定义 1设G=G(V,X)是赋值d的图,V中的 n 个点顺序为 P1,P2,…,Pn,记

称为赋值d的图G给定点的顺序P1,P2,…,Pn的一个线值方阵,简称图G的一个线值方阵,简记为A= (aij)n,aij称为 A 的第 i行第 j列元素,aij(i=1,2,…,n)称为A的主对角线元素,称n为A的阶.
显然有:
性质1若G=G(V,X)是赋值d的无向图,则其线值方阵 A= (aij)n是对称阵,即 aij=aij(i=1,2,…,n)
性质2设G=G(V,X)是赋值 d的图,若V中任意两互异点P1,P2都有唯一有向线P1P2,则图G的线值方阵A=(aij)n除主对角线元素外,其余所有元素是实数,此种图称为完全图.
定理1设n阶方阵A=(aij)n的主对角线元素都为*,其它元素为实数或为*,则A可看作某一个图G的一个线值方阵.
证设点集 V={P1,P2,…,Pn},线集 X={Pi给有向图 G=G(V,X)赋值:d(PiPj) =aij(PiPj∈X),则 A= (aij)n为赋值d的图G给定点的顺序P1,P2,…,Pn的一个线值方阵.
定义 2设赋值 d的图 G=G(V,X)给定点的顺序 P1,P2,…,Pn的线值方阵为 A= (aij)n,若 An中不同行、不同列的n个非*元素可以排成


就称它是A的一组最短圈元素.

证由性质1结论成立.
2 线值方阵的变换
2.1 等差变换

2.2 换法变换

2)B可看作线值方阵;
3)A有一组最短圈元素当且仅当B有一组最短圈元素,且 d(A)=d(B).
证 1)不难验证;
2)不妨设i0<j0,A为赋值d的图G给定点的顺序 P1,P2,…,Pi0,….Pj0,…,Pn的一个线值方阵,则B是赋值d的图G给定点的顺序P1,P2,…,Pj0,….Pi0,…,Pn的一个线值方阵;
3)由于图G不变且图G赋值不变,所以图G若有短理想圈,则的最短理想圈不变,故A有一组最短圈元素当且仅当B有一组最短圈元素,且
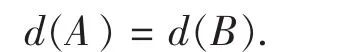
2.3 倍法变换
定理7(倍法变换) 若n阶线值方阵A=(aij)的每个非*元素都乘以同一个非负数k得到方阵B= (bij),记为 kA~B,则
1)B可看作线值方阵;
2)A有一组最短圈元素当且仅当B有一组最短圈元素,且 kd(A) =d(B).
证 1)设赋值d的图G=G(V,X)给定点的顺序 P1,P2,…,Pn的线值方阵为 A= (aij),对每个PiPj∈X,令 d′(PiPj) =kd(PiPj),则 G=G(V,X)也是赋值d′的图,此时B为赋值d′的图G给定点的顺序 P1,P2,…,Pn的一个线值方阵.

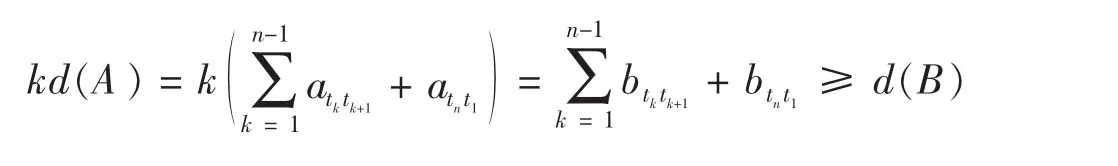

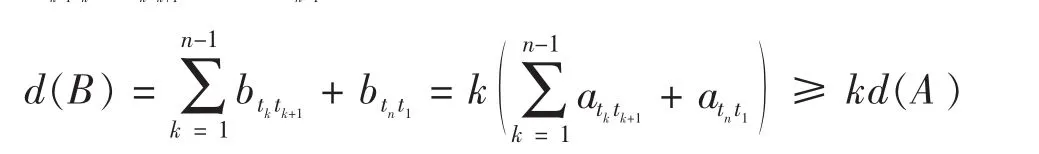
综上可知 kd(A) =d(B)而 at1t2,at2t3,…,atk-1tk,atktk+1,…,atnt1是A的一组最短圈元素当且仅当bt1t2,bt2t3,…,btk-1tk,btktk+1,…,btnt1是 B 的一组最短圈元素.
3 降阶定理
余方阵的概念及两个降阶定理在有向图的最短圈问题一文已给出[7],此不再论述.由第一降阶定理可得

4 最小圈值的估算
定理8 设A=(aij)为一个n阶线值方阵,A有圈,则

证设 a1t1,a2t2,…,aktk,…,antn是 A 的一组最短圈元素,则Λnaij≤ aiti,i=1,2,…,n.
j=1

定理9 设A是线值方阵,A中的非*元素非负,若d(A)≤ k,则A的任一组最短圈元素中不含有大于k的非*元素.

≤ k(i=1,2,…,n).
推论4 设A是线值方阵,A中的非*元素非负,将A的某一行(或列)中所有大于k的非*元素换为*得线值方阵 B,若 d(B)≤ k,则 d(A)=d(B).
推论5 设A是线值方阵,A中的非*元素非负,将A中所有大于k的非*元素换为*得线值方阵 B,若 d(B) ≤ k,则 d(A) =d(B).
定理 10设 A= (aij),B= (bij)为两个 n 阶线值方阵,A,B 的和方阵 C= (cij),(其中 cij=aijV bij,i,j=1,2,…,n),记为 AVB=C 则 C 为一个 n阶线值方阵,若C有圈,则A,B也有圈且
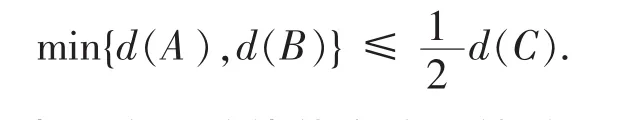


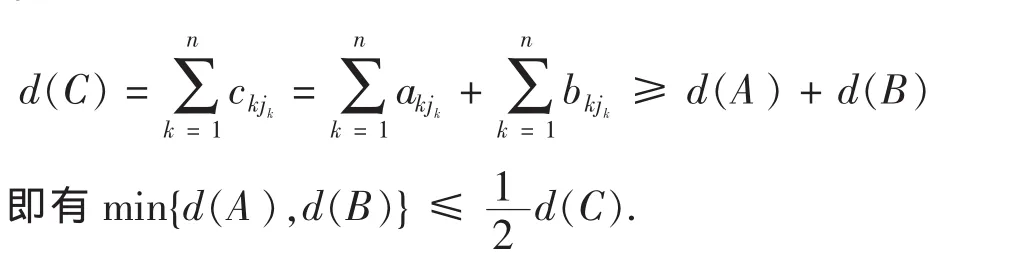

[1]马振华.现代应用数学手册:运筹学与最优化理论卷[M].北京:清华大学出版社,1997:276-277.
[2]潘玉奇,王潍,王永燕,等.货郎问题求解算法分析[J].济南大学学报:自然科学版,2002,16(4):336-339.
[3]廖春兰.货郎问题的近似解算法研究 [J].科技信息:科学教研,2008,24:41.
[4]徐海波.货郎担问题求解算法探讨 [J].山东省农业管理干部学院学报,2008,4:79-83.
[5][美]F.哈拉里著.图论[M].李慰萱译.上海:上海科学出版社,1980:77-80.
[6]黄文旭.货郎问题的算法[J].海南师范学院学报:自然科学版,1997,10(2):49-54.
[7]黄文旭.有向图的最短圈问题[J].海南师范学院学报:自然科学版,2000,13:33-37.
[8]黄文旭.货郎问题算法简介 [J].海南教育学院学报,1990(创刊号):89-94.
Transformation Methods of Square Matrix of Numerical Lines and Estimation of the Shortest Cycle Length
HUANG Wenxu
(College of Mathematics and Statics,Hainan Normal University,Haikou 571158,China)
The transformation methods of distance square matrix and the estimation of the shortest cycle length of directed graph are discussed in this article.As a result,we learn how to perform arithmetic transformation,exchange conversion and multiplier transformation of distance square matrix and find out the properties of these transformation methods.Moreover,a theorem for the estimation of the shortest cycle length of distance square matrix is deduced.
square matrix of numerical lines;transform algorithms;the shortest cycle length
O 157.5
A
1674-4942(2010)01-0004-04
2009-11-20
毕和平
