一种新的三角模糊数型层次分析法的排序方法

成先娟， 吉建华

（1.长江大学 信息与数学学院，湖北 荆州 434023；

2.广西财经学院 数学与统计系，广西 南宁 530003）

一种新的三角模糊数型层次分析法的排序方法

成先娟1， 吉建华2

（1.长江大学 信息与数学学院，湖北 荆州 434023；

2.广西财经学院 数学与统计系，广西 南宁 530003）

在层次分析法中，如何构造判断矩阵以及如何由判断矩阵导出被比较元素的相对排序权重是人们做决策时的一个关键环节.由于人类思维的复杂性及其模糊性，用模糊数来表示两元素的相对重要性更贴近实际，本文针对模糊数型的互补判断矩阵，提出了一种新的基于三角模糊数互补判断矩阵的排序方法.该方法计算量较小，易实现，且更贴近实际问题.

层次分析法；模糊数；判断矩阵；排序方法

层次分析法［1］（AHP）是一种定性与定量相结合的多准则决策方法，它将定性问题定量化，将复杂问题通过层次分解使整个决策过程更加科学化、民主化.随着AHP理论的发展和实际应用的需要，人们把模糊理论［2］引入到层次分析法中，模糊层次分析法便应运而生.

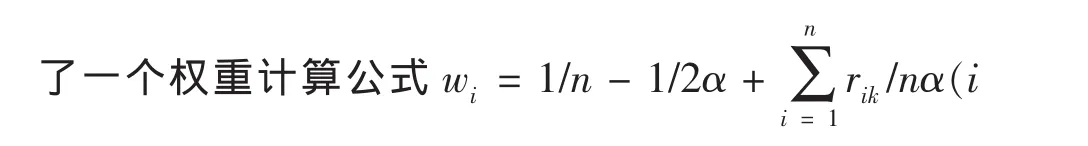
1 预备知识

由于客观事物的复杂性、不确定性及人类思维的模糊性，决策者往往很难给出明确的判断.在这种情况下，决策者往往只能给出事物间的模糊判断.如果根据所选标度将模糊判断转化为模糊数的形式，记为

现考虑在一个有限的决策方案集（或指标集）X={xii∈I}中选择最优方案或进行方案排序（xi表示第i个方案），决策者针对方案集X提供的信息，可由一类用三角模糊数表示的模糊判断矩阵给出.

设有判断矩阵 R= （rij）n×n，其中元素 rij表示相对于某个准则而言方案xi优于方案xj的程度.当判断矩阵的元素为三角模糊数，称此判断矩阵为三角模糊数判断矩阵.

定义1 实数集R上的模糊数M称为三角模糊数，如果其隶属函数为

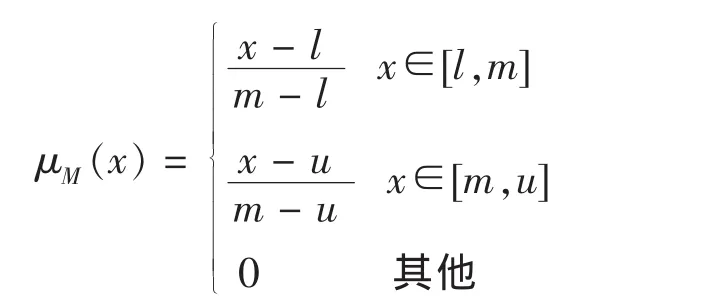
式中l，m，u为实数，且满足 l≤ m ≤ u，当 l=m=u时，M退化为非模糊数.

一般地，三角模糊数可记为 M= （l，m，u），有关三角模糊数的运算法则如下：

Lee和Li［5］借助于模糊事件概率测度的概念定义了模糊集的均值和标准偏差，对于服从均匀分布的情形，给出了三角模糊数均值和标准偏差的计算公式.设有三角模糊数A= （a，b，c），其均值为 m（A） = （a+b+c）/3，标准偏差为 σ2（A） = （a2+b2+c2-ab-ac-bc）/18.

三角模糊数的加、减、乘、除等运算是三角模糊数判断矩阵推导模糊权重的基础.

定义2［6］称三角模糊数判断矩阵R=（r）

ijn×n为三角模糊数互补判断矩阵，如果∀i， j∈I，rij＝ （rij，mij，uij），rji＝ （lji，mji，uji）为三角模糊数且满足：

2 一种三角模糊数互补矩阵的排序方法

比较常见的互补判断矩阵的排序方法有：姜艳萍、樊治平［6-7］基于可能度和期望值理论提出的两种排序方法；徐泽水［8-10］提出的基于可能度的排序方法、线性目标规划算法和基于FOWA算子的排序方法；马哓燕［11］提出的带概率的三角模糊数判断的排序算法等.在一定程度上，这些方法都能给出方案间的优劣次序，但都存在不足之处：如果专家所给的模糊数矩阵的一致性［12］较差，则所求的模糊数权重向量不能正确反映矩阵的判断信息，因此应该对判断矩阵进行一致性检验.

张吉军［4］从方法的科学性和可行性角度出发论证了文[13]提出的排序方法是目前最好的排序公式，文[14]是对文[15]方法的一种改进.

下面给出一种新的由三角模糊数判断矩阵的导出权重的排序方法，求解过程如下：

决策者针对方案集 X={x1，x2，…，xn}，可用三角模糊数表示方案两两比较的判断值，得到模糊数矩阵，权重向量为 V={v1，v2，…，vn}.

步骤 1如果矩阵R=（rij）n×n不是一致或满意一致的（用文[13]给出的模糊数互补矩阵加性一致的判别法检验），则对它进行调整；否则转下一步.

步骤 2由 R= （rij）n×n计算方案 xi（i∈I）的模糊数权重vi，根据三角模糊数的加法原理，得出权重的计算公式：

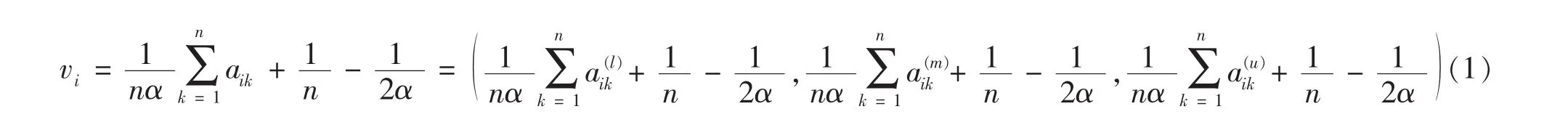
参数α=n/2-β+ε，β为判断矩阵R的最小行和的均值，可取ε=0.1或适当选取使得权重向量中的元素全为非负数.

步骤4根据排序指标R（vi）（i∈I）对方案进行排序，R（vi）越大其对应的方案越优.

3 算例分析

为了说明计算过程，给出了一个由三角模糊数互补判断矩阵导出方案排序的具体求解过程.设某决策问题由4个备选方案构成方案集Xi（i=1，2，3，4），某个专家给出的三角模糊数互补判断矩阵为

步骤1 经过调整后得到的满意一致矩阵为：

步骤2 取ε=0.27（使得计算出的权重全为非负）

1）根据三角模糊数的加法原理，求调整后的判断矩阵的行和ri和其均值m（ri）；

由上面的计算结果得β为行和的最小均值，β=m（r3） =1.42，α =0.85

2）根据公式（1）计算权重向量为 V={v1，v2，v3，v4}

v1= （0.232，0.353，0.474）

v2= （0.144，0.25，0.444）

v3= （0，0.176，0.353）

v4= （0，0.206，0.353）

步骤 3求排序指标 R（vi）（i=1，2，3，4）

R（v1） =0.391 R（v2） =0.261

R（v3） =0.243 R（v4） =0.277

步骤 4根据排序指标 R （vi）（i=1，2，3，4）对方案进行排序，R（vi）越大其对应的方案越优.

所以，方案1最好，其次是方案4，方案3最差.

4 结语

本文提出了一种更为贴近实际的新的决策方法，该法是在文[13]和[14]的基础上，进一步丰富了模糊数层次分析法的排序理论，而且ε越小表明决策者越重视元素间重要程度的差异，最后给出了一个由三角模糊数互补判断矩阵导出方案排序的具体求解过程.

［1］Saaty T L.The Analytic Hierarchy Process[M].NewYork:McGraw-Hill,1980.

［2］胡宝清.模糊理论基础[D].武汉:武汉大学出版社,2004.

［3］Van P J M,Laarhoven W Pedrycz.A Fuzzy extension of Saaty's priority theory[J].Fuzzy Sets and Systems,1983(11):229-241.

［4］张吉军.模糊一致判断矩阵3种排序方法的比较研究[J].系统工程与电子技术,2003,25(11):1370-1372.

［5］李荣钧.模糊多准则决策与应用[M].科学出版社,2002.

［6］姜艳萍,樊治平.三角模糊数互补判断矩阵排序的一种实用方法[J].系统工程学报,2002,20(2):89-92.

［7］姜艳萍,樊治平.一种三角模糊数互补判断矩阵的排序方法[J].系统工程与电子技术,2002,24(7):34-36.

［8］徐泽水.三角模糊数互补判断矩阵的一种排序方法[J].模糊系统与数学,2002,16(1):47-50.

［9］徐泽水.三角模糊数互补判断矩阵排序方法研究[J].系统工程学报,2004,19(1):85-88.

［10］徐泽水.基于FOWA算子的三角模糊数互补判断矩阵排序法[J].系统工程理论与实践,2003,23(10):86-89.

［11］马晓燕.带概率三角模糊数互补判断矩阵的一种简化排序方法[J].山东农业大学学报:自然科学版,2003,34(4):565-567.

［12］侯福均,吴祈宗.模糊数互补判断矩阵的加性一致性[J].北京理工大学学报,2004,24(4):365-369.

［13］吕跃进.基于模糊一致矩阵的层次分析法的排序[J].模糊数学与系统,2002,16(2):79-85.

［14］Zeng X l,Gong Y d,Cheng X j.Improvement of Priority Method for Fuzzy Complementary Judgement Matrix[A].2005 IEEE International Conference on Granular Computing[C]，2005:704-707.

［15］Cheng C H.A new approach for ranking fuzzy numbers by distance method[J].Fuzzy Sets and Systems,1998(95):307-317.

A New Priority Method of the Triangle Fuzzy Analytic Hierarchy Process

CHENG Xianjuan1，JI Jianhua2

（1.College of Mathematics and Information，Yangtze University，Jingzhou 434023，China；
2.Department of Mathematics and Statistics，Guangxi University of Finance and Economics，Nanning 530003，China）

In the analytic hierarchy process,it is a key step how to establish judgment matrices and get priority vectors from it.But due to the complexity and fuzzy of human thinking,it is practical to express the ratio of correlative weight with fuzzy number.This paper presents a new priority algorithms based on the triangle fuzzy complementary judgment matrix.Its superiority lies in the smaller computation and easier implement.It is even more closer to the actual problem.

Analytic Hierarchy Process；fuzzy number;judgment matrix;priority method

TD 851

A

1674-4942（2010）01-0008-04

2009-11-20

长江大学硕士科研启动基金(801070010107)

毕和平