基于地形熵的地形适配区选择准则研究*
2010-12-07席雷平陈自力李小民
席雷平,陈自力,李小民
(解放军军械工程学院,石家庄 050003)
0 引言
地形匹配导航作为一种高精度的自主导航方式,被广泛运用于飞行器等武器装备上,大大提高了武器系统的作战效能。然而,在地形匹配导航系统中,导航精度在很大程度上取决于地形的独特性(适配性),所以地形适配区的选择至关重要。文中从熵的概念入手,利用高程信息给出地形熵的定义,提出了基于地形熵的地形适配区选择准则,并在生成的DEM数字地图的基础上,对该适配区选择准则进行了仿真,结果表明该准则具有较好的地形适配区选择性能。
1 地形熵的定义
自从香农将物理中熵的概念引入到信息论以来,熵已被广泛应用于信号处理、图像处理等各种领域。设某信息源中包含的符号si有q个,相应的出现概率为P(si)。如果该信息源中符号序列的长度为N,当N较大时,该符号序列中出现符号si的个数为NP(si)个,出现NP(si)个si符号共得到的信息量为-NP(si)logP(si)。那么N个符号全部的信息量为:I= -NP(s1)logP(s1)- … -NP(sq)logP(sq)=
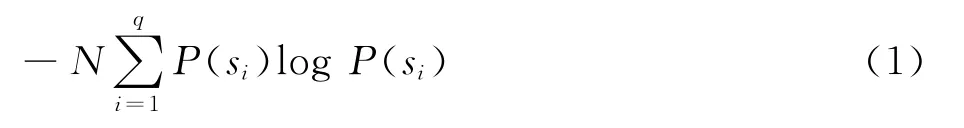
平均每个符号的信息量为:
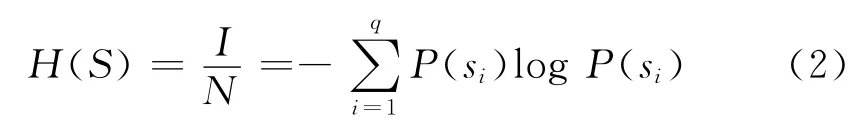
由式(2)可知,当q个符号出现的概率相差较大时,其熵值较小,反之,熵值较大。当q个符号等概率出现时,H(S)=logq,这时熵为最大值。因此熵反映了信息源中所包含的平均信息量的大小。
地形匹配导航所利用的是地形的高程信息,地形的起伏、变化及光滑程度等特征主要通过高程信息的变化来体现。不同地形区域内的高程分布规律是不同的,所以其包含的信息量也不同,起伏变化较大的地形包含了较多的信息量,而起伏变化较小的地形包含的信息量则较少,作为反映地形特征的高程数据也可以用熵来进行衡量,称其为地形熵。文中基于此考虑提出了基于地形熵的地形适配区的选择准则。
2 基于地形熵的适配区选择准则
假定匹配模板的大小为M×N(格网),模板中心格网点的坐标为(m,n),任意一点(i,j)的高程为h(i,j)(见图1)。
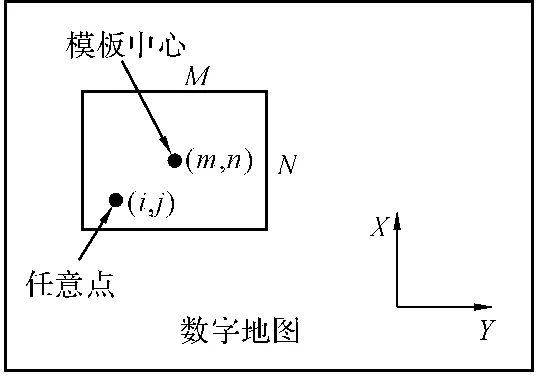
图1 匹配模板与数字地图
假定地形高程均为正值(有负值时可以统一加上一正数),由此定义局部地形熵为:
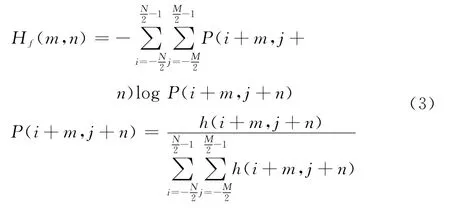
式中Hf为局部的地形熵。由于上式定义的局部地形熵在计算时涉及对数运算,计算量比较大,为简化计算,可利用泰勒展开得到如下的近似公式:
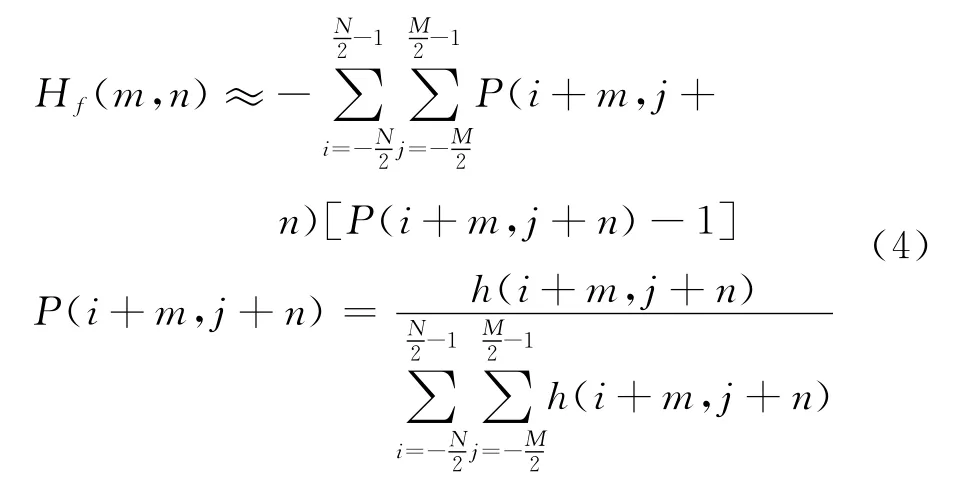
在计算局部地形熵的基础上,采用逻辑函数G来定义地形适配区的判决准则:
式中,HT为局部地形熵的阈值,可根据实验来测定。
根据局部地形熵来进行适配区选择具有以下特点:
1)局部地形熵反映了地形所含有信息量的大小,因此局部地形熵可描述地形的性质。如果某局部区域高程值变化越急剧,起伏变化越大,地形越独特,则计算出的局部地形熵就越小;否则,计算出来的地形熵就大。所以熵小的区域,适合作为匹配区域。
2)地形熵具有剔除离散点的作用。从局部地形熵的定义中可以看到:如果地形在小的范围内存在离散点(即奇异点),由于地形熵的大小依赖于整个局部地形区域的高程值,单个数据点的高程值对地形熵的影响很小,所以局部地形的地形熵变化较小。
3)因为熵对一定程度的基准误差是不敏感的,所以用局部地形熵来选择适配区具有良好的抗基准误差能力。对一组平均值为770.6m的200个地形高程数据计算地形熵后发现,在原来高程的基础上对每个地形高程数据增加100m,其平均高程变化了12.98%,而地形熵值从原来的2.30095变到了2.30097,只变化了0.01%。
3 实验仿真
在给出适配区选择准则的基础上,文中进行了大量的仿真实验,实验结果表明只要选取合适的地形熵阈值,该准则总能得到较好的地形适配区域。选取DEM数字地图中的一块区域来进行仿真,其大小为90×50(格网),格网间距为50m,图2是该区域对应的三维地形起伏图。
该地形区域所对应的等高线如图3所示。
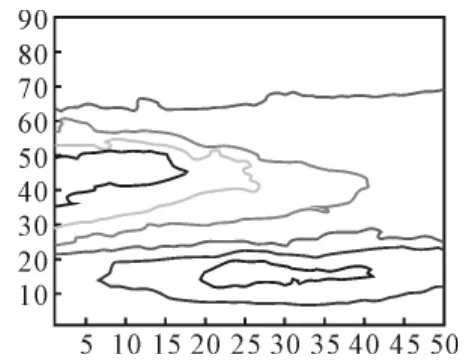
图3 地形的等高线图
在所选地形区域的基础上,取匹配模板窗口大小为20×20(格网),采用传统的基于地形统计参数的选择准则得到的适配区域
如图4中黑色部分所示(系统总噪声标准差σN取15m)。而采用基于地形熵的选择准则得到的适配区域如图5中黑色部分所示(地形熵的阈值取为9.286时)。
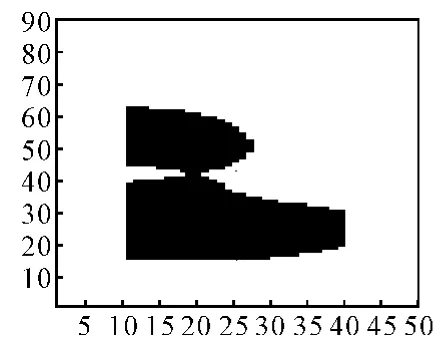
图4 基于地形统计参数准则得到的适配区域

图5 基于地形熵准则得到的适配区域
比较图4和图5,发现两种准则得到的适配区域基本相同,说明了文中所提出的基于地形熵的适配区选择准则具有较好的适配区选择效果。
[1]张祖勋.数字摄影测量学[M].武汉:武汉测绘科技大学出版社,1997.
[2]李志林.数字高程模型[M].武汉:武汉大学出版社,2007.
[3]朱继文.基于影像匹配数据获取DEM方法探讨[J].黑龙江工程学院学报,2009,23(1):36-38.
[4]王华.基于地形熵和地形差异熵的综合地形匹配算法[J].计算机技术与发展,2007,17(9):25-27.
[5]王伟.一种改进的地形熵匹配导航算法[J].计算机仿真,2007,24(2):11-13.
