朱载堉《论准徽与琴徽不同第十》释解评述

张志庄

(焦作师范高等专科学校 音乐系，河南 焦作 454001)

朱载堉《论准徽与琴徽不同第十》释解评述

张志庄

(焦作师范高等专科学校 音乐系，河南 焦作 454001)

通过对古琴徽位及律准徽位排列方法的解读，评述了朱载堉折纸取徽、古琴长度考辨、仲吕与十徽错位等问题。运用现代数学计算方法和公制度量，诠释了朱载堉算盘计算法及古度量尺寸，探讨了古琴徽位及律准徽位排列的律制方法。

律准；准徽；琴徽；折纸取徽

一、琴徽布徽法考辨

《论准徽与琴徽不同第十》载于朱载堉(以下简称朱氏)《律学新说·卷一·十章》。朱氏开言即将琴的第七徽与准的第一徽定位于中，其论如下：

准以琴第七徽之位为第一徽，自此之右无徽，自此之左十二律吕皆有徽矣。此二者大不同，然各有理存乎其中。盖琴家自岳山至龙龈二者间，用纸一条，作为四折，以定四徽、七徽、十徽；作为五折，以定三徽、六徽、八徽、十一徽；作为六折，以定二徽、五徽、七徽、九徽、十二徽。首末两徽乃四徽折半也。此法最为简易。若以算法定之，则置琴长若干为实，四归得四徽，一倍即七徽，二倍即十徽也。五归得三徽，一倍即六徽，二倍即八徽，三倍即十一徽也，六归得二徽，一倍即五徽，二倍即七徽，三倍即九徽，四倍即十二徽也。八归得一徽，七因之即十三徽也。准徽则异于是[1]71。

朱氏将准徽位以琴的第七徽为第一徽，古琴七徽则定于折纸法的二分之一处。据此可知，准的第一徽位应在准的岳山和龙龈正中。第一徽至右无徽位，至左分别排列十二徽位。琴徽与准徽二者徽位排列虽不同，但各有道理在其中。古琴徽位排定方法，朱氏采用的是折纸法，即把与琴弦同长的纸条依次折为二、三、四、五、六、八等分，取其“折”点为徽位，以琴面正中即二分之一处为中心(七徽)，两边对称并以三、四、五、六、八等分设徽，所定徽位在岳山至龙龈之间，用纸一条，先折四折，正中间一折为七徽，其余两折为四徽和十徽，折成五折，可定三徽、六徽、八徽、十一徽；折成六折，可定二徽、五徽、七徽、九徽、十二徽。首末两徽即一徽、十三徽，采用四徽折半即可得。若以算法定徽，以琴长四尺五寸为实，“四归”即将整体弦长分四份，置琴龙龈至岳山为四尺五寸，除以四即得四徽一尺一寸二分五厘，一倍即用四尺五寸除以四的商乘以二，二倍即用四尺五寸除以四的商乘以三，余倍类推。五归即用四尺五寸除以五，六归即四尺五寸除以六，八归即四尺五寸除以八，“七因之”即四尺五寸除以八的商乘以七得十三徽三尺九寸三分七厘五毫。为直观起见，根据朱氏原文，以古度尺琴长四尺五寸为例，将上文用现代数学计算方法计算，结果见表1。

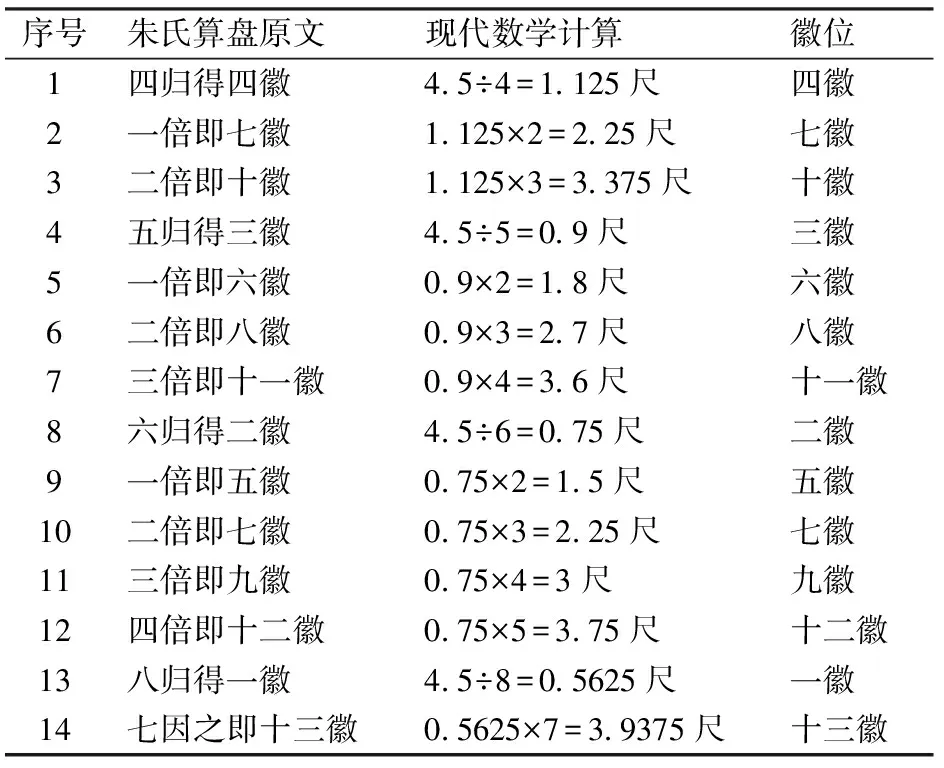
表1 朱氏算盘原文与现代数学计算方法

朱氏所言四折取中折纸法，是关于古琴泛音徽位定弦法的高度理论概括，源于南宋朱熹(1130-1200年)的《琴律说》。琴徽即古琴上的徽位，是区别于其他乐器的唯一标识。琴徽产生的年代目前尚有争议，但就目前所知，最早记载琴徽的文献是魏晋时期嵇康(224-263年)的《琴赋》，其中有“弦以园客之丝，徽以钟山之玉”，“弦长故徽鸣”等句。它既证明了当时已有徽位，还说明了古琴上的十三个徽位是按照能在琴上奏出泛音的相应位置来设定的。

由朱氏所论及表1数据可知，古琴十三徽是按照岳山至龙龈间琴弦的二、三、四、五、六、八等分的节点来设置的；因此，无论琴长是否一致，其十三徽各徽所示的弦长比例是不变的，亦可说古今不同长度琴上所奏出的相对音高关系应该是一致的。十三徽泛音的音高是以七徽为中心，两边呈对称状态，八徽同六徽，九徽同五徽，十徽同四徽，十一徽同三徽，十二徽同二徽，十三徽同一徽，其弦长比值是相同的。其中，三、六、八、十一徽上的泛音音高也是相同的。之所以呈现此种状况，是由于泛音取弦长分段振动(弦的二分之一、三分之一……)所致。根据朱氏所论及各徽位尺寸排列(表2)[2]384，可清楚地看出其弦长比值。

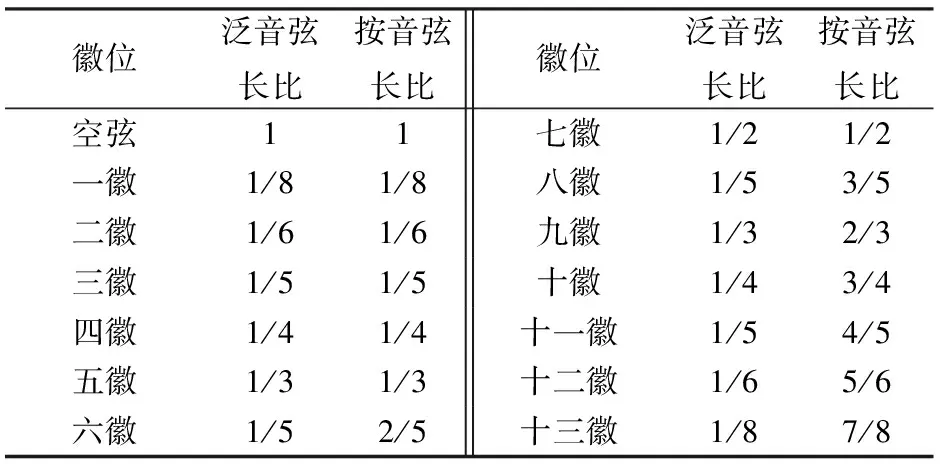
表2 各徽位尺寸排列

二、古琴、律准长度比较考辨

朱氏《律学新说·卷一·九章》对律准作了详尽的考证和数度考辨，尤其对琴、准尺度、徽位的比较考辨更是前无古人，其论如下：

风俗通曰：琴长四尺五寸，法四时五行也。后汉志载，京房所制律准，隐间九尺，以应黄钟，此乃琴之类耳。四尺五寸乃九尺折半之数。是故黄钟九尺，在准则其隐间九尺，在琴须折半，故龈岳中间为四尺五寸。太史公谓琴长八尺一寸，以九寸之尺约之，亦是九尺，与京氏之说合。谨按先儒言琴尺度，惟有二家最当。其一说云：律之九寸也，数之八十一也，琴之八尺一寸也，三者之相与固未嘗有异焉。今以琴之太长而不适于用也，故十其九而为九尺，又折其半而为四尺五寸，则四尺五寸之琴与夫九寸之律、八十一之数，也未始有异也。此朱熹之说，见于经世大训。又一说云：琴体分为三准，自一徽至四徽谓之上准，上准四寸半，以象黄钟子律。自四徽至七徽谓之中准，中准九寸，以象黄钟之正律。自七徽至龙龈谓之下准，下准一尺八寸，以象黄钟之倍律。三准各具十二律，声按弦附木而取。然须转弦，合本律所用之字，若不转弦，则误触散声，落别律矣。每一弦各具三十六声，皆自然也。此姜夔之说，见于文献通考。二家所说，琴制长短实同，而尺寸之数则有不同，乃所用之尺为异耳。姜氏尺寸皆依曲尺，以曲尺是鲁般(班)所造，百世不易，为真古尺。故琴书曰：伏羲作琴长三尺六寸，法期之数，古之制也。朱子却依黍尺为之，盖黍尺之一尺，即曲尺之八寸，故彼曲尺三尺六寸，与此黍尺四尺五寸正合。夫龈岳中间发声之处，长五九四十五寸者，象洛书之积数，其长四九三十六寸者，象老阳之策数，除龈、岳、额、尾在外也。其说卓矣。今从朱子之说，广其未备者耳[1]72。

《风俗通》即《风俗通义》，是东汉学者应劭[3](153-196年)所著。琴的长度四尺五寸，其“四”象征春、夏、秋、冬，“五”象征金、木、水、火、土。《后汉志·律历上》记载了京房[4]所制律准，隐间九尺，以应黄钟。隐间是指龙龈至岳山之间的长度(即弦振动部分的实际长度)，九尺所指为律准之长度，朱载堉评曰“此乃琴之类耳”。四尺五寸是九尺之半，故黄钟九尺有误。《后汉书》所载为“黄钟九寸”，朱氏在此可能是指九寸黄钟数度。以准而论，其隐间为九尺；以琴而论，则应折半。所以，古琴从龙龈到岳山中间应为四尺五寸。《史记·乐书》记载，琴长八尺一寸，是以九寸之尺而言，九九八十一寸，亦是九尺，与京房所说相同。按先儒所言琴的尺度，只有两家最得当。其一说律之九寸，数之八十一，琴之八尺一寸，三者相同无异。现因琴体太长而不适于演奏，所以十其九为九尺，又折一半为四尺五寸，则四尺五寸之琴与九寸之律、八十一之数亦相同，此为朱熹之说。第二种说法指琴体分为三准(准，即具备五音十二律)，从一徽到四徽称为上准；上准四寸半，岳山至四徽的长度，以像黄钟的高八度律。从四徽至七徽称为中准(实际是岳山至七徽的长度)，中准九寸，以像黄钟的正律。从七徽至龙龈称为下准，下准一尺八寸，以像黄钟的低八度律。三准各具五声十二律，声音按弦压到贴着琴面板而取。但需要换弦，才合本律所用之音。若不换弦，则误触散声，则鸣的是别的律了。每一弦可奏出三十六音，皆为自然之音，此为姜夔[5](1155-1221年)之说。两家所说琴的长短实际是相同的，而尺寸之数的不同，是因为所用尺的不同。姜夔所用之尺与明朝曲尺相同，曲尺是鲁班所造，百世不变，为真正的古尺。所以，《琴书》说伏羲制作的琴长三尺六寸，其数为古制。朱氏却是以黍尺而作琴，而黍尺的一尺相当于曲尺的八寸，所以伏羲的三尺六寸与朱氏的四尺五寸是一样的长。龙龈至岳山之间发声之处，长四尺五寸，像洛书的积数(1+2+3……+9=45)，其长四九三十六寸，像易经像数的老阳之数。现依朱熹之说，将各徽位古度尺与明曲尺对比分析如下：

其一，古琴长度在中国古代是各不相同的，朱氏说《风俗通》所载之琴、汉京房所载之琴及太史公之琴是具有代表性的三种尺度，其实际长度是相等的，但此说不一定准确。据古代文献记载，历代琴制有八尺一寸、七尺二寸、四尺五寸、三尺六寸六分等多种不同的长度。但是，古琴上的徽位总是按照龙龈至岳山之间的长度比例设置的；因此，不论琴的长短，第七徽总是在全弦振动的二分之一处，第四徽总是在全弦震动的四分之一处，其他诸弦亦成类似的比例。这样，无论琴长若干，其徽位排列比例、弦长振动比例与音高却是相同的。北宋科学家沈括(1031-1095年)对此已有精辟论述，其《梦溪笔谈·补笔谈》说：“所谓正声者，如弦之有十三泛韵，此十二律自然之节也。盈丈之弦，其节亦十三；盈尺之弦，其节亦十三。故琴以为十三徽。不独琴如此，金石亦然。”沈括认为，弦上发泛音之处便是自然之节，是“天地至理”，人不能以毫厘损益“自然之节”上所发出的声音。不论是一丈多长的琴，还是一尺多长的琴，其节点都是十三节(十三徽位)。

其二，朱氏的“琴体分为三准”之说载于《宋史·卷124·志95·乐17》，文中有“姜夔乐议分琴为三准”之论。其中三准论前的琴律论述，源于朱熹《琴律说》。《琴律说》是研究我国七弦琴音律的专门著作，朱熹在论著中对当时七弦琴按徽位、取按音以及在第十三徽外取徽外音作了律学上的实践。其文为：“盖初弦黄钟之宫，次弦太簇之商……皆起于龙龈，皆终于临岳，其长皆四尺五寸，是皆不待抑按，而为本律自然之散声也。而是七弦者，一弦之中又各有五声十二律者凡三焉。且以初弦五声之初言之，则黄钟之律固起于龙龈而为宫声之初矣。太簇则应于十三徽之左而为商，姑冼则应于十一徽而为角。林钟则应于九徽而为徵，南吕则应于八而为羽……若七徽之后以至四徽之前，则五声十二律之应，亦各于其初之次而半之。”朱熹所论，清楚地表明了一条琴弦上的上、中、下三准三组五声音阶的按音音位。如将朱熹所论转化成表3[2]386，可更清晰地明辨朱氏所论三准之说。

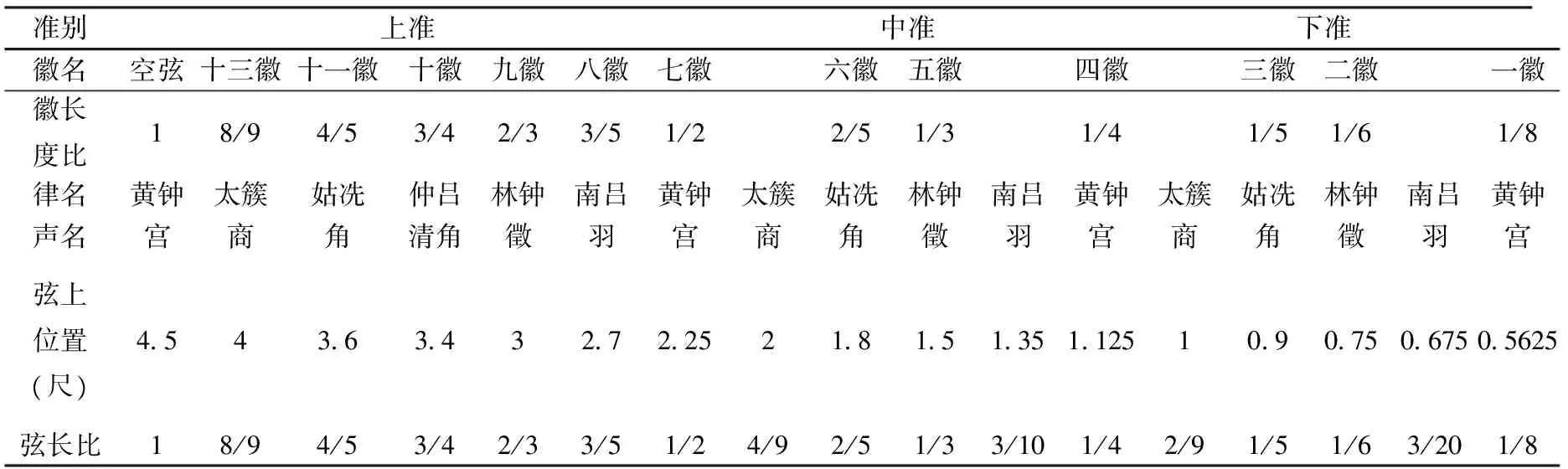
表3 上、中、下三准三组五声音阶按音音位

三、各徽位古度尺、明曲尺及现代度量考辨

以古度一尺等于明曲尺八寸为根据，朱氏对古琴徽位排定作了详细的考辨。第一徽，古度尺五寸六分二厘半，今曲尺四寸五分；第二徽，古度尺七寸五分，今曲尺六寸；第三徽，古度尺九寸，今曲尺七寸二分；第四徽，古度尺一尺一寸二分半，今曲尺九寸；第五徽，古度尺一尺五寸，今曲尺一尺二寸；第六徽，古度尺一尺八寸，今曲尺一尺四寸四分；第七徽，古度尺二尺二寸五分，今曲尺一尺八寸；第八徽，古度尺二尺七寸，今曲尺二尺一寸六分；第九徽，古度尺三尺，今曲尺二尺四寸；第十徽，古度尺三尺三寸七分半，今曲尺二尺七寸；第十一徽，古度尺三尺六寸，今曲尺二尺八寸八分；第十二徽，古度尺三尺七寸五分，今曲尺三尺；第十三徽，古度尺三尺九寸三分七厘半，今曲尺三尺一寸五分[1]72-73。龙龈距岳古度尺四尺五寸，今曲尺三尺六寸。根据古度一尺等于明曲尺八寸，一曲尺等于现代公制31.56厘米的换算法，可将三种度量用表4表示。

四、定弦法、仲吕徽位及“徽”字解

琴徽位排定之前需要准确量测各徽之间的数度，因徽位本身有一定的数度，故量测时应以徽中为准。朱氏原文如下：

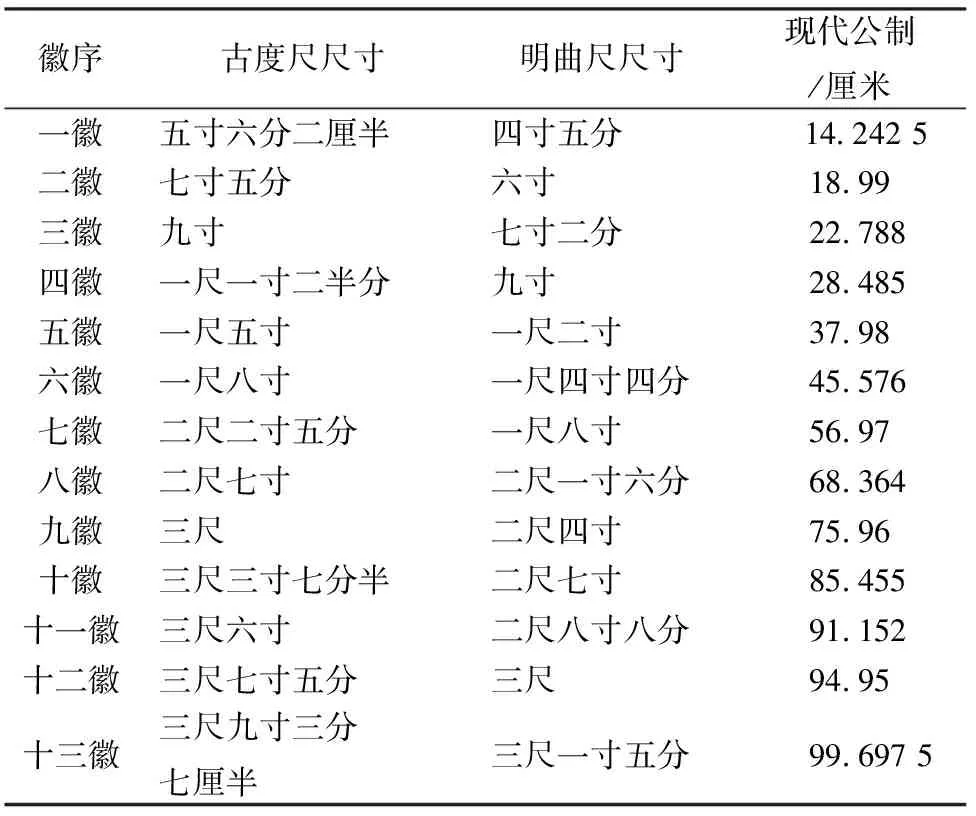
表4 古度尺、明曲尺、现代度量换算

凡量琴徽，须自临岳量至本徽中心为止，方是正音之位，切勿量至徽边而止也。量次徽亦然，从徽中心量起，勿从徽边量也。或问：凡琴定弦，专取九徽、十徽，不取余徽何也？答曰：九徽、十徽琴之纲领，调弦考律必先较之，乃天地自然之音，非人力所能为也。于此两徽考之，方知新旧二种算术孰为疏密。且见仲吕正位不与十徽对者，非也。问曰：律位既不对徽，移徽以就律位可乎？答曰：不可也。琴中有徽，辟犹天之赤道，徽间有律。辟犹日之黄道。圣人制作，各主一理，并行而不相悖。大雅云：太姒嗣徽音，徽之为言美也。琴家取名，盖本诸此。七徽分中，而左右各六，虽有远近，而左右相对。当徽之处，泛音则鸣，否则不鸣，此所以为美也。陈暘改为光晖之晖，谬也。今若移徽就律，虽则实音不差，而左右疏密不相对，岂得成徽也哉！先儒嘗有移徽就律之说，盖亦未之思欤！今将新旧二法所算尺寸，具载于此，以俟后世明理善数之士，将此说与琴音校定，审而辨之，则真理自见矣[1]72-74。

(1)古琴岳山至龙龈与各徽位的测量方法问题。朱氏首先讲了量测琴徽必须从临岳量测至徽的正中，切不可量测至徽边而止。下推量测次一徽位，也要从徽中心量测起。为更清楚说明其定弦方法，朱氏采用了问答的形式。问：凡定琴弦，专取九徽、十徽，不取其余弦，这是为什么？答：九徽与十徽是琴的纲领，调弦考证音律必须首先校正之，因为九徽和十徽是天地自然之音，不是人力所能为的。朱氏所谓的天地自然之音和数，指的是河图(最大数为十)、洛书(最大数为九)的自然之数。九徽乃弦的三分之二处，十徽乃弦的四分之三处，如定一弦散声为黄钟(宫)，则九徽处的泛音则为林钟(徵)。朱氏所论方法源于朱熹《琴律说》，其定弦方法被描述为：“盖九徽之宫，隔二者生散徵，而散徵隔一上生十徽之商。九徽之商隔二下生散羽，而散羽隔一上生十一徽之角。九徽之角隔二下生散少宫，而散少宫隔一上生十徽之徵。九徽之徽隔二下生散少商，而散少商隔一上生十徽之羽也。”我国著名的律学家李玫将其释解为：一弦为宫，其九弦与相隔两弦的第四弦相应，四弦散声为徵；第四弦散声与相隔一弦的二弦十徽相应，二弦散声为商；二弦九徽与相隔两弦的第五弦散声相应，五弦散声为羽；五弦散声与相隔一弦的第三弦十一徽相应，三弦散声为角(清角)；三弦九徽与相隔两弦的第六弦散声相应，六弦散声为少宫；六弦散声与相隔一弦的第四弦十徽相应；第四弦九徽与相隔两弦的第七弦散声相应，七弦散声为少商；第七弦散声与相隔一弦的的五弦十徽相应，五弦散声为羽[6]。考较此二徽，才能知道三分损益律与密律算法哪一个更精确。

(2)仲吕正位不与第十徽相对的问题。朱氏的观点是肯定律位不必对准徽位的。在七弦琴上，如按旧法(三分损益法)计算，仲吕之音在十徽右0.454寸；按新法计算(十二平均律)，仲吕在十徽右0.038寸。七弦琴上有效震动弦长为准弦长折半四尺五寸，其仲吕有效振动弦长按三分损益律计算为45寸×3/4 -0.454=33.296寸，按十二平均律计算为45寸×3/4 -0.038=33.712寸，旧律与新律的误差为33.712寸-33.296寸=0.416寸。朱氏再设问作答：“律位既不对徽，移徽以就律位可乎？答曰：不可也。”对此，朱氏的解释为琴中之徽犹如天之赤道，徽间有律犹如日之黄道。上古圣人在制作之时各主一理，对应与不对应并行而不相悖也。朱氏引《诗经·大雅·思齐》“太姒嗣徽音”，朱氏对徽的解释为“美”。据朱氏所解“徽”即“美”，其道理为徽上之音是泛音，是透亮、纯净、优美之音。琴家对徽的起名即源于此。以第七徽为中心，左右各六徽，虽有远近之差，但左右相对。正徽之中，用左手轻抚徽位右手弹奏，泛音则鸣，否则不鸣，此即为美。宋代音乐理论家陈暘将徽改为光晖之晖，朱氏指其“谬矣”。如果移徽就律于泛音处，虽然按音不差，能出现泛音，但是左右的疏密不能相对，怎么能成徽位。先儒有移徽就律之说，是因为没有深思所致。为使后世善于数理且懂音乐之士明白此理，朱氏将新旧两种方法所算尺寸具载于后，并指出若将此说与琴音仔细较定、审而辨之，则真理自见。

朱氏言“见仲吕正位不与十徽相对”的问题，究其原因是律制问题。朱氏所算旧法为三分损益律制，新法密律为十二平均律制，而明朝以前古琴布徽定律是遵照自然之节而定，其律制据陈应时先生研究结果应为纯律[2]。从上述各表中可知，七弦琴十徽位置是在全弦长的3/4处，仲吕在此的音声为清角，也就是我们现代人所唱的fa。由此可知，朱氏在当时不一定知道古琴在明朝之前是以纯律为生律法则的，明、清以后的琴谱才倾向三分损益律的应用。

五、各律徽位新、旧计算方法及数度考辨

为推出新律，朱氏采用对比的方法，将三分损益律所算数据，与密律(十二平均律)所算数据进行了如下比较，以俟后世明理善数之士与琴音校定，审而辨之，则自见其真理。

律准旧法与新法的比较见表5[1]295-296。

黄钟律九寸，准九尺，折半四尺五寸(岳山至龙龈是也)。又折半二尺二寸五分(七徽是也)，旧在七徽右三分0二毫奇，新在正对七徽。大吕八寸四分小分三弱，准八尺四寸三分弱，折半四尺二寸一份三厘九毫奇。旧在十三徽左二寸七分六厘四毫奇，新在十三徽左三寸0九厘九毫奇。

太簇八寸，准八尺，折半四尺。旧在十三徽左六分二厘五毫整，新在十三徽左七分一厘五毫奇。

夹钟律七寸四分小分九微强，准七尺四寸九分微强，折半三尺七寸四分五厘七毫奇。旧在十二徽右四厘二毫奇，新在十二徽左三分四厘奇。

姑冼律七寸一分小分一微强，准七尺一寸一分微强，折半三尺五寸五分五厘五毫奇。旧在十一徽右四分四厘四毫奇，新在十一徽右二分八厘三毫奇。

仲吕律六寸六分小六分弱，准六尺六寸六分弱，折半三尺三寸二分九厘五毫奇。旧在十徽右四分五厘四毫奇，新在十徽右三厘八毫奇。

蕤宾律六寸三分小分二微强，准六尺三寸二分微强，折半三尺一寸六分0四毫奇。旧在九左一寸六分0四毫奇，新在九徽左一寸八分一厘九毫奇。

林钟律六寸，准六尺，折半三尺。旧在正对九徽，新在九徽左三厘三毫奇。

夷则律五寸小分二弱，准五尺六寸二分弱，折半二尺八寸0九厘三毫奇。旧在八徽左一寸0九厘三毫奇，新在八徽左一寸三分四厘八毫奇。

表5 律准旧法与新法

南吕律五寸三分小分三强，准五尺三寸三分强，折半二尺六寸六分六厘六毫奇。旧在八徽右三分三厘三毫奇，新在八徽右二分四厘二毫奇。

无射律四寸九分小分九强，准四尺九寸九分强，折半二尺四寸九分七厘一毫奇。旧在七徽左二寸四分七厘一毫奇，新在七徽左二寸七分五厘五毫奇。

应钟律四寸七分小分四微强，准四尺七寸四分微强，折半二尺三寸七分0三毫奇[1]75-78。旧在七徽左一寸二分0三毫奇，新在七徽左一寸三分三厘七毫奇。

六、结 语

朱氏《论准徽与琴徽不同第十》的目的有三：其一，在律准及七弦琴上进行旧律(三分损益律)与新律(十二平均律)的比较。除考证各律徽位的数据尺寸外，其真实意图在于推出新律。但朱氏所处时代尚无音分、振动频率之说，故朱氏所言的新、旧律制在中国明朝之前的七弦琴上并未使用，其徽位排列布法乃为纯律律制，所以出现了十徽与仲吕不相对的情况。其二，朱氏考证七弦琴长及律准长度，是为其新律准的推出做的铺垫和呼吁。中国历代度、量、衡的差异是一个非常复杂的问题，朱氏对新律与旧律进行的比较研究，实际上是在九与十进位制上所进行的算术思维。他创造了以算盘折算的简便方法，解决了纵黍律长九寸和横黍度长十寸换算的问题。这不仅在律学范围内前无古人，即便在世界数学史上，也是名列前茅的。其三，朱氏文化知识渊博，所引《易经》、《诗经》、《河图》、《洛书》、《史记》、《风俗通》、《后汉志》、《文献通考》、《琴书》、《经世大训》等，属多学科理论专著，所涉人物如伏羲、司马迁、京房、姜夔、朱熹、陈暘等均为历代名儒。由此可知，朱载堉以史家的气概，检阅、评说、总结了各种律学理论和资料，并吸收一切有益于新律构建的滋养，批评一切他认为妨碍他律学新说的障碍。

[1] 朱载堉．律学新说[M]．北京：人民音乐出版社，1986．

[2] 陈应时．中国乐律学探微[M]．上海：上海音乐学院出版社，2004.

[3] 范晔．后汉书[M]．北京：中华书局，2000：1085-1089．

[4] 班固．汉书·律历[M]．北京：中华书局，2000：2029．

[5] 脱脱，阿鲁图，铁木儿塔识，等．宋史[M]．北京：中华书局，2000：2235．

[6] 李玫．东西方乐律学[M]．北京：中央音乐学院出版社，2007：88．

[责任编辑 杨玉东]

InterpretationsandReviewsonZhuZaiyu’s“OntheDifferencesoftheQuasi-emblemandthe10thEmblemonGuqin”

ZHANGZhi-zhuang

(MusicDepartment,JiaozuoTeachersCollege,Jiaozuo454001,Henan,China)

Through the interpretation of the permutation method for the emblem arrangements and the quasi-temperament emblem arrangements on Guqin， the paper introduces the procedures of Zhu Zaiyu’s paper folding technique for the emblem arrangements on Guqin，distinguishing the length of Guqin and discussing the non-corresponding position of the Fa-tone with the 10th emblem on Guqin. By using the modern mathematical calculation method and the metric measurements, it explains Zhu Zaiyu’s abacus calculation method and the ancient measurements, researches the emblem position and the quasi-temperament arrangements on Guqin, interprets the contents of Zhu Zaiyu’s “On the Differences of the Quasi-emblem and the 10th Emblem on Guqin”.

quasi-temperament; quasi-emblem; emblem on Guqin; paper folding technique for emblem

2010-01-27

张志庄(1955-)，男，河南焦作人，教授，从事音乐教学和音乐理论研究。

E-mail：zhangzhizhuang321@163.com

J8

A

1673-9779(2010)02-0250-07