有限幂零群的两个充分条件＊

唐跃跃,郭继东

(伊犁师范学院,新疆 伊宁 835000)

有限幂零群的两个充分条件＊

唐跃跃,郭继东

(伊犁师范学院,新疆 伊宁 835000)

群的半直积是对直积的一种削弱,本文对半直积推广到n个群的形式,并利用半直积给出了幂零群的一个充分条件。对正规子群加强条件,定理3给出了幂零群的一个类似可解群的判定条件。

半直积;幂零群;有限群

在有限群中,幂零群是介于交换群和可解群的一类群,对有限群的构造起着非常重要的作用,幂零群可以分解成Sylow子群的直积。半直积是直积的一种削弱形式,本文对文献[1]定义的半直积对半直积进行了推广,并利用定理1推广到n个群的半直积得到了幂零群的一个充要条件。

另一方面,在有限群论中,人们常常利用G的正规子群N是可解的,且商群G/N也是可解来判定有限群G可解性。尽管幂零群一定是可解群,但是这一类似证明方法却不能用在幂零群中,即 N◁G,N是幂零的,且G/N也是幂零的,在一般情况下却推不出G是幂零的,例如文献[2]提到群G=S3,则G的真子群都是循环的,从而是群G的正规子群也是循环的,并且商群也都是循环的,但是群 G并不是幂零的。于是本文对正规子群N加强条件,得到了两个类似可解群判定的判定定理。

本文所涉及的群均为有限群,H＜G表示 H是G的真子群,N▷G表示N是G的正规子群,Sy lp(G)表示G的所有的Sylow p-子群所成的集合,其它未提及的术语及定义可参见文献[1]。

1 主要定义和引理

定义1[1]设 H,K为两个抽象群,a:k→A ut(H)是同态映射,则 H和 K关于a的G=H＞＜K规定为 G=H＞＜K={(x,a)|x∈H,a∈K}。

运算为:(x,a)(y,b)=(xy,ayb)。

设 K到A ut(H)的一个同态σ:h→σn,则σn是H的一个自同构,σn:k1→kh。由于σ是同态,所以σh1σh2=σh1h2。因此(kh1)h2=kh1h2。

注:由定义1中定义的G是一个群,称为 H和 K的半直积,记为G=H＞＜K证明可参见文献[3]。

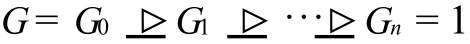
引理1[4](Frattini论断)设 N◁G,P∈Sy lp(N),则 G=NG(P)N。

引理2[4]设 H是有限群,则下述事项等价

(1)G是幂零的

(2)若 H＜G,则 H＜NG(H)

(4)G的每个Sylow子群都是正规的,从而G是它的Sylow子群的直积。

2 主要结果

定理1 设 Hi分别是群,令 G={(x1,x2,…xn)|xi∈Hi}

对∀(x1,x2,…xn),(y1,y2,…yn)∈G,

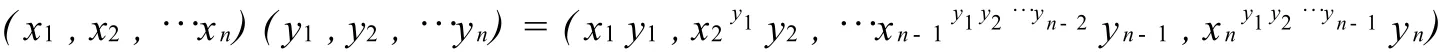
则 G为一个群,称为 H1,H2,…Hn的半直积,记为 G=H1＞＜H2＞＜…＞＜Hn

证明 根据定义显然满足乘法封闭。

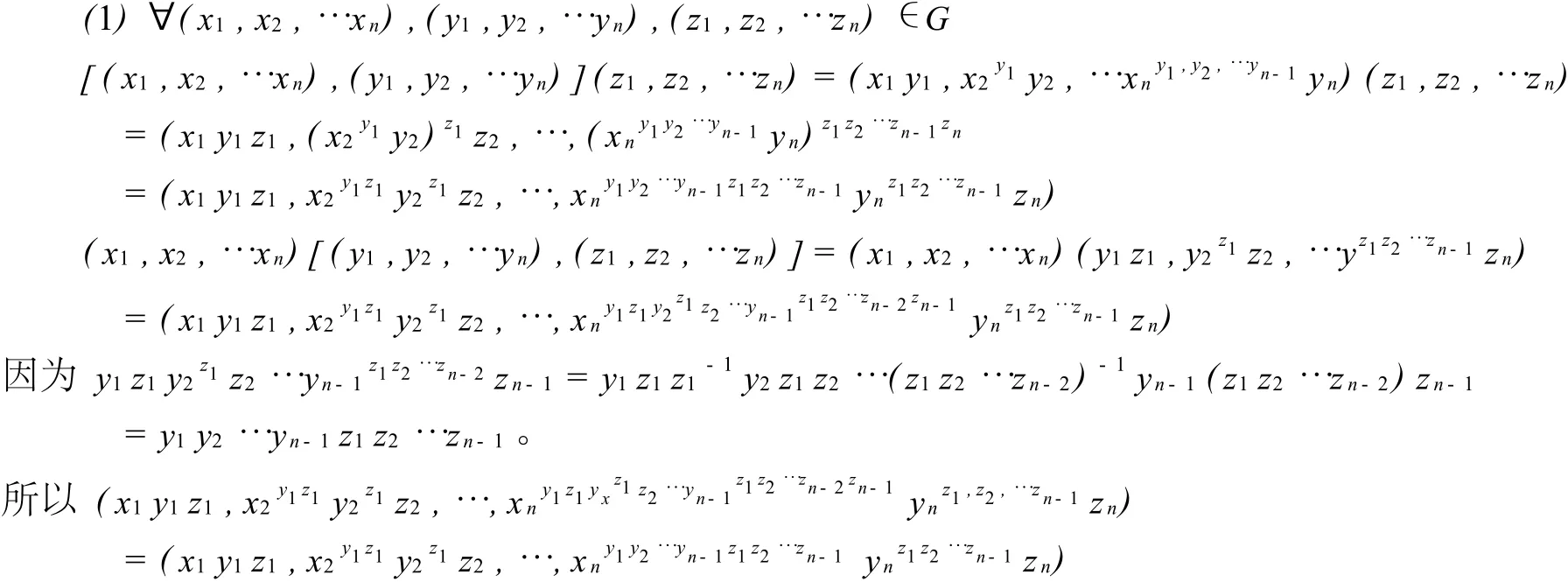
从而 [(x1,x2,…xn),(y1,y2,…yn)](z1,z2,…,zn)=(x1,x2,…xn)[(y1,y2,…yn),(z1,z2,…zn)]满足结合律。

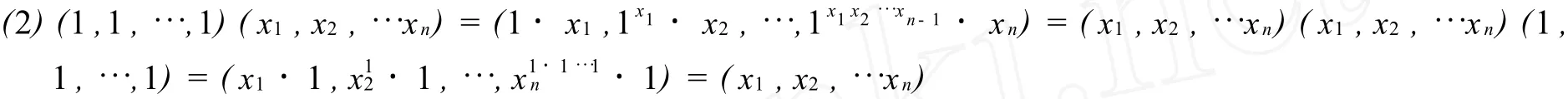
所以 (1,1,…,1)为G的单位元。

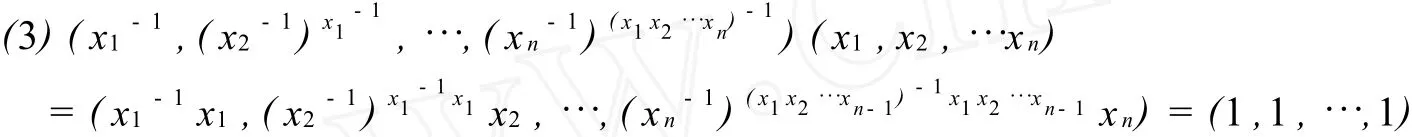
推论2 设群 G=G1＞＜G2＞＜…＞＜Gn,其中 Gi(i=1,2,…,n)是幂零的,则 G是幂零的。

定理2 群G是幂零的充要条件,是G可以写成幂零子群和幂零的正规子群半直积的形式。

证明 由推论2知充分性成立。

反之,若G是幂零的,从而 G可写成sylow子群的直积形式,直积显然是半直积,又由于每个Sylow子群都是 p-群,从而Sylow子群都是幂零的,则G可写成幂零子群和幂零正规子群的半直积形式。

定理3 若 Z(G)是极小正规子群,且 G/Z(G)是幂零群,则G是幂零群

[1]陈重穆.有限群论基础[M].重庆:重庆出版社,1983:33-35.

[2]张远达.有限群构造[M].北京:科学出版社,1982.

[3]王萼芳.有限群论基础[M].北京:北京大学出版社,1985:148-163.

[4]徐明曜.有限群导引:上册[M].北京:科学出版社,1999.

[5]刘仕田,黄喻.半直积与有限群的幂零[J].贵州科学,2006,12(4):18-19.

[6]李方方,曾洪平.子群的性质对有限群结构的影响[J].西南大学学报,2008,8(8):5-8.

[7]Hall M.Theo ry of groups[M].New York:Macmillan,1959.

(责任编辑:刘乃生)

2009-12-10

新疆高等学校科研计划项目(XJEDU 2005E06)。

唐跃跃(1985-),男,山东淄博人,伊犁师范学院硕士研究生。研究方向:有限群。

O152.1 文献标识码:A 文章编号:1671-4288(2010)04-0079-02