基于位移的格子法模拟弹性波传播与应用*

熊 浩 高广运 冯世进 欧湘萍

(台州学院建筑工程学院1) 台州 318000) (同济大学地下建筑与工程系2) 上海 200092)

(同济大学岩土及地下工程教育部重点实验室3) 上海 200092) (武汉理工大学交通学院4) 武汉 430063)

0 引 言

弹性波传播的数值模拟在铁道及城市轨道交通环境振动分析和隔振设计、地震勘探等领域有广泛的应用.有限差分法、有限元法和伪谱法是三种主要的数值模拟方法.Virieux等[1]提出了基于应力-速度混合变量弹性波方程的交错网格差分法,提高了差分法的计算精度和稳定性.裴正林[2]将交错网格计算技术与高精度差分计算格式结合起来,用于三维波动模拟.Chen[3]则进一步提出了旋转交错网格计算技术,增加了差分法模拟非均匀介质中波动问题的能力.有限元法虽理论成熟,适应性强,但计算所需存储空间较大,计算效率稍差.伪谱法[4]则采用快速傅立叶变换计算空间导数,用差分法计算时间导数.通过引入映射函数虽可以使其在计算中考虑地表形状的变化,但如何合理选择映射函数有一定困难.

近年来,张剑锋[5-6]给出了基于应力-速度混合变量弹性波方程及任意四边形网格差分算子的数值方法——格子法,它融合了有限元可以适应复杂形状边界条件、有限差分法计算简便及无须计算刚度矩阵的优点,可以方便地引入任意形状自由表面边界条件.

本文基于以位移为变量弹性波方程,给出了二维格子法的计算方法,推导适合该法的人工边界条件,并通过经典Lam b问题算例验证了该方法的正确性.与传统的基于混合变量的格子法相比,该方法采用单点高斯积分法计算线积分,提高了积分的准确性;文中所给出的人工边界条件计算简便,透射外行波效果良好.应用上述数值计算方法,本文分析了在不同填充沟深度条件下的隔振效果,即地表竖向振幅衰减系数变化.

1 计算方法

1.1 基本计算公式

在笛卡尔坐标系中,不计体力,均质弹性介质中弹性波传播控制方程为

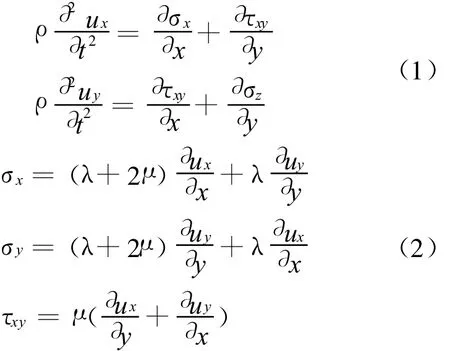
式中:ρ为弹性介质的密度,kg/m3;μ和λ为介质的Lamé系数,Pa;σx,σy,σz和 τxy为应力张量,Pa;ux和uy为位移,m.

将计算区域以三角形或四边形网格进行离散,局部网格如图1所示.图中的实线是离散时所生成网格线,实心点j,k,l,…是网格线顶点;图中的虚线是各段实线中点与网格中心点的连线,四边形网格中空心点(如1,2,3,…)是各段虚线的中点,而三角形网格中的空心点(如点7)是三角形的中心点.如果在实心点处定义位移分量ui(i=x,y),那么对于四边形网格而言,可以利用任意四边形网格差分算子[6]计算位移在域内任意点处的空间一阶导数值.

图1 局部网格示意图

对于三角形网格,以图1中三角形 fm j为例,其中心点处的位移空间一阶导数计算公式为[7]

式中:A为三角形 fm j的面积;(ui)f,(ui)m和(ui)j为三个顶点f,m,j处的位移值;bf=(yjym)/2,cf=(xj-xm)/2,(f→m→j→t),通过下标轮换可以类似地计算出 bm,cm等;(xj,yj),(xm,ym)分别为j,m点处的坐标.

从图1可见,各个实心点周围的虚线都围成一个闭合区域.假定结点 f周围虚线所围的区域为 Ω,其边界1-2-3-4-5-6-7记为 Γ.在 Ω上对式(1)积分可得

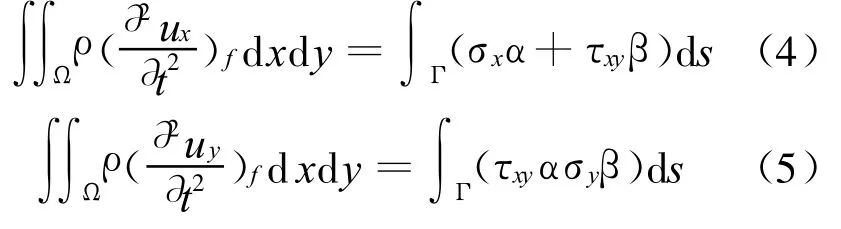
式中:α,β分别为边界 的外法线方向余弦.采用集中质量模型,式(4)～(5)中的等号左端的面积积分可简化为仅与 f点加速度有关,即分别为.式中:M f是区域 Ω的质量.对于式(3)右端的线积分,在边界Γ每一段上采用单点高斯积分公式进行数值计算.此时,每段上的积分点正是边界 Γ上的各个空心点.设式(4)和式(5)线积分值分别为(Ax)f和(Ay)f,则

对式(6)中二阶导数应用中心差分公式计算,可得

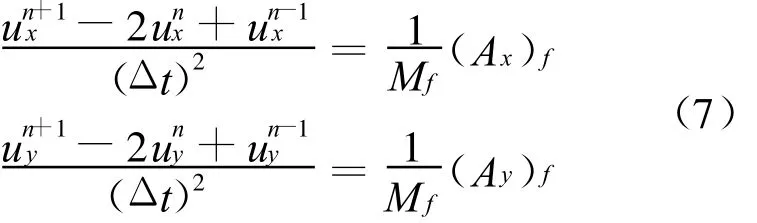
式中:上标 n为nΔt时刻,类似地n+1代表(n+1)Δt时刻,n-1为(n-1)Δt时刻;Δt为计算时间步长.根据式(7),可求得

1.2 计算步骤

对节点 f而言,应用单点高斯积分公式,在边界Γ上计算式(3)中线积分(Ax)f和(Ay)f,并把它们代入到式(7)中,计算出(n+1)Δt时刻的位移(un+1x)f,(un+1y)f.这样,就完成了 f点从nΔt时刻到(n+1)Δt时刻的位移分量递推计算.对于其他实心点,可以类似于 f点进行处理.从而整个实线网格上的全部节点在(n+1)Δt时刻位移可以完全确定.类似地,可以计算出(n+1)Δt时刻的位移场,直到设定的计算时间终点为止.

为了保证计算的稳定,时间步长Δt与空间最小网格边长h应满足稳定条件:Δt≤h/vp,式中:v p为纵波的波速.

1.3 自由表面边界条件

假定在图1中h,l,k是自由表面边界上的节点.在 l点处,在围线 l-Ma-9-3-2-8-Mb所围区域内类似于式(4)～(5)建立平衡方程

式中:M l为上述围线所围区域的质量.

式(9)中线积分分为两部分,其中Ma-9-3-2-8-Mb线段上的积分计算方法与前述式(4)～(5)中的线积分计算办法完全相同.而Mbl-Ma线段上的积分事实上就等于作用于表面边界上的已知外荷载.因此,在自由边界上边界条件可以方便地引入到计算中.

2 人工边界条件

考虑到实际上波的传播是在半无限域中进行的,而计算模型只能是有限的,因此必须在计算区域的边界上引入人工边界条件,以准确地模拟波的无限传播.本文给出一种简单实用的人工边界条件.

将式(2)代入到式(1)中,可得

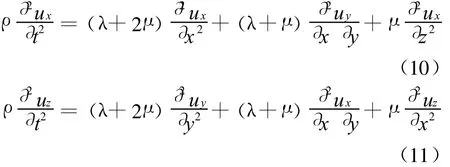
假定xoy坐标系旋转θ角得到新坐标系xoy′,其坐标轴x′与平面上某处波的传播方向相一致,忽略另一个轴方向波的传播,亦即假定∂/∂y′=0.两个坐标系之间有如下关系式

由此,可得

把式(13)代入到式(10～11)中,可得以矩阵表示的方程

对Q作特征值分解,Q=P-1ΛP,于是式(14)可以写成

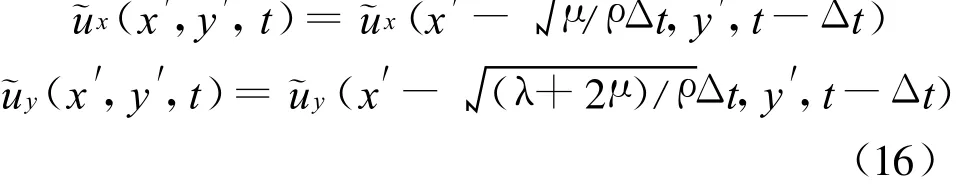
把xoy系中PU表达式代入上式中,可得

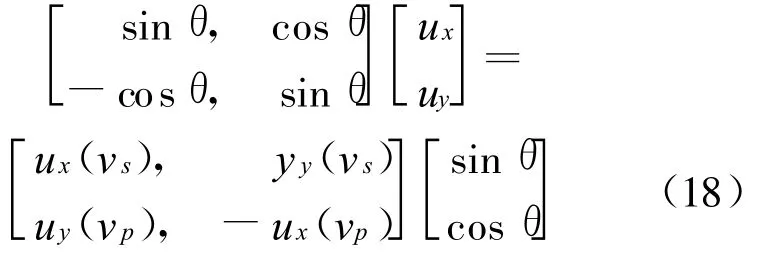
式中 :ux(vs)=ux(x-vsΔt cosθ,y+vsΔt sin θ,t-Δt),其余类似.由式(18)不难得到ux,yy的计算表达,可以发现边界节点位移由前一时刻的邻近节点的位移计算确定.在不同的边界上,应选择不同的θ,例如在边界法线与 x正方向平行的边界上,应取θ=0°计算,而在边界法线方向与y轴的负方向上一致的边界上,则应取θ=90°计算.

3 计算方法的验证

为了本文计算方法的正确性,这里计算了Lamb问题,并将计算结果与解析解[8]进行了对比.假定半无限地基密度 ρ=2 250 kg/m3,其Lamé系数 μ=1.048×103MPa,λ=1.863×103MPa;计算区域为2 000 m×1 000 m的矩阵区域,采用边长为5 m的正方形网格,时间步长取为0.002 s;振源为一垂直作用在地表中点的集中荷载,其表达式为 f(t)=exp(-200(t-0.178)2);计算采用上述人工边界条件.图2同时给出了地表上距垂直力源距离为500 m的点水平位移的解析解和本文数值计算结果,并给出了无人工边界时的数值解结果.由图可知,采用本文所述的计算方法及人工边界条件所得的数值结果与解析解答基本吻合,由此可见本文方法的正确性;对比无人工边界条件计算结果与有人工边界条件计算结果,可见本文所述的人工边界可以较好地透射出外行波,是一种有效的人工边界条件.

图2 水平位移分量的解析解与数值解的比较

4 填充沟隔振分析

振动对人们的生活与工作环境造成了不可忽视的影响,振动已被列七大公害之一.治理环境振动的有效途径之一是设置屏障隔振,填充沟就是屏障隔振措施之一.利用上述的计算方法,本文研究了采用填充沟进行隔振时,不同的填充沟深度条件下的竖向振幅衰减变化.

图3是计算模型.均匀弹性半空间地基的密度为ρs=2 000 kg/m3;剪切模量为G s=1.923×107Pa;泊松比v s=0.3.填充沟内填充物为橡胶,其密度ρ=1 200 kg/m3;剪切模量为G=9.655×105Pa;泊松比υ=0.48.振源是频率为5 H z的正弦力,表达式为 f(t)=sin(10πt).假定填充沟的宽度不变,为2m;深度h变化,分别取10,12,15,18和20m;填充沟距振源为L1=50m;在填充沟后的地表,选取与填充沟距离为L2的若干个观测点.

图3 填充沟计算示意图

Woods[9]研究屏障隔振时,提出在频域分析中,对于隔振效果可采用振幅衰减系数 AR来衡量.类似地,本文定义竖向振幅衰减系数

用于评价隔振效果.根据这一定义,如果¯AR值越小,则表明隔振的效果越好,反之则表明隔振效果不佳.

图4是计算结果.为便于分析,图中长度采用量纲一的量的长度:L*2=L2/λR,h*=h/λR,λR 是R 波波长,λR=18.188 m.由图可知,对于所设置的不同填充沟深度,都可以取得一定的隔振效果.在计算模型中,随着沟深度的逐步增加,各点隔振效果先有不同程度地降低,但当h*≈λR时,各点隔振效果却达到最佳水平.这表明,增加填充沟深度最终是有助于增加隔振效果的.对于某一填充沟深度而言,填充沟后地表各观测点的竖向振幅衰减系数均在 L*2=1.10λR～3.10λR,L*2=3.50 λR～4.75λR范围内相对偏大,而在 L*2=3.30λR和L*2=4.95λR处相对较小.这说明:一方面,填充沟的深度达一定值后其变化对于竖向振幅衰减系数¯A R影响不大;另一方面,填充沟的隔振效果是随距离L*2而不断变化的,在不同的距离处隔振效果相差较大,且存在着某个点,对应着最小竖向振幅衰减系数.所以在设计填充沟时,应注意选择填充沟的位置,确保隔振保护区域为最小竖向振幅衰减系数,以达到最佳的隔振效果.

图4 不同填充沟深度h*时竖向振幅衰减系数随距离L*2变化曲线

5 结 论

1)本文基于以位移为变量弹性波方程,给出了二维格子法的计算方法,并推导适合该法的人工边界条件.

2)经典的Lam b算例表明了本文计算方法的正确性和边界条件的适应性.该方法能很好地适应不规则的边界条件,且计算简便、准确,可用于弹性波传播及散射问题研究.

3)填充沟屏障隔振分析表明,增加填充沟深度有助于增加隔振效果,但填充沟深度并不影响最小竖向振幅衰减系数点的位置.

[1]V irieux J.P-SV w ave p ropagation in heterogeneous media:velocity-stress finite-difference method[J].Geophysics,1986,52(4):888-901.

[2]裴正林.三维各向同性介质弹性波方程交错网格高阶有限差分法模拟[J].石油物探,2005,44(4):308-316.

[3]Chen H,W ang X M,Zhao H B.A rotated staggered grid finite-difference with the absorbing boundary condition of a perfec tly matched layer[J].Chinese Science Bulletin,2006,51(19):2304-2314.

[4]Tessmer E,Kosloff D,Behle A.Elastic wave propagation simu lation in the p resence of surface topography[J].Geophysical Journal International.1992,108:621-632.

[5]Zhang JF,Liu T.P-SV-wave propagation in heterogeneousmedia:G ridmethod[J].Geophysical Journal International.1999,136,431-438.

[6]张剑锋.弹性波数值模拟的非规则网格差分法[J].地球物理学报,1998,41(增刊):357-366.

[7]Cook R D.Concepts and applications of finite element analysis[M].New York:John Wiley&Sons,1974.

[8] Lamb H.On the propagation of tremors over the surface of an elastic so lid[J].Philosophical Transactions o f the Royal Society of London,1904,203:1-44.

[9]Woods R D,Barnet N E,Sangesser R H.A new tool for soil dynamics[J].Journal of Geotechnical Engineering,1974,100(11):1231-1247.