非均布动荷载作用下沥青路面粘/线弹性有限元分析*

高梦起 何 杰 王鹏英 陈一锴

(东南大学交通学院1) 南京 210096) (河南省交通科学技术研究院有限公司2) 郑州 450006)

(郑州市公路勘察设计院3) 郑州 450006)

我国传统路面设计方法采用静力学弹性层状体系理论,不考虑车辆、路面结构和材料的动力特性.然而,在车轮与路面的相互作用中,路面结构承受的是动荷载作用.试验研究结果显示[1],轮胎作用于路面的形状更接近于矩形,作用面内的垂直力呈明显的非均匀分布特性.为探求非均布动荷载下粘/线弹性沥青路面模型之间的动态响应差别,利用ANSYS有限元软件建立半刚性基层沥青路面结构模型,考虑矩形印迹及竖向动态力的作用,分别对线弹性和粘弹性沥青路面结构模型施加非均布动荷载,进行非线性求解计算,并对两种路面模型下的力学响应进行分析和比较.

1 路面有限元瞬态动力学方程

本文依据瞬态动力学进行动态分析,瞬态动力学求解的运动方程[2]如下.

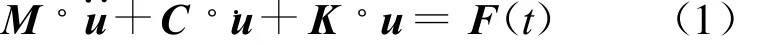
式中:M为路面系统总质量矩阵;C为路面系统阻尼矩阵;K为路面系统刚度矩阵;u为路面离散节点位移向量;F(t)为车辆荷载矩阵.

2 半刚性基层路面三维有限元分析模型

2.1 路面结构模型

在三维有限元分析中,将路面结构简化为4层:沥青面层、基层、底基层和土基,各层根据实际设计采用不同的材料属性.路面模型的参数见表1.

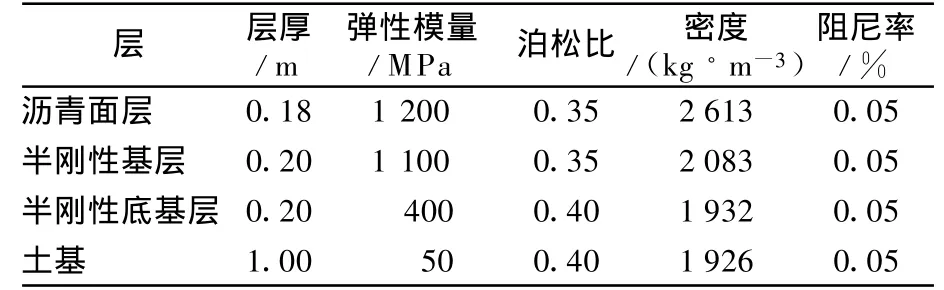
表1 路面模型参数

本文在计算中取路面模型的长、宽和高分别为6,4,1.58 m.根据ANSYS软件提供单元的材料属性,在线弹性分析中采用ANSYS中的8节点solid45单元类型;在粘弹性分析中,采用ANSYS中的8节点solid185单元类型.划分网格时,考虑到计算机效率和计算精度,在所研究路面车辆行驶区域内网格划分较密,而将其他区域网格粗化.单元数目为25 714个,有限元模型如图1所示,X正方向为行车方向.

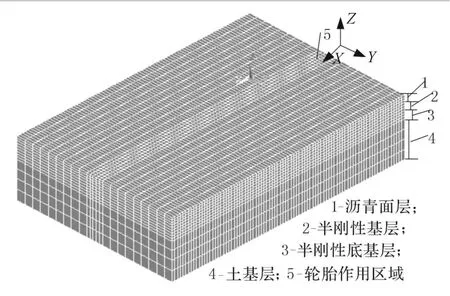
图1 路面结构有限元模型

2.2 边界条件及非均布动荷载

为了便于有限元分析,对层状的路面体系作如下基本假定[3].

(1)各层皆由均质、各向同性的线弹性/粘弹性材料组成,应力-应变呈线/粘弹性关系;(2)土基在水平方向和深度方向均为无限,其上各层厚度均为有限,水平方向仍为无限;(3)上层作用载荷,下层无限深处及水平无限远处应力和应变均为零;(4)各层之间的接触面为层间完全连续,其上位移完全连续.

车辆行使在路面的中央时,路面两端较远处基本上没有响应,如同固定约束,因此本文中路面两端的边界条件采用固定约束.

南非学者M·Beer[4]对一些型号的轮胎作用于对路面的压力分布进行量测发现,轮胎在一定负荷范围内,其中部(约占整个轮胎宽度的60%)的接地压力是基本保持不变的,而增加的荷载被作用在轮胎的两侧,如图2所示.按测量结果回归出来的接地压力分布公式为

式中:F为轮胎负载,kN,且其适用范围为20～50 kN;P为轮胎胎压,kPa.且其适用范围为420～720 kPa;P0和P1分别为轮胎荷载接地印迹内的中心区压力和边缘区压力.

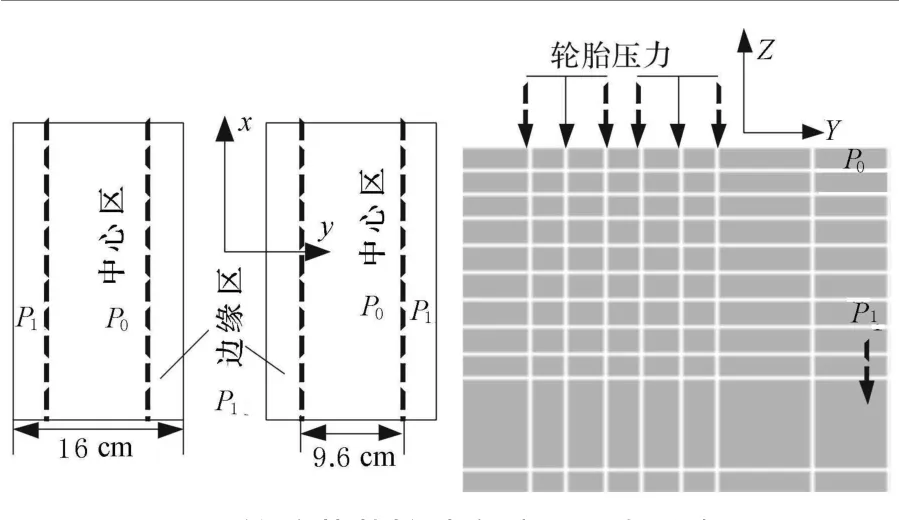
图2 轮胎荷载接地印迹及压力分布图

在有限元计算分析时采用CA 1150P1K 2LZA 80解放8 t载货车型,单轮负荷25.4 kN,轮胎接地印迹取为矩形,计算采用双轮辙作用,每个轮胎接地矩形面积为 0.21 m×0.16 m.根据80 km/h的车速计算,采用阶跃式载荷进行加载.求解时采用ANSYS软件提供的Fu ll法,并用瞬态求解器进行动力方程的求解,分析点取取动荷载第40步时(路中央)路面最大受力位置处的垂直各层关键点.

3 粘/线弹性计算结果比较及分析

限于篇幅,这里仅选用了路面结构模型各层的垂直位移、垂直应力和水平剪应力等计算结果,进行比较和分析.

3.1 路面各层动态响应的垂直位移比较

图3为路面动态响应垂直位移时间历程曲线,由图形可知线弹性和粘弹性路面各层在垂直位移上非常接近,粘弹性路面略小于线弹性路面,沥青表面层顶部(曲线1)的位移最大,达到0.093 mm,其他各层垂直位移随着路面深的增加而减小,土基层中部(曲线10)的位移为0.038 mm.

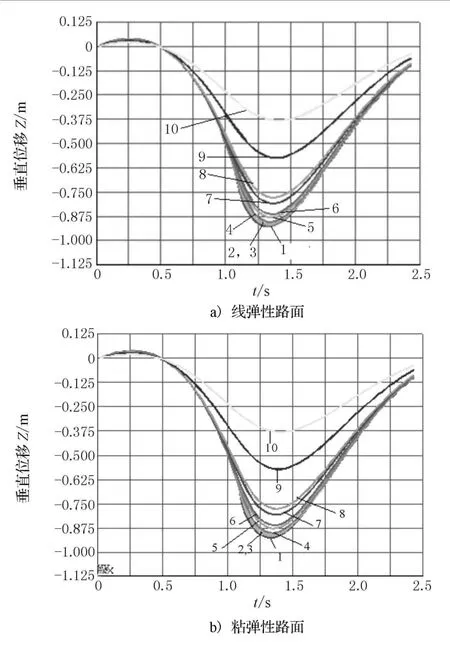
图3 路面各层垂直位移时间历程曲线

3.2 路面各层动态响应的垂直应力比较

路面各层动态响应的垂直应力时间历程曲线见图4所示,垂直应力随着深度的增加而减小.沥青层表面层(0～6 cm)范围内的压应力最大,6 cm以下压应力减小得较快,到土基层后,压应力表现为一很小的值(曲线9,10).线弹性路面沥青层垂直应力较粘弹性路面大,沥青表面层顶部约是后者的1.3倍,中面层底部和下面层底部分别约是后者的1.1倍;粘弹性路面在基层与底基层结合处(曲线5)、底基层与土基结合处(曲线6)拉应力较线弹性路面大,约是后者的1.1倍,在其他各层垂直应力则均小于线弹性路面.随着荷载的逐渐消失,弹性路面应力的消散速度明显比粘弹性路面快.

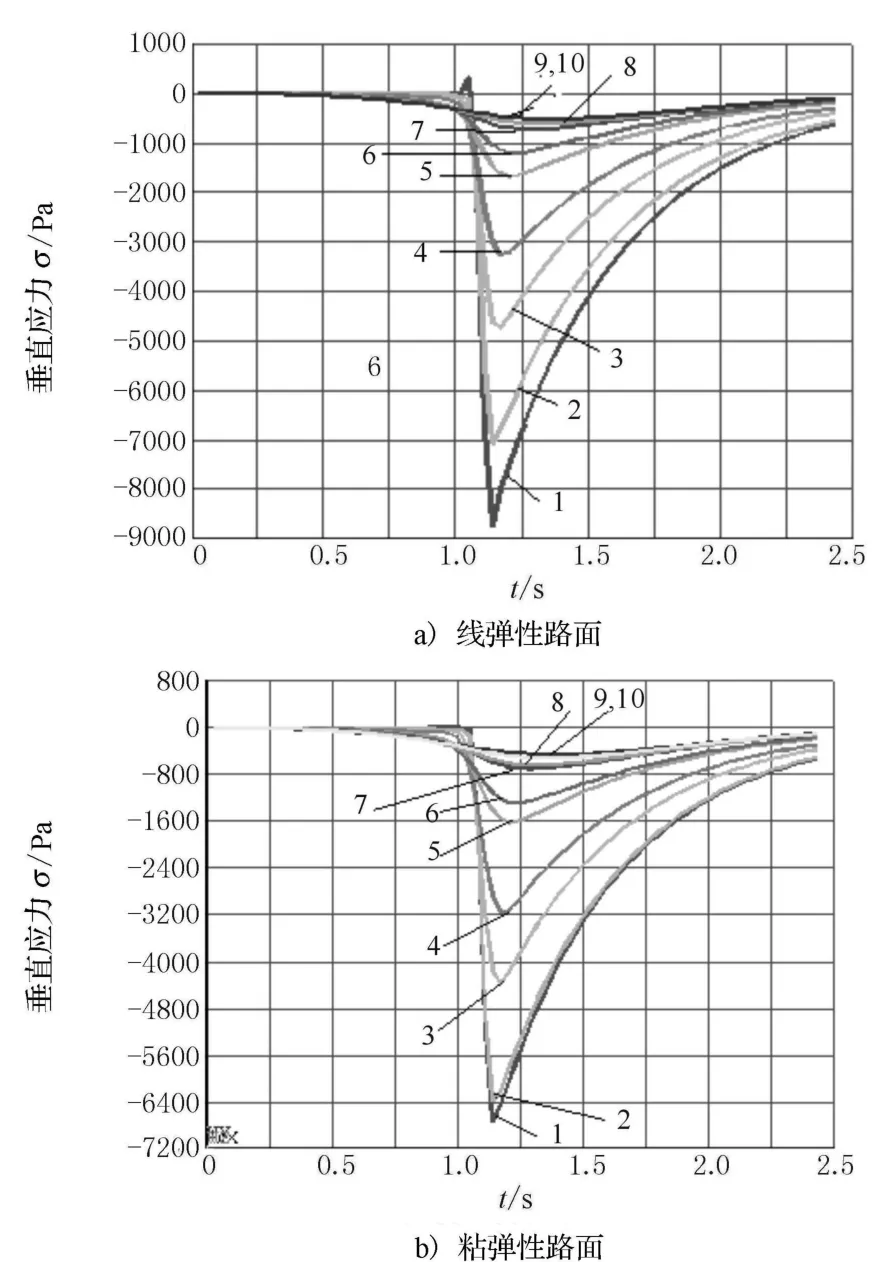
图4 路面各层垂直应力时间历程曲线

3.3 路面各层动态响应的水平剪应力比较

路面动态响应的水平剪切应力时间历程曲线见图5所示,轮载作用之前路面各层所受的水平剪切应力的作用方向与车轮行驶的方向相同,表现为正;轮载作用之后,水平剪切应力的作用方向变为与车轮行驶方向相反,表现为负.其中,在沥青层中,剪切应力随深度的变化较大,在0～6 cm时,剪切应力相对同层较小,6～15 cm之间剪切应力增长很快,在沥青底面层下部达到最大值.在沥青层上面层,粘弹性路面的水平剪应力比线弹性路面大,约是后者的1.05倍;在其他各层,粘弹性路面水平剪应力均小于线弹性路面.

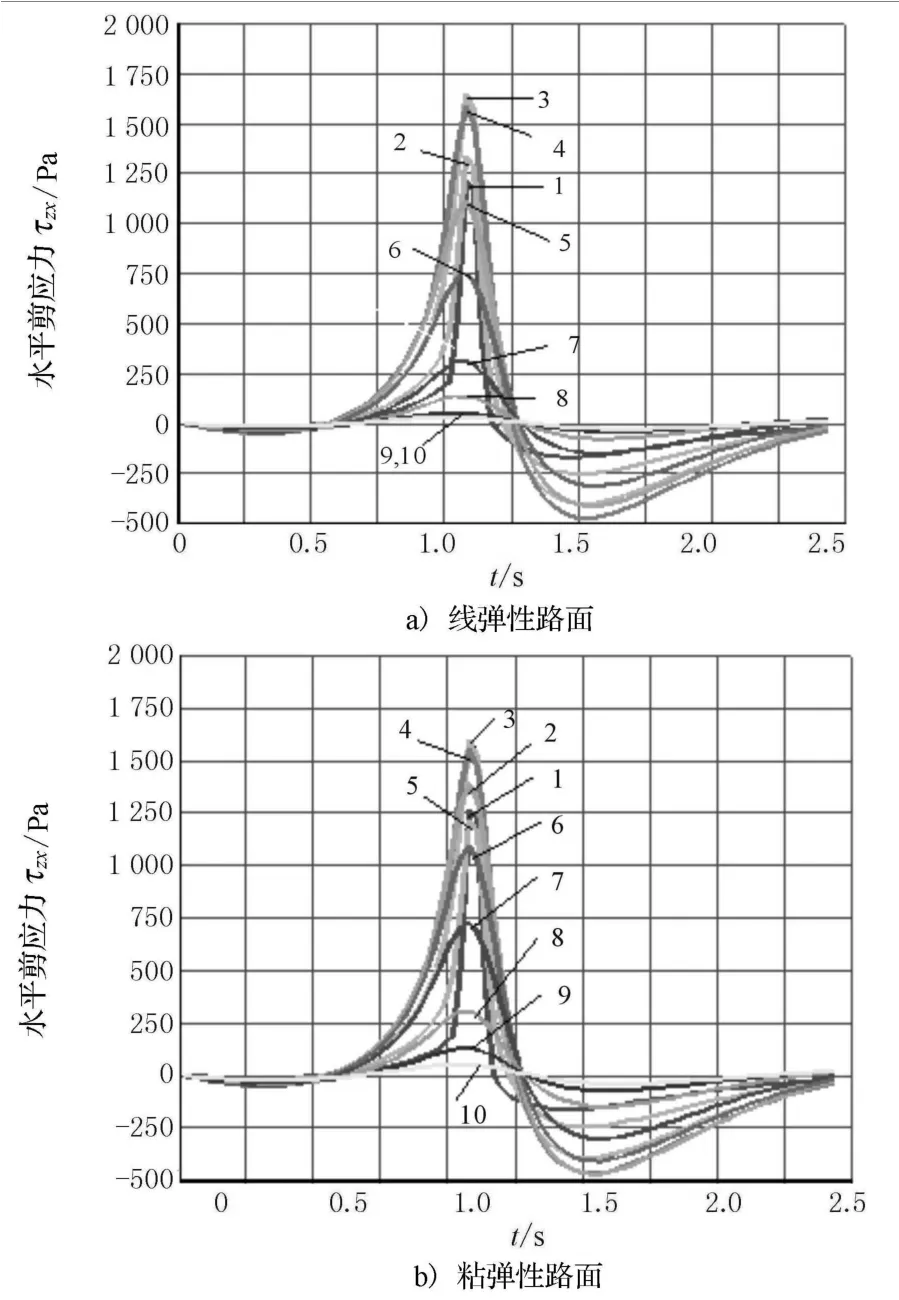
图5 路面各层水平剪应力时间历程曲线

3.4 沥青面层应力实测验证

研究证明,常温下沥青路面材料呈粘弹性质[5].根据对通车不久的上海A 5嘉金高速5标段沥青路面层压力测试值[6],试验车型轮胎压力下的应力数据并分别与两种路面模型下的计算结果对比,发现实测数值在总体上更接近粘弹性路面模型计算结果,见表2.说明,粘弹性路面模型较线弹性路面模型更接近实际,更能反映路面在动荷载下的受力状态.

表2 沥青层垂直应力实测值与仿真计算值对比表 Pa

4 结 论

1)考虑荷载的动态性和轮胎接地压力的非均布性,分别对线弹性和粘弹性三维有限元半刚性沥青路面结构模型施加了相同的动荷载,并比较分析了这两种路面模型的力学响应.

2)两种路面结构模型具有一致的力学响应规律,时间历程曲线形式基本一致,但线弹性路面模型在路面主要部位的应力均大于粘弹性路面模型,且随着荷载的消失,路面各层应力的变化速度明显快于粘弹性路面模型.

3)线弹性路面模型在力学响应分析中会使计算结果偏大,并存在一定的失真,而粘弹性路面模型相对更符合实际.

[1]酒井秀男,管建民.关于橡胶及轮胎接触压力分布的测定和图像处理研究[J].橡胶业,1995,42(11):682-692.

[2]尚晓江.结构有限元高级分析方法与范例应用[M].北京:中国水利水电出版社,2005.

[3] 朱照宏,王秉刚,郭大智.路面力学计算[M].北京:人民交通出版社,1985.

[4] de Beer M,Fisher C,Jooste F.Determ ination of pneumatic tire.Pavement interface contact stresses under moving loads and some effects on pavements w ith thin asphalt surfacing layers[C].The 8th international Con ference on Asphalt Pavement.W ashington:1997:179-226.

[5]张久鹏,黄晓明,赵永利.沥青路面车辙处沥青迁移规律及其粘弹性力学机理[J].武汉理工大学学报:交通科学与工程版,2008,32(4):596-599.

[6]上海市公路工程质检中心.上海A 5嘉金高速公路5标段沥青层压力检测报告[R].上海:上海市公路工程质检中心,2007.