基于ANSYS的车辆液力缓速器叶片强度分析及模态分析*

过学迅 梁荣亮 陈 见

(武汉理工大学汽车工程学院1) 武汉 430070) (中国汽车技术研究中心2) 天津 300162)

随着车辆日益向高速重载的方向发展,液力缓速器作为一种安全可靠的高速辅助制动装置而被广泛的普及应用[1-3],液力缓速器结构如图1所示.当液力缓速器高速制动时,转子(泵轮)叶片随传动主轴高速旋转并带动工作腔内的工作油液对固定于箱体的定子(涡轮)叶片产生很大的表面冲击,如果工作轮载荷超出所选用材料的强度极限,液力缓速器高速制动时容易导致叶片断裂,存在安全隐患,所以对叶片进行强度分析是液力缓速器选材制造的前提[4];同时,油液在工作腔流道中的流动是粘性、不可压缩的三维不稳定的复杂流动[5],流动规律难以准确测量,工作状态下,不仅其内部能量转换和工作油的流动状态极其复杂,而且还承受来自于路面激励和发动机以及传动系统的高频振动,所以有必要对液力缓速器进行模态分析,求得各阶振型的固有频率,使液力缓速器工作时避免共振.

1 ANSYS有限元模型的建立

图1 液力缓速器结构简图

利用流体计算仿真软件Fluent获得液力缓速器在最高转速3 000 r/min工况下的转子叶片和定子叶片压力面受到的工作液液体总压的分布情况[6],并将叶片表面各个离散点的液体总压导出到EXCEL中,得到叶片表面液体总压的分布规律.

转子叶片压力面受到的最大液压为17.6 MPa,最小液压为-5.12 MPa,而定子叶片压力面受到的最大液压为 11.2 MPa,最小液压为-4.95 MPa,故只需对转子叶片进行有限元分析即可.在有限元分析计算过程中,为了保证较高的计算精度,通常需要对模型进行网格的局部细化,但会占用过多的计算空间,使得计算速度大大降低.由于液力缓速器所有叶片沿中心轴线呈现圆周阵列分布,为了在有限的计算资源的前提下获得较高的计算精度,同时为了更加清晰精确的显示叶片的应力及应变,可以提取液力缓速器的一个单独叶片进行分析并借助于UG与ANSYS的数据接口,将叶片模型导入ANSYS生成有限元模型.但是在进行上述操作之前有必要对模型做局部的简化修正,防止因局部造型的复杂而导致网格划分的失败.

2 有限元模型的强度分析

叶片有限元模型几何外形复杂,并且叶片的内表面是工作液液体总压的主要承载面,为得到高精度的计算结果,采用solid95实体单元重点对叶片承载面进行局部网格细化,共生成44 139个节点和26 421个单元.在所建立有限元模型的基础上,忽略粘性剪切力对叶片强度的影响,在有限元模型的周期切割面上施加周期对称约束,并在轮毂处施加全方位的零位移约束.由液力缓速器的工作原理可知,液压油在封闭的工作腔内高速旋转,在很高的离心力作用下对叶片的工作面产生压力载荷.离心力的计算公式如下.

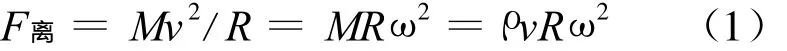
式中:ρ为工作液液体密度;v为填充到工作腔内的液体体积;R为工作轮的旋转半径;ω为工作轮的旋转角速度.

所以在某一恒定稳态转速下工作液的密度和体积不会变化,可以近似认为离心力与旋转半径成线性关系.所以,液体总压在各个叶片压力面上的分布规律为沿旋转半径的递增而线性递增.根据空间解析几何理论,有限元模型沿径向方向的递增斜率为0.45MPa.有限元模型位移约束及载荷约束如图2所示.该液力缓速器选用ZL104铝合金材料,弹性模量为80GPa,泊松比为0.33,密度为2 800 kg/m3.

在ANSYS通用后处理中,获得有限元模型的结构变形情况和等效应力分布情况,如图3、图4所示.最大变形量为0.365 501 mm,发生在叶片中心偏向外环处,最大等效应力为378MPa,出现在靠近流道外环的叶片根部.为便于详细观察转子叶片表面沿旋转半径方向的变形量及等效应力的变化,在叶片工作面外端选取一轨迹线如图5所示,轨迹线上各个节点的变形量及等效应力变化如图6、图7所示,沿轨迹线方向上的叶片最大变形量为靠近叶片外环处,最大等效应力沿轨迹线方向逐渐递增,最高等效应力部位位于叶片和外环壳体的根部,有限元模型强度分析结果与真实情况基本吻合.

图2 施加在有限元模型上的约束

图3 有限元模型的结构变形

图4 有限元模型的等效应力分布

图5 转子叶片上选取的轨迹线

图6 轨迹线节点上的变形量

图7 轨迹线节点上的等效应力

3 有限元模型的模态分析

对有限元模型按照强度分析的过程和步骤进行单元材料属性的设置、网格的划分、位移约束的施加,在0～100 H z的频率范围内对有限元模型进行6阶模态分析.

1阶振型为外环及叶片沿缓速器基准轴方向前后俯仰振动,振动固有频率为1.536 H z,最大变形量为0.957×10-4m,如图8所示;2阶振型为外环及叶片沿叶片向两侧摆动,振动固有频率为3.289 H z,最大变形量为0.319×10-3m;3阶振型为外环及叶片沿外环腰鼓内外摆振,振动固有频率为5.039 H z,最大变形量为0.213×10-3m;4阶振型为外环及叶片沿叶片内外两侧摆振,振动固有频率为5.592 Hz,最大变形量为0.284×10-3m;5阶振型同三阶振型相似沿外环腰鼓内外摆振,振动固有频率为6.593 Hz,最大变形量为0.366×10-3m;6阶振型沿叶片上下摆振,振动固有频率为8.434 Hz,最大变形量为0.334×10-3m,如图9所示.液力缓速器作为高速制动辅助装置,其工作转速范围为600～3 000 r/min,对应的固有振动频率范围为10～50Hz,高于模态分析各阶振型的固有频率,从而在工作状态下能够避免共振的发生.

图8 有限元模型1阶振型矢量位移

图9 有限元模型6阶振型矢量位移

4 结 论

1)该液力缓速器选用ZL104铝合金材料的强度极限为490MPa,屈服极限为350 MPa,由有限元模型的强度分析可知,转子叶片在外环根部的等效应力已经超过该选用材料的屈服极限,所以在该部位最容易产生应力集中,存在安全隐患,长时间持续工作有可能导致叶片根部发生断裂,应当采用强度更高的铸钢材料.根据GB/T14408-1993,推荐采用ZGD410-620铸钢(弹性模量为175GPa,泊松比为0.30,密度为7 850 kg/m3,强度极限为620MPa,屈服极限为410 MPa,强度安全系数n b=4.0),可得铸钢压力容器承压部件的强度许用应力为155 MPa,远高于转子叶片压力面受到的最大液压(17.6 MPa),保证缓速器在最高转速下的稳定可靠的力学性能.

2)对有限元模型施加载荷时,近似模拟叶片上的液压载荷为沿旋转半径方向的线性分布,而真实情况下,考虑到油液的粘性、油液与壁面的边界层的处理、工作腔内空气气流的影响以及油液在叶片非压力面形成的背压等因素的影响[6],液体总压在叶片压力面上的分布是无规律可循的,所以有限元模型的仿真载荷与真实情况还存在一定的误差,需要更加精确的载荷定位.

3)在进行液力缓速器结构设计时,建议在工作叶轮与外环壳体交接处采用圆角过渡,提高叶片根部的抗疲劳强度,衰减应力集中.

[1]时 军,过学迅.车用液力减速制动器的现状与发展趋势[J].车辆与传动技术,2001(4):1-3.

[2] 刘应诚,邵万珍.车用液力减速(制动)器[J].现代零部件,2005(2-3):1-2.

[3]杨凯华,郑慕桥,阎清东,等.车辆传动中液力缓速器的技术发展[J].工程机械,2001,32(6):1-3.

[4]王 峰,阎清东,乔建刚.液力缓速器制动性能的计算方法[J].起重与运输机械,2006(5):2-4.

[5]马文星.液力传动理论与设计[M].北京:化学工业出版社,2004.

[6]李吉元.牵引-制动型液力变矩器流场分析及一体化设计研究[D].北京:北京理工大学机械与车辆工程学院,2005.