船舶阻力计算BP神经网络的研究*

陈爱国 叶家玮 苏 曙

(广州航海高等专科学校轮机系1) 广州 510725) (华南理工大学土木与交通学院2) 广州 510640)

船舶 的计算,由于问题的复杂性,目前还没有成熟 理论的公式,一般在船舶线型确定时可通过 实验来确定,但在设计的初期或并不准备作 实验时,只能进行阻力近似计算.阻力近似计 常用方法一般都是通过查阅大量图表的方式来进行计算,工作量大且精度低.

Lippm ann[1],Funahashi[2],Hornik[3]等人对神经网络的研究已表明:3层以上的前向神经网络能以任意精度逼近任何非线性性函数,因此采用多层前向神经网络来逼近以船型参数和速度流体参数为自变量的船舶阻力函数在理论上是可行的.为此本文采用系列60船模实验数据作为样本,由于作为前向神经网络核心的误差反传BP网络在函数逼近上具有优越的性能,本文力图通过实验建立出性能卓越的3层BP神经网络船舶阻力计算系统.

1 数据样本及处理

在系列60的计算中,平板摩擦阻力系数C f采用桑海公式计算,粗糙度补贴系数取0.4×10-3,其剩余阻力由船模试验确定,剩余阻力的输入数据包括3个船型参数和1个速度参数[4-5].船型参数为:方形系数C b,船长型宽比L/B,型宽吃水比B/H.输入的速度参数有2种,分别对应不同的输出参数:速长比对应的输出为每吨排水量的剩余阻力系数C R;弗氏速率系数对应的输出为弗氏阻力系数,由于后者在船舶初步设计时对船型的比较非常有用,其应用更受推荐,因此本文输入的速度参数采用弗氏速率系数对应地输出采用弗氏阻力系数.

系列60共用45个船模,共有数据838组.为检验网络的泛化能力,随机选取全部数据组中的629组作为训练数据,另209组作为检验数据.采用训练与检验神经网络时输出与目标的相关系数、回归直线、最大相对误差、平均相对误差中的差值来衡量网络的性能.

2 三层神经网络结构设计

由上面的分析可知该BP神经网络的输入层为4个神经元,输出层为1个神经元,设隐层神经元数为R,则其结构如图1所示.

为选取合适的隐层神经元数R,传递函数g1(·),g2(·),性能函数E(·)和训练函数,分别对之进行试验.

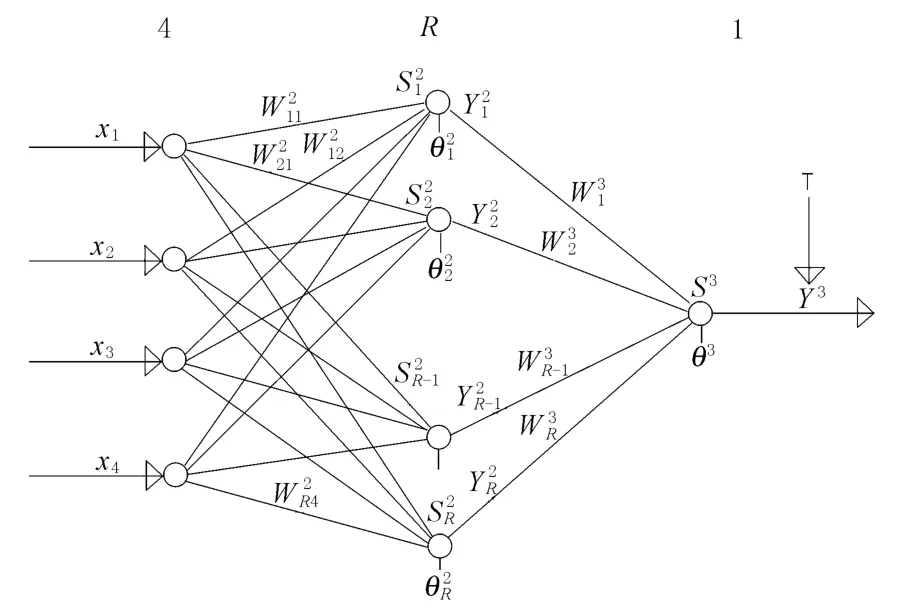
图1 船舶阻力计算3层BP神经网络结构图

2.1 训练函数和性能函数的确定

为确定该神经网络的训练函数,经初步试验决定采用15个神经元的隐层,隐层传递函数g1(·)采用 tansig,输出层传递函数g2(·)采用purelin,最大训练次数采用1 000,由于数据量较大,采用批处量训练方式,用网络输出数据与目标的相关系数(在多次训练采用较好的相关性数据)来衡量训练结果,从实验结果看,普通训练函数traingd和 traingdm收敛性差,而且增加最大训练次数,也不能提高相关系数;快速训练函数中,有弹回的BP算法trainrp比自适应修改学习率算法traingda和traingdx要好;其他的算法都可达到较高的计算精度,尤其是 traincgb,trainlm,trainbr.最好的是 trainbr,其训练的相关系数和检验的相关系数不但最大,而且两者相差最小,这是由于应用其他训练函数时,网络的性能函数E(·)是采用m se,如式(1),其中 N训练样本数,而trainbr作为规则化的调整方法是采用m sereg作为性能函数,如式(2)和式(3)所示,其范化能力更好.因此本试验的神经网络选用trainbr规则化的训练方法,对应地采用m sereg作为性能函数.

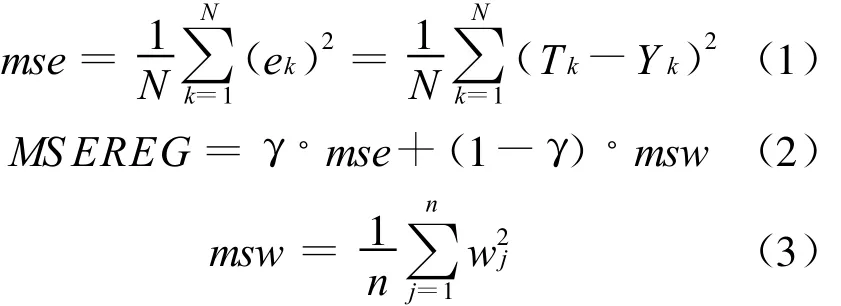
2.2 传递函数的确定

为确定该神经网络隐层和输出层的传递函数,仍采用15个神经元的隐层,最大训练次数采用1 000,采用trainbr训练函数,用网络输出数据与目标的相关系数(在多次训练中采用较好的相关性数据)来衡量训练结果.对BP网络应使用可微的函数作传递函数,对本项目不适合使用satlin,satlins,tribas,hard lim,hard lims等带水平线的非光顺函数[6],因此本实验对常用的 tansig,purelin,logsig进行组合实验,并对采用 radbas进行了2组实验,实验结果如表1.

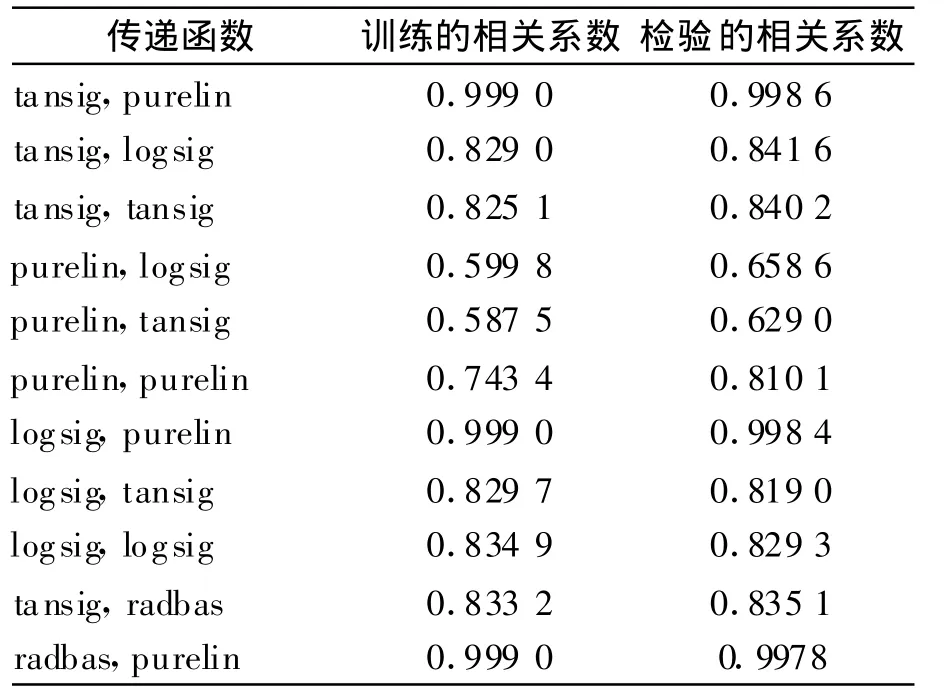
表1 传递函数实验结果

从实验结果可以分析得出,输出层采用logsig或tansig相关系数不高;隐层的传递函数采用purelin不合适,网络输出数据与目标的相关系数最小,对于使用purelin,purelin传递函数,由于是纯线性变换对非线性系统逼近能力差;而据实验结果,隐层传递函数采用tansig或logsig,输出层传递函数采用purelin可以很好地达到函数逼近,而且输出数据与目标数据的回归曲线与理想回归曲线几乎重合,对radbas的实验表明,对本项目,该函数同样不适于作输出层传递函数,当进行 radbas,purelin组合时也可达到较好的结果,但检验结果相关性比前两者稍差,从进一步的实验结果看,采用 tansig、purelin作传递函数比采用logsig,purelin要稍好一些.

2.3 隐层神经元数试验

由上面试验结果,对该神经网络隐层神经元数进行实验,隐层传递函数采用tansig,输出层传递函数采用purelin,最大训练次数采用1 000,采用trainbr训练函数,用网络输出数据与目标的相关系数和最大相对误差来衡量训练结果,编制程序,得到相关系数、最大相对误差、平均相对误差随神经元数的变化曲线如图2所示.

由图2可知,随神经元数的增加,相关系数越来越大、最大相对误和平均相对误差越来越小,但当神经元数达到15以后,变化很慢了.

2.4 采用预先数据处理训练网络

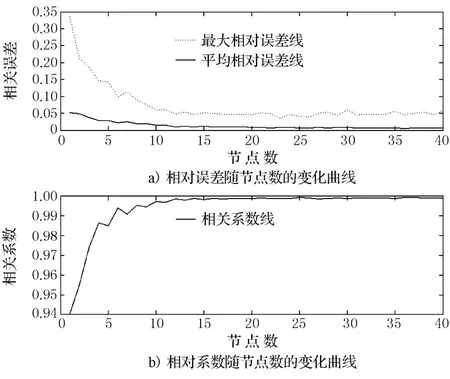
图2 相关系数最大相对误差和平均相对误差随隐层神经元数变化曲线

从上述实验可知,增加隐层神经元数可提高神经网络的性能,但由于检验数据与训练数据一样都来源于原始实验数据,对B/H仅有2.5,3.0,3.5 3个数值,对C b,L/B也只有有限的几个取值,当隐层神经元数过多时,将导致对某一参数在有限的几个取值附近具有高的精度,但在其他值则有很大的波动,这与实际情形不符.如针对23隐层神经元的神经网络,对C b=0.65,船长型宽比L/B=7.25,弗氏速率系数○k=1.4,弗氏阻力系数○C对B/H的变化曲线如图3所示,显然,此时曲线失真.同样地对15隐层神经元的神经网络绘制的曲线如图4所示,则其插值曲线是较平顺的.

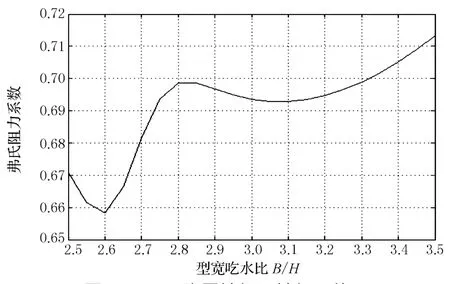
图3 用23隐层神经元神经网络绘制的○k对B/H的变化曲线

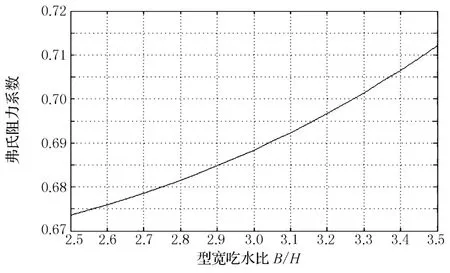
图4 用15隐层神经元神经网络绘制的○k对B/H的变化曲线

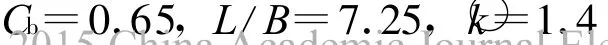
因此,为了提高网络的逼近能力和降低相对误差,对输入样本采用预先数据处理的方式,将输入向量和目标向量的值量化到[-1,+1]内,进一步训练结果如表2所列.

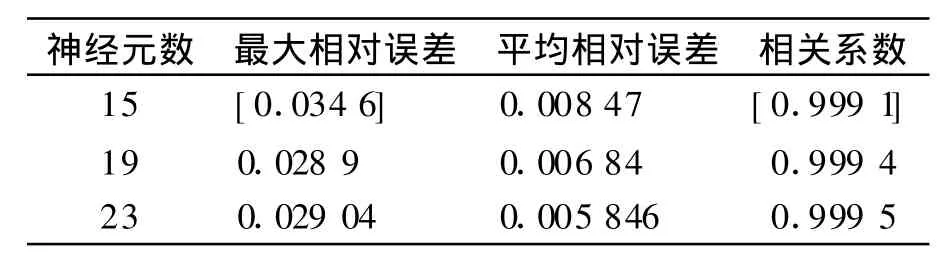
表2 预先数据处理训练结果

2.5 船舶阻力最佳BP神经网络的确定

分别应用预先数据处理训练所得的神经网络,进行绘图,根据插值曲线绘图对比,选用19神经元的最大相对误差0.028 9的神经网络,其回归曲线如图5所示,可见回归直线与理想回归直线几乎重合,而通过对最大的相对误差的样本分析发现,相对误差大的都是○k取值最大或最小的样本,这与系列60图谱是一致的,因此在实际应用范围内是有更高计算精度的,可以满足船舶设计的需要.

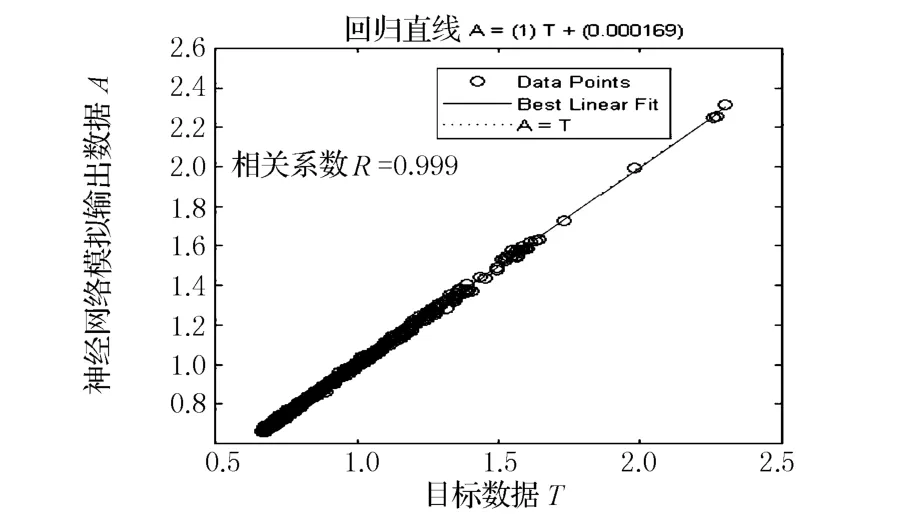
图5 隐层19神经元最佳网络回归曲线

由于,训练和检验样本都是用的原始实验数据,对B/H仅有2.5,3.0,3.5 3个数值,为验证该神经网络的泛化能力,对相同的Cb,L/B和○k,在B/H为2.5,3.0,3.5的数值之间进行线性插值,添加了B/H为2.66,2.84,3.16,3.34四组数值,插值后数据样本由838组扩充到1 869组,对该神经网络进行模拟,得到最大相对误差为0.031 63,平均相对误差为:0.007 246,输出和目标的回归直线为A=(1.000 3)T+(-0.001 513 4),可见其泛化能力是很好的.

3 船舶阻力BP神经网络的应用

3.1 计算船舶阻力的应用

该船舶阻力神经网络可以方便快速地计算弗氏阻力系数,如任意输入方形系数Cb=0.70,船长型宽比L/B=7.8,型宽吃水比B/H=3.0,弗氏速率系数=1.4,对网络进行模拟得到对应的输出弗氏阻力系数=0.696 1.经在图谱上查阅,其值接近0.7,与其结果一致.但显然对于图谱不能直接查找的数值,应用该船舶阻力神经网络更方便.

3.2 船船阻力性能研究及船型优化的应用

显然通过该神经网络能很方便地作出各种阻力变化曲线,可用于分析阻力随船型参数的变化情况.例如,在系列60船模实验中,由于对相同的一组Cb,B/H船长型宽比L/B只有3个变化的数值,弗氏阻力系数与L/B的变化关系不能很清楚地表达出来,但通过该19隐层神经元的船舶阻力神经网络,则可以方便地绘制其变化曲线,如B/H=2.5,=1.7,在不同 C b时,弗氏阻力系数船长型宽比L/B的变化曲线如图6所示,从该图可以清楚地分析出系列60船舶最低剩余阻力时的最佳L/B,及该最佳L/B随C b的增大而变小的情况.用该神经网络绘制的其他性能曲线如图7所示,显然该神经网络拓展了系列60的应用范围,并可应用于一定约束条件下的船型优化.

3.3 在船机桨匹配优化设计上的应用

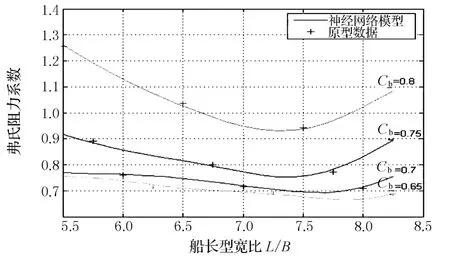
图6 隐层19神经元网络与L/B的变化曲线

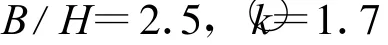
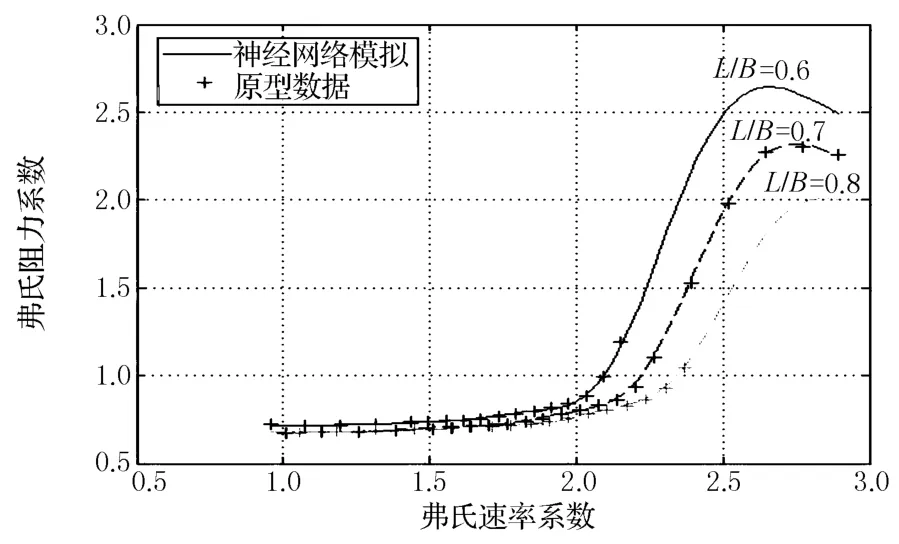
图7 隐层19神经元网络绘制的对○k和L/B的变化曲线

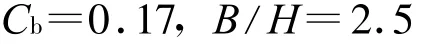
船机桨匹配优化设计时,不论是在初步匹配设计中,还是最终匹配设计中,都要计算船舶阻力,作出船舶有效功率随航速的变化曲线,该船舶阻力神经网络系统的研制为船机桨匹配优化设计的计算机化、智能化提供了重要的支撑.

4 结 论

1)利用船模原始实验数据通过预先数据处理的方式,采用tansig和purelin传递函数,以及trainbr训练函数和合适的隐层神经元数,可以训练出高精度的船舶阻力计算BP神经网络系统.

2)该神经网络系统在船舶阻力计算研究、船型优化和船机桨优化匹配设计上比传统方法具有无可比拟的优势.

3)基于神经网络能以任意精度逼近任何非线性函数的能力,抽象出更有代表性的船型参数、选用合适的速度参数,利用不同的船模系列数据,甚至是高速舰船的阻力数据,设计出具有广泛适应性的船舶阻力计算神经网络系统也将是现实可行的.

[1] Lippmamm R P.Introduction of Computing with Neural Nets[J].IEEE ASSP M agazine,1987,4:4-22.

[2]Funahashi K I.On the approximate realization o f continuous mappings by neura l netw orks[J].Neural Networks,1989,2(3):183-192.

[3]林 盾,陈 俐.BP神经网络在模拟非线性系统输出中的应用[J].武汉理工大学学报:交通科学与工程版,2003,27(5):120-123.

[4]Chen Aiguo,Ye Jiaw e.Research on the genetic neural netw ork for the computation of ship resistance[C].2009 International Conference on Computation Intelligence and Natural Computing.Wuhan,China,2009.

[5]Chen Aiguo,Ye Jiawe.Research on four layer back propagation neural netw ork for the computation of ship resistance[C].2009 IEEE International Con ference on M echatronics and Automation.Changchun,China,2009.

[6]Zhang Ling,Zhang Xianda.M IMO channel estimation and equalization using three-layer neural networks w ith feedback[J].Tsinghua Science And Technology.2007,12(6):16-19.