如何用SAS软件正确分析生物医学科研资料Ⅺ.用SAS软件实现正交设计定量资料的统计分析

柳伟伟，胡良平，陶丽新，毛玮

1 正交设计的概念及应用场合

通常情况下，可认为正交设计所确定的因素间的水平组合是析因设计所确定的因素间的水平组合的一部分。正交设计就是用一系列规格化的正交表来安排各实验因素及其水平组合的过程。与析因设计相比，正交设计是以不考察或少考察因素间高阶交互作用项为代价换取很少实验次数，从而达到安排多个实验因素且取得较可靠实验结果的目的。

在可以应用析因设计的实验研究中，若所需要的实验次数太多，并且高阶交互作用可以忽略不计时，为了减少实验次数，可以考虑选用正交设计。

2 正交表及其分类

正交表是正交设计的基本工具，它是根据均衡分散、整齐可比的思想经过严格的数学推导而编制出来的。正交表中的每一行代表各实验因素的一种水平组合，称为一个实验点；正交表的每一列代表一种实验效应，它可能代表某实验因素、交互作用或实验误差的效应[1]。每张正交表都有一个表头符号 Ln（Km），其中 L 代表正交表；n 代表正交表的行数，也就是实验条件（或实验点）数；m 代表正交表的列数，也就是正交表最多能安排的因素个数；K 代表正交表每一列中不同数字代码的个数，也就是各因素的水平数。

正交表中总的自由度等于实验次数减 1，如果每种实验条件下只做一次独立实验，总的自由度就等于正交表的行数减 1；某一列的自由度等于该列的水平数减 1[2]。

一般来说，每张正交表都有一张与其对应的交互作用表，交互作用表用来说明任意两列的交互作用列在正交表中所处的位置。

正交表可以分为同水平的正交表与混合水平的正交表两大类。同水平正交表是指各因素的水平数相同，包括二水平正交表，例如 L4（23）、L8（27）、L16（215）；三水平正交表，例如 L9（34）、L27（313）；四水平正交表等等。混合水平正交表是指各因素的水平数不全相同，例如 L8（41×24）、L9（21×32）等等。实际应用时需要注意的是，有一类正交表没有交互作用列，因此无法考察交互作用，例如 L12（211）、L18（37），它们属于非标准的正交表。

3 正交设计的特点与实施步骤

正交设计有三个突出的特点，首先，由正交表挑出来的实验点在空间上具有均匀分散性，也就是实验点在实验空间分布得很均匀，无论从哪个角度看，都是有代表性的点被挑选出来了；其次，由正交表挑出来的实验点在统计分析时具有整齐可比性；第三，某些好的未包括在正交表中的实验点，可以通过统计分析将其发现[1]。

在确定了实验因素及其水平数之后，正交设计的实施可以分以下四个步骤来完成：第一步，根据因素数及各因素的水平数选择合适的正交表，在能够安排下所有实验因素的基础上，应该选择最小号的正交表，使得需要进行的实验次数较少。第二步，在选定的正交表的表头上安排实验因素及其交互作用，这一步称为表头设计，是所有步骤当中最关键的一步。如果因素间的交互作用可以忽略不计，各因素可以任意安排到各列中去。如果某些因素间存在交互作用，就需要根据交互作用表进行表头设计。表头设计的一个重要原则是避免混杂，混杂是指在正交表的同一列上安排了两个或两个以上的因素或交互作用[3]。当每种实验条件下只做一次实验时，如果要进行方差分析，就需要在正交表中安排至少一个空白列。在一些统计书上有现成的表头设计表，可以根据这些表直接安排实验。第三步，根据设计好的表头，将标有单个实验因素的那些列连同其下的“水平代码”一起摘录出来。第四步，结合实验因素各水平的具体内容，将摘录出来的各列的“水平代码”转换成“真实代码”（即实验因素的真实水平），并按正交表各行所决定的实验条件进行具体实验。

正交设计的实施过程，以及正交表与交互作用表将通过以下的实例进一步加以说明。

4 正交设计中一个值得注意的问题

人们常以为进行正交设计就不必要进行重复实验了，即使正交表中未留下一个空白列时也是如此。这是过于迷信正交设计作用的表现。其实，通常（特指为节省样本量时）正交设计就是析因设计的部分实施，换句话说，就是仅使用实验因素全部水平组合当中的一部分，有时是很少的一部分，本质上属于“对照不全”的实验，正是由于正交设计方案挑选出来的那些实验点具有“均匀分散、整齐可比”的特点，才使其具有较好的代表性，但并不意味着在结论的可靠性上它比全面实验的析因设计还要好。析因设计中明确要求各实验条件下至少要做 2 次独立重复实验，有两个目的：第一，为了能够比较准确地估计单个实验因素的主效应和因素之间的各级交互作用的效应大小；第二，能够比较真实地显露各实验条件下的实验误差的大小，提高结论的可信度。而正交设计实际上就是以牺牲第一点中的部分利益（即不估计高阶交互作用，甚至部分低阶交互作用也不能估计）为代价，换取较少的实验次数，但它并没有能力和资格承诺各实验条件下仅做一次实验，结果就一定是稳定的！也就是说，若在一个具体实验中，仅当在特定实验条件下所得到的实验结果的波动是非常微小的（在专业上允许的范围内，相当于确定性实验结果，如在一个标准大气压下，水加热到摄氏一百度时必然沸腾），才可不做重复实验，否则必须做重复实验。至于要做多少次重复实验，取决于具体实验的误差大小和研究者对结果精确度的要求，最好根据一些基本数据和先验知识，估计出重复实验次数。

5 正交设计定量资料方差分析的SAS 实现

例1 在乙酰苯胺磺化工艺的研究中，有 4个实验因素：反应温度 A、反应时间 B、磺酸浓度 C、操作方法 D，各取两水平。实验的结果为产物的收率（%），希望弄清各因素在怎样的搭配条件下收率最高。已知反应温度与反应时间之间的交互作用不可忽视，各实验条件下不必进行重复实验，希望总实验次数尽可能少一些。4个实验因素的水平分别如下：

因素名称（单位） 1 水平 2 水平反应温度（℃） 50 70反应时间（h） 1 2磺酸浓度（%） 17 27操作方法 搅拌 不搅拌

正交设计的实施：本例如果选择析因设计，不同的实验条件数为24=16 种，各实验条件下至少要做 2 次独立重复实验，总实验次数至少为32 次，实验次数相对较多，与要求不符。由于只需要考虑两个实验因素之间的一阶交互作用，高阶交互作用可以忽略，故选择正交设计比较合适。

研究中的4个实验因素都是两水平，应该选择二水平正交表。由于只需要考虑两个实验因素之间的一阶交互作用，连同 4个两水平因素，共需要安排 5 项，每项的自由度都是 1，将占用 5个自由度。在二水平正交表中，每列的自由度为1，故需要 5 列来安排实验因素及其交互作用。如果选择 L4（23）正交表不妥，因为该正交表只有 3 列，自由度为3，用来安排该实验是不够的；若选择 L16（215）正交表也不妥，因为该正交表有 15 列，自由度为15，远远大于所需要的5 列，意味着实验次数将较多；若选择 L8（27）正交表，是非常合适的，因为该正交表有 7 列，自由度为7，比所需要的5 列多出两列，正交表中将有两个空列，可用于估计实验误差，此时，只需要做8次实验，就可以满足研究者的要求。L8（27）正交表是符合要求的最小号的正交表，具体见表1，其交互作用表见表2。

表1 L8（27）正交表

表2 L8（27）正交表的交互作用表

L8（27）正交表有 8 行 7 列，用该表来安排实验，要在8 种实验条件下总共至少做 8 次实验，最多可以安排的因素个数为7，每个因素都有两个水平，分别用 1、2 来表示。

在表 2 中，第 1个列号是由上到下编号的，代表着 7行；第 2个列号是从左至右编号的，代表 7 列。无论是 7行还是 7 列指的都是 L8（27）正交表中的“7 列”，也就是说，把 L8（27）表中的7个列号同时放在横向与纵向两个方向上。如果要查任意两列的交互作用列，只需要找到这两列列号的交叉位置的数字就可以了。例如，查第 6 列和第 7 列的交互作用列，可以横向看第 6 行、纵向看第 7列，其交叉位置上的数为1，说明这两列的交互作用列为第1 列。值得注意的是，交互作用项的自由度为两个因素的自由度之积，每个二水平因素的自由度都为1，因此两个二水平因素的交互作用项仅占 1 列；两个三水平因素的交互作用项的自由度为2×2=4，因此两个三水平因素的交互作用项需占 2 列；同理，两个四水平因素的交互作用项需占用 3 列，依此类推[1]。

根据表1和表 2，就可以进行表头设计了。将反应温度 A 放在L8（27）表的第 1 列，反应时间 B 放在第 2 列。然后查交互作用表，可知反应温度与反应时间的交互作用AB 应落在第 3 列，因此第 3 列不能再安排其他因素，否则会产生混杂。于是可把磺酸浓度 C 放在第 4 列，操作方法 D 可以放在5、6、7 三列中任何一列上，不妨将 D 放在第 7 列上。这样就完成了该实验的表头设计，如表 3所示。

表3 用 L8（27）正交表安排乙酰苯胺磺化实验的表头设计

完成表头设计之后，将 L8（27）表中的第 1、2、4、7列摘录出来，将表中的代码 1、2 转化成 4个实验因素的真实水平，然后按照表中的实验点安排实验，得到实验结果见表4。

表4 L8（27）正交设计的实验结果

对该资料进行分析的SAS 程序如下：

data prg1;input a b c d y@@;cards;111165 112274121271 122173211270 212173221162 222267;run;proc glm data=prg1;class a b c d;model y=a b c d a*b;run;

程序说明：数据步建立数据集 prg1，变量 a、b、c、d、y 分别代表反应温度、反应时间、磺酸浓度、操作方法和结果变量收率。这里各个因素的取值是用正交表中的水平代码1、2 表示的，这样表示的优点是写起来比较简单。当然也可以采用各个因素的真实水平，只不过输入时会繁琐一些。需要注意的是，交互作用列和空白列中的数字是不出现在数据集中的。与其他各种设计类型的定量资料一样，进行正交设计定量资料的方差分析时仍然采用 GLM 过程。在class语句中，指定分组变量为a、b、c、d。使用 model 语句指定模型的具体形式，该语句等号左端为结果变量 y，等号右端为需要分析的效应，包括四个主效应和一个交互效应。

主要输出结果与结果解释：

The GLM procedure dependent variable: y

以上是对整个模型进行假设检验的结果，输出内容包括自由度、离均差平方和、均方、F 值和P 值，其中 F=11.82、P=0.0798。

R-square Coeff var Root MSE y Mean 0.967276 2.101244 1.457738 69.37500

以上是一些描述性统计量，R-square 为决定系数，Coeff var 为变异系数，Root MSE 为误差均方的平方根，y Mean为结果变量的均数。

Source DF Type III SS Mean square F value Pr ＞F a 1 15.12500000 15.12500000 7.12 0.1165 b 1 10.12500000 10.12500000 4.76 0.1607 c 1 45.12500000 45.12500000 21.24 0.0440 d 1 10.12500000 10.12500000 4.76 0.1607 a*b 1 45.12500000 45.12500000 21.24 0.0440

以上是对各个效应进行假设检验的结果，其中因素 A对应的F=7.12、P=0.1165；因素 B和因素 D 对应的F=4.76、P=0.1607。这三者对于结果变量的作用没有统计学意义。因素 C 与交互作用 AB 对应的F=21.24、P=0.0440＜0.05，这两项对结果变量的作用有统计学意义。根据上述结果可知，磺酸浓度、反应温度与反应时间的交互作用对产物的收率存在影响，而反应温度、反应时间及操作方法对收率没有影响。还可对 P ＞0.05的项进行逐一淘汰，通常从最大 P 值对应的项开始淘汰，直到所有项对应的P 值都小于0.05 为止。

对正交设计的定量资料除了进行方差分析外，还可以通过简单的计算进行直观分析，直观分析包括综合比较和极差分析。综合比较是指比较不同因素各水平的结果大小，筛选全部因素水平最佳组合条件，此时可不必做复杂的方差分析。一个因素的极差是指该因素各水平均值的最大值与最小值之差，极差值越大，说明改变这一因素的水平会使结果产生较大的变化[2]。极差分析就是比较各因素极差的大小，可以区分因素的主次。现将例1 中不同因素的两个水平的实验结果分别求和，具体见表5。

表5 L8（27）正交设计的直观分析计算表

表5 中 T1m为第 m 列水平数为1 时实验结果的合计，T2m为第 m 列水平数为2 时实验结果的合计。例如，反应温度 A 为1 水平，也就是 50 ℃ 时实验结果的合计为283，其为2 水平时实验结果的合计为272。

根据表 5 中的数据进行综合比较，由于T11（283）＞T21（272），说明反应温度 50 ℃ 比 70 ℃ 时的产物收率高；T12（282）＞T22（273），说明反应时间 1 h 比 2 h的产物收率高；T13（268）＜T23（287），说明反应温度和反应时间存在交互作用；T14（268）＜T24（287），说明磺酸浓度 27%比 17% 时的产物收率高；T17（273）＜T27（282），说明不搅拌比搅拌时的产物收率高。单因素分析的结论为：反应温度 50 ℃、反应时间 1 h、磺酸浓度 27%、操作方式为不搅拌时收率较高。但是因为反应温度和反应时间存在交互作用，还需再按表 5 第 1、2 两列计算 A、B 两个因素不同水平组合下收率的合计：

反应温度A反应时间 B 50 ℃ 70 ℃1 h 65 + 74=139 70 + 73=1432 h 71 + 73=144 62 + 67=129

4 种水平组合下的合计结果显示，反应温度 50 ℃ 与反应时间 2 h的收率最高，这与单因素分析的结论并不一致，所以反应温度 50 ℃、反应时间 2 h、磺酸浓度 27%、操作方式为不搅拌是最佳组合条件[4]。同时也可以看出，这个组合条件在本次研究中并没有安排进行实验。

由表 5 可以算得 A、B、C、D 这 4个实验因素的极差分别为RA=2.75、RB=2.25、RC=4.75、RD=2.25，RC＞RA＞RB=RD，所以磺酸浓度是主要因素，反应温度次之，反应时间和搅拌方式是最次要的因素。

例2 在一项微生物培养液成分的优化实验中，希望找出最优的培养液成份，欲考虑的因素及其水平见表6。已知交互作用 AC 存在的可能性极大，AB和AE 存在的可能性不大，但无把握断定其不存在，希望通过实验加以考察[5]。

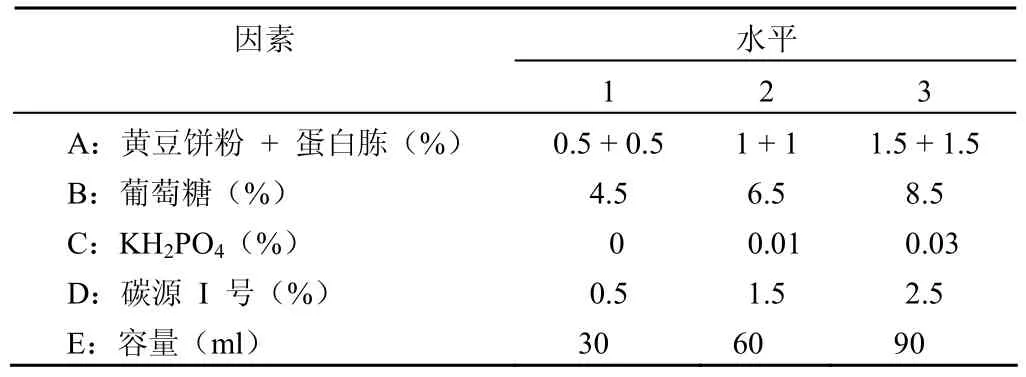
表6 培养液优化实验的因素水平表

表7 L27（313）正交表

正交设计的实施：本实验涉及5个三水平的实验因素，若进行析因设计，则至少需要做 35×2=486 次实验，实验次数过多。由于只需要考虑 3个一阶交互作用，故适合采用正交设计。

本例中每个实验因素的自由度都为2，5个因素的自由度为10；每个交互作用的自由度为2×2=4，3个一阶交互作用的自由度为12；总的自由度为22。在三水平正交表中，每一列的自由度为2，故需要 11 列来安排实验因素及其交互作用。采用 L27（313）正交表安排此实验是可行的，因为此表共有 13 列，5个因素占用 5 列，3个一阶交互作用占用 6 列，还剩两个空列用于估计实验误差，具体见表7。同时，假设已经得到了现有的L27（313）正交表的表头设计表，具体见表8。

表8 L27（313）正交表的表头设计表

在表 8 中，每个实验因素占 1 列，每个一阶交互作用占 2 列，例如因素 A 与B的交互作用 AB 占用第 3 列和第 4 列，分别用 AB1和AB2表示。根据此表头设计，可以直接将各因素安排到相应的列中，然后摘录出单个实验因素对应的列，将各列的水平代码转换成实验因素的真实水平。限于篇幅，经转换后的表格不再给出，仅将实验结果列于表 7 中。

对该资料进行分析的SAS 程序如下：

data prg2;input a b c d e y@@;cards;111110.69112220.54113330.37121320.66122130.75123210.48131230.81132310.68133120.39211110.93212221.15213330.90221320.86222130.97223211.17231230.99232311.13233120.80311110.69312221.10313330.91321320.86322131.16323211.30331230.66332311.38333120.73;run;proc glm data=prg2;class a b c d e;model y=a b c d e a*c a*b a*e;run;proc glm data=prg2;class a b c d e;model y=a b c d e a*c;run;

程序说明：数据步建立数据集 prg2，与例1 一样，这里各个因素的取值仍然采用正交表中的水平代码 1、2、3 表示。在L27（313）正交表中，因素 E和因素 D 分别位于第 8 列与第 11 列，E的位置在D 之前，所以输入数据时要注意它们的顺序。本例使用了两个 GLM 过程步，两者的不同之处在于第二个 GLM 过程去掉了交互作用项AB 与AE。

主要输出结果与结果解释：

Source DF Sum of squares Mean square F value Pr ＞F Model 22 1.75077037 0.07958047 4.97 0.0651 Error 4 0.06408148 0.01602037 Corrected total 26 1.81485185 Source DF Type III SS Mean square F value Pr ＞F a 2 0.89516296 0.44758148 27.94 0.0045 b 2 0.05031852 0.02515926 1.57 0.3138 c 2 0.23000741 0.11500370 7.18 0.0475 d 2 0.06667407 0.03333704 2.08 0.2402 e 2 0.10738519 0.05369259 3.35 0.1397 a*c 4 0.30961481 0.07740370 4.83 0.0781 a*b 4 0.04577037 0.01144259 0.71 0.6239 a*e 4 0.04583704 0.01145926 0.72 0.6233

以上是第一个 GLM 过程的主要输出结果，对整个模型进行假设检验的F=4.97、P=0.0651。在各个效应项的检验结果中，因素 A 对应的F=27.94、P=0.0045；因素 C对应的F=7.18、P=0.0475。这两者的作用都有统计学意义。交互作用 AC的P 值接近于0.05的临界水平。交互作用 AB 与AE 没有统计学意义，结合实验之前已经掌握的情况，将 AB 与AE 去掉之后重新拟合模型。

Source DF Sum of squares Mean square F value Pr ＞F Model 14 1.65916296 0.11851164 9.13 0.0002 Error 12 0.15568889 0.01297407 Corrected total 26 1.81485185 Source DF Type III SS Mean Square F value Pr ＞F a 2 0.89516296 0.44758148 34.50 ＜0.0001 b 2 0.05031852 0.02515926 1.94 0.1863 c 2 0.23000741 0.11500370 8.86 0.0043 d 2 0.06667407 0.03333704 2.57 0.1178 e 2 0.10738519 0.05369259 4.14 0.0430 a*c 4 0.30961481 0.07740370 5.97 0.0070

以上是第二个 GLM 过程的输出结果，对整个模型进行假设检验的F=9.13、P=0.0002。在对各个效应的检验中，因素 A、C、E 以及交互作用 AC 都有统计学意义，其 P 值分别为＜0.0001、0.0043、0.0430、0.0070；因素 B与D的作用没有统计学意义。最好，将 B、D 淘汰后再进行分析，以得到更稳定的计算结果，此处从略。

[1]Hu LP.Application of statistical triple-type theory in the experiment design.Beijing: People’s Military Medical Press, 2006:121-132.(in Chinese)胡良平.统计学三型理论在实验设计中的应用.北京:人民军医出版社, 2006:121-132.

[2]Mao SS, Zhou JX, Chen Y.Design of experiment.Beijing: China Statistics Press, 2004:117-200.(in Chinese)茆诗松,周纪芗, 陈颖.试验设计.北京: 中国统计出版社, 2004:117-200.

[3]Ren LQ.Optimum design and analysis of experiments.2nd ed.Beijing: Higher Education Press, 2003:10-58.(in Chinese)任露泉.试验优化设计与分析.2版.北京: 高等教育出版社, 2003:10-58.

[4]Sun ZQ.Medical statistics.Beijing: People’s Medical Publishing House, 2002:188-194.(in Chinese)孙振球.医学统计学.北京:人民卫生出版社, 2002:188-194.

[5]Wang WZ, Mao SS, Zeng LR.Design and analysis of experiments.Beijing: Higher Education Press, 2004:114-191.(in Chinese)王万中, 茆诗松, 曾林蕊.试验的设计与分析.北京: 高等教育出版社, 2004:114-191.