带相依利率含副索赔风险模型中的几个破产问题
2010-11-26易亚利
易亚利
(1.玉林师范学院 数学与计算机科学系,广西 玉林 537000;2.湖北大学 数学与计算机科学学院,湖北 武汉 430062)
0 引言
经典的风险理论模型分为离散型和连续型,经典离散型风险模型的总索赔过程服从的是复合二项分布,经典连续型风险模型的总索赔过程服从复合泊松过程,Lundberg和Cramér在该模型下得到了众所周知的Lundberg不等式和Cramér-Lundberg近似公式.在求取保费和破产概率的数据等具体的经济应用中我们常常考虑的是离散模型,同时利率往往是一个不可忽略的经济因素,文献[1]研究了常利率下的风险模型,并用鞅方法和递推方法给出了终极破产概率的上界.文献[2]等讨论了利率是独立同分布的风险模型中的系列破产问题.利率在现实生活中常常不是独立同分布的,某时段的利率通常与它前面时刻的利率有着一定的关系,有相依利率的风险模型逐渐成为精算界研究的热点.同时由于突发事件如地震、火灾导致的财产索赔(主索赔)往往连带着医疗等其他索赔(副索赔),因此有必要研究含副索赔的风险模型.本文中考虑了利率{In,n≥1}满足一阶自回归结构且带副索赔的风险模型,得到了其终极破产概率和破产前瞬时赢余分布的上界,为保险公司的实际经营提供了相应的理论依据.
假设在第n时间段有非负的利率In(n≥1),且{In,n≥1}满足一阶自回归结构
In=αIn-1+Mn, n=1,2,…
(1)
其中0≤α<1,I0=i0≥0为一常数,{Mn,n≥1}为相互独立同分布的非负随机变量序列.易知
In=αni0+αn-1M1+…+αMn-1+Mn, n=1,2,….

若保险公司在每个时段初就收到保费Xk,则到第n个时段末的总盈余

(2)

用ψ(u,i)表示初始盈余为u,初始利率为i0的终极破产概率,ψn(u,i0)表示初始盈余为u,初始利率为i0,破产时刻不超过n的概率,则
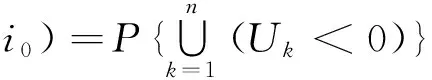
定义保险公司的破产时刻为T=inf{n:n>0,Un<0},并约定infΦ=+∞;用T(u,i0)表示初始盈余为u,初始利率为i0的破产时刻.Fn(u,z,i0)表示初始盈余为u,初始利率为i0,破产时刻为n的条件下,破产前一刻盈余不超过z的概率;F(u,z,i0)表示初始盈余为u,初始利率为i0,破产前一刻盈余不超过z的概率,即

1 终极破产概率的递推公式
首先利用递推方法得到以上模型中ψn(u,i0)的一个递推公式,由该公式可以对第n时段的破产概率进行数值计算,同时也是求取终极破产概率上界的理论基础.
定理1 对于∀n≥1及u≥0,有

(3)

(4)
其中ψ0(u,i0)=I(u≤0).
定理1的证明记h=αi0+m,先证明(3)式.
当n=1时,由(2)式有
U1=(u+X1)(1+I1)-W1=(u+X1)(1+αi0+M1)-W1
(5)
由ψ0(u,i0)的定义知(3)式显然成立.

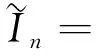
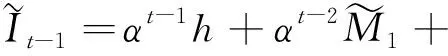
给定W1=w,X1=x,M1=m,则当0≤w≤(u+x)(1+h)时,有U1>0,故由(2)式有
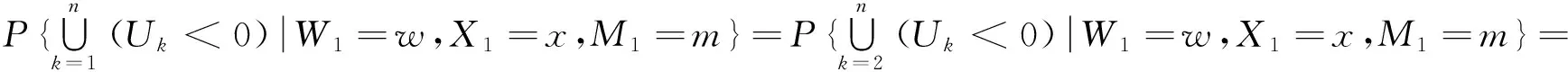
从而对于一般的n,有
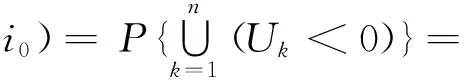

2 终极破产概率和破产前瞬时赢余分布的上界
在有利率的情况下,得到保险公司破产概率的精确解很困难,因此我们转而研究其终极破产概率的上界问题.
定理2 设B(x)是一个NWU函数[1],Λ是一个非负函数,若B及Λ满足



(6)
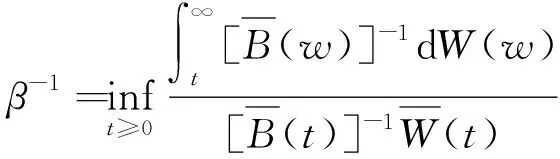
(7)
定理2的证明首先用数学归纳法证明对∀n=1,2,…,有

(8)
由(6)式可得

(9)
当n=1时,由(9)式有
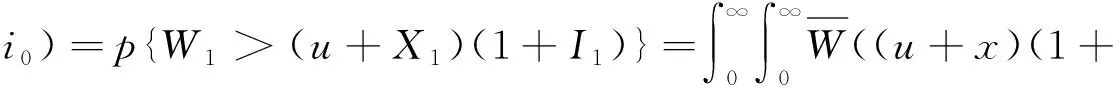
因为B为NWU函数,故
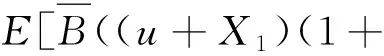
假设当n=k时(8)式成立,则当n=k+1时,由(3)式和(9)式有
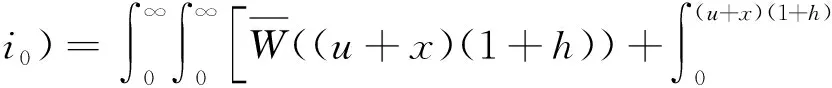
此外,当∀0≤w≤(u+x)(1+h)时,由函数B(·)的假设,可知
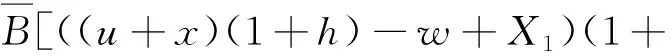
故得到
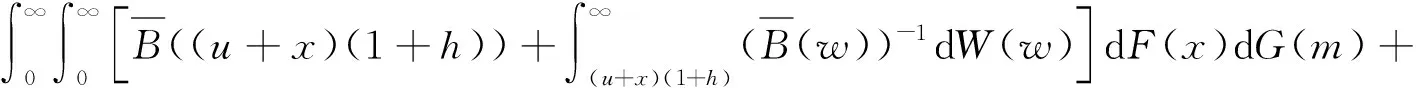
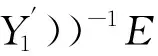
综上所述,对一切n≥1,有(8)式成立,再在(8)式两边令n→∞,即得(6)式,定理2得证.
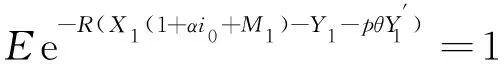
(10)
则有
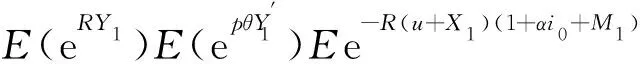
(11)
其中β如定理2中所定义.

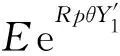
推论2 如果W(w)为一NWUC分布函数,则有ψ(u,i0)≤Ee-R(u+X1)(1+αi0+M1).
注1 当α=0时,模型(2)成为利率独立同分布的模型;当α=0,p=0时,模型(2)成为利率独立同分布且无副索赔的情形,此时定理2即为文献[1]中的定理4.1.
注2 在经典风险模型中,初始赢余为u的终极破产概率φ(u)满足Lundberg上界,即当EX1>EW1时,若存在常数γ满足Ee-γ(X1-W1)=1,则φ(u)≤e-γu.称γ为经典风险模型中的Lundberg系数,该系数的大小决定了破产概率的大小.类似地,(10)式中的R为模型(2)的Lundberg系数.下面的定理将两者的大小作了比较.
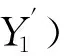
定理3的证明考虑函数g(r)=Ee-r(X1-W1)-1,易知g(0)=0,g′(0)<0,g″(r)≥0,故g(r)是一个凸函数.由(10)式有
1=Ee-R(X1(1+αi0+M1)-W1)≤Ee-R(X1-W1),
即g(R)=Ee-R(X1-W1)-1≥0,又因为g(γ)=0,由函数g(r)的性质可得R≥γ.特别地,如果X1和M1均不退化到0,显然有R>γ.定理3得证.
破产前瞬时赢余的分布是衡量保险公司破产严重性的一个重要指标,有助于保险公司事先采取防范措施避免出现财务困境.
定理4 如果存在一个常数R>0满足Ee-R(X1(1+M1)-W1)=1,
那么
F(u,z,i0)≤βe-R[u(1+αi0)-z]E(e-RuM1)τ(u,i0)+ψ1(u,i0)I(u≤z),

定理4的证明先证Fn(u,z,i0)≤βe-R[u(1+αi0)-z]E(e-RuM1)
(12)
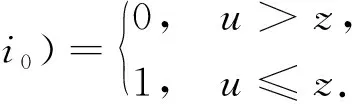
注3 (12)式中的ψ1(u,i0)可由定理1直接计算得到.
参考文献:
[1] Cai J.Discrete time risk models under rates of interest [J].Probability in Engineering and Information Sciences,2002,16:309-324.
[2] Cai J.Ruin probobalities with dependent rates of interest [J].Appl Prob,2002,39:312-323.
[3] Yuan K C,Guo J Y.Ruin probability for time-correlated claims in the compound binomial model [J].Insurance:Mathematics and Economics,2001,29:47-57.
[4] Helene C,David L T,Etienne M.Ruin probobilities in the discrete time renewal risk model [J].Insurance:Mathematics and Economics,2006,38:309-323.
[5] 孙立娟,顾岚.离散时间保险风险模型的破产问题[J].应用概率统计,2002,18(3):293-299.
[6] Gao Q B,Wu Y H,Zhu C H.Ruin probability in risk models with dependent rates of interest[J].Statistics and Probability Letters,2007,77:761-768.
