一道错解题的3种正解

●

(天津水运高级技工学校 天津 300456)

问题设x,y是实数,且x2-3xy+y2=1,求S=x2-xy+y2的取值范围.

错解因为

S=x2-xy+y2=

-(x2-3xy+y2)+2(x2-2xy+y2)=

-1+2(x-y)2,

且由题设条件可知x≠y(否则与条件x2-3xy+y2=1矛盾！),所以S=x2-xy+y2无最小值,只有S>-1,即S∈(-1,+∞).

以上解题过程从表面上看似严谨,但结果却是错误的！其实S不会等于0.因为由S=0,可得x=y=0,这与题设条件x2-3xy+y2=1矛盾！因此S∈(-1,+∞)是错误的,它含有增解S=0.

下面笔者给出以上问题的3种正确解法,供大家参考.

正解1因为

S=x2-xy+y2=

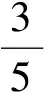
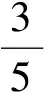
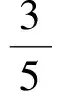
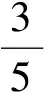
其实,可以由待定系数法顺利获得.

令

S=k(x2-3xy+y2)+[(1-k)x2+

(3k-1)xy+(1-k)y2].

(1)

为了能将中括号内的项配成一个完全平方项,必须满足以下2个条件:

(1)(1-k)(1-k)>0;

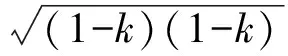
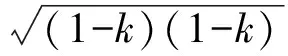
2|1-k|=|3k-1|,

解得

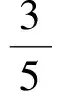
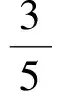
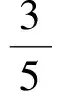
从而

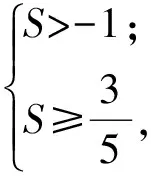
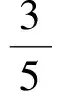
正解2由

1=x2+y2-3xy≥±2xy-3xy,

可得

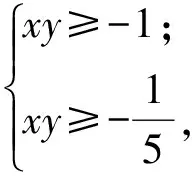
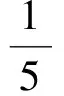
S=x2-xy+y2=x2-3xy+y2+2xy=

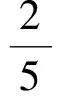
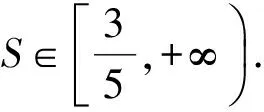
正解3

S=x2-xy+y2,x2-3xy+y2=1.

两式相乘得

(x2-3xy+y2)S=x2-xy+y2,

整理得

(S-1)x2-(3S-1)xy+(S-1)y2=0.

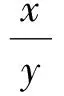
(S-1)t2-(3S-1)t+(S-1)=0.

当S-1=0时,由上式可得t=0,显然有解,故S=1可取.

当S-1≠0时,这时

Δ=(3S-1)2-4(S-1)2=(5S-3)(S+1)≥0，

解得

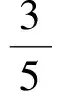
但将条件x2-3xy+y2=1代入S≤-1,可推出

x2+y2≤-2,

显然无实数解,故知S≤-1为增解,应舍去.