返璞归真 回归本源——从一道高考试题谈起

●

(诸暨中学 浙江诸暨 311800)

2010年浙江省数学高考试题以其独具匠心的构思、立意新颖的设问给人以耳目一新的感觉.但是从学生反馈的信息来看，答题情况却不尽人意，从中反映出的问题值得深思.本文以2010年浙江省数学高考理科第21题为例，结合笔者对部分考生和教师的访谈，探讨数学教学中存在的一些问题，并提出几点教学建议,供大家参考.

1 试题及解题错误

下面先给出2010年浙江省数学高考理科试题第21题，根据本文的需要，这里只研究第(2)小题：

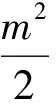
(1)略;

(2)设直线l与椭圆C交于点A,B，△AF1F2,△BF1F2的重心分别为G,H,若原点O在以线段GH为直径的圆内，求实数m的取值范围.

这是一道常规的解析几何题目，考查了直线与椭圆的位置关系、点与圆的位置关系等基础知识以及解决解析几何问题的基本思想和方法.按照常理，解决这一问题并不十分困难，但根据调查发现，本题的得分率并不理想，主要有以下几种错误类型.

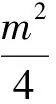
类型3缺乏必要的转化与化归的能力，导致复杂的计算，最终没能解出答案或者因为计算错误导致了错误的答案.在得出了重心坐标之后，接下来的工作就是利用已知条件“原点在以GH为直径的圆内”得出一个关于m的不等式，并由此求出范围.对于这一条件，不同的学生可能有不同的处理方法，这里引用几种最典型的做法：

(1)求出圆的方程，先将点O的坐标代入方程的左端，再将“等号改成小于号”即可.

(2)设GH的中点为M，则2|OM|<|GH|,从而

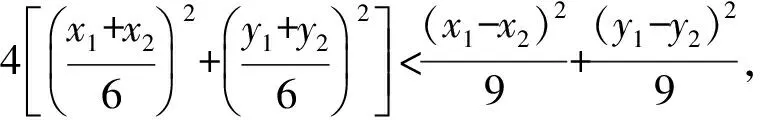
然后化简可得

x1x2+y1y2<0.

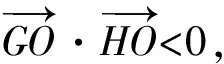
x1x2+y1y2<0.

不难看出，这几种处理方法从运算量来讲有很大的差异，第3种做法将已知条件进行了合理地等价转化，大大减少了运算量.

类型4忽视题目的隐含条件，导致解题失误.事实上，本题中m的范围由2个条件决定:一个是原点在以GH为直径的圆内，另一个是隐含条件“直线与椭圆有2个不同的交点”.对于后者，很多学生并没有注意到.

2 产生问题的原因

根据前文所述的解题错误可以看出，考生在解决本题时出错的主要原因是：

(1)过度依赖解题模式，导致思维僵化，忽视题目中蕴含的数学关系.

(2)重结果、轻过程，缺乏积极思维的习惯和主动性，例如重心坐标，很多考生实际上具备推导这一结果的能力，只是没有主动去思考如何推导.

(3)思维的灵活性不够，缺乏必要的等价转化与化归的能力，对于题目的条件只能直接应用，不能举一反三.

那么，从教学的角度看，产生问题的主要原因是什么呢？当然,原因是多方面的，但是笔者以为，以下几点是最主要的.

2.1 将数学教学异化为题型总结,抑制了学生思维能力的发展

新课程意义下的数学课堂教学要保证学生有足够的时间和机会建构性地接触、认识数学，从而理解数学、运用数学.既要重视数学概念的发生过程，也要重视数学知识的应用.但是，从教学的实际来看，重结果、轻过程，忽视数学的本质，将数学教学的主要精力放在题型总结上，数学课堂被异化为题型教学.诚然，模式识别策略是解题活动最重要的策略之一，积累一定的解题经验，总结必要的解题模式是提高解题能力的必要条件.但是在教学实践中，有些教师过分强调模式化，将数学问题归纳成很多的“类型”，然后对每一种“类型”都总结出一定的解题规则，而对于隐含于模式背后的数学思想却重视不够，似乎学生只要掌握了这些规则，便能在解决问题时“有法可依”，这种做法在一定程度上助长了学生对解题模式的依赖.

2.2 教学过程中，“快节奏、大题量”剥夺了学生思考的机会

不可否认，在新课程改革逐步深入的背景下，课堂教学的研究得到了广泛地重视，也涌现出了一大批优秀的课例.但是不容忽视的是，在实际的教学工作中，特别是高考复习课教学中，“大容量、快节奏，在最少的时间里讲授最多的题目”占据了一定的市场，甚至是一种“流行色”.这种课堂的实际情况是，学生来不及思考，就被告知解题的思路和方法，学生的任务只是接受、记忆、积累题型和方法，至于为什么要这样解题？为什么会这样思考？这些问题都来不及探究.这样下去的结果可想而知，学生在课堂上失去了思考的机会，思维能力得到培养的权利也一并失去了.就解析几何的教学而言，广大考生的训练不可谓不多，但是效果却难如人意.

2.3 大量的重复训练降低了学生数学思维的积极性

正如张奠宙教授指出的那样，“深受科举文化影响的中国数学教育，有着独特的考试文化”，维系着考试文化的一个常见学习活动就是操练.似乎创造也从熟习而来，古训说了，“熟能生巧”嘛！文献[1]至文献[3]彻底颠覆了这一千年古训.过度的重复训练不但不能生巧，还会助长学生厌学的情绪.同时，大量机械化的解题活动，使得学生的思维趋于僵化.当然，我们并不反对必要的练习，但是除了练习还要关注哪些问题，就是我们必须要考虑的问题了.

3 对教学工作的启示

针对以上教学中出现的问题，笔者提出以下教学建议.

3.1 返璞归真，重视概念的发生过程，还原数学课堂的本来面目

在数学教学过程中，返璞归真、还原数学课堂的本来面目是必由之路，让数学课堂成为教师引导下的数学探究活动.在活动中，一方面学生掌握数学知识，同时思维能力和思维品质得到训练和提高，情感、价值观得到必要的陶冶，这些目标都要得到足够的重视.“1个定义、2点注意、3个例题”曾经是非常流行的教学模式，对概念的发生过程缺乏必要的展示，直接告知定义，然后举例识别就可以了.相比概念，更重要的似乎是例题，这些作法必须在教学过程中进行纠正.

3.2 重视学生的思维过程

培养学生思维能力的主阵地是数学课堂.教师在课堂上要给学生足够的时间和机会思考数学问题，要重视学生的思维过程.通过对学生思维过程的剖析和评价，促使学生思维能力的发展和提高.同时，教师也要注重自己思维过程的展示，就象波利亚所说的那样，“与其给人以死板的知识，不如给人以生动、活泼的方法，点石成金的策略、手段.”

3.3 淡化模式识别，重视思想方法

在学生的学习过程中，所积累的经验经过加工，会得出有长久保存价值或基本重要性的典型结构与重要类型——模式，将其有意义地记忆下来，并作有目的的简单编码.当遇到新的问题时，我们可以辨认它属于哪一类基本模式，联想起一个已经解决的问题，以此为索引，在记忆的贮存中提取出相应的方法来加以解决，这就是模式识别的解题策略.不可否认，模式识别是必要的，但是在教学中，一定要跳出模式的圈子，挖掘模式背后蕴含的思想方法，培养学生的数学思维能力，而不是停留在一招一式的所谓技巧上.前文所述的解析几何问题，有很多学生就是因为机械地应用了模式，而且只停留在模式识别的层次，对题目蕴含的数学关系缺乏应有的分析，不能用函数与方程的思想思考问题，从而解题失败.

3.4 重视变式教学，培养学生的思维活性

近年世界各地对儒家文化圈学习理论的探索很是热切，其中注重变式教学是一个非常明显的优点，其实数学向来强调触类旁通、举一反三，改变问题中一些条件变成一道新的题目是常见的培养解决问题能力的作法，即变式教学.Leung[5]更指出这种“解决问题←→编拟一道新题”的循环可以培养学生自我学习的能力.另外，笔者也坚信，得当的变式教学对培养学生思维的灵活性有着不可替代的作用.前文所述的解析几何题，如果在平时的教学过程中，注重了变式训练，注重了题目条件中各种等价形式的转化，学生就可以少走很多弯路.

3.5 引导学生学会思考，养成良好的思维习惯

正如《学会生存》一书中指出的那样，教育具有培养创造精神和压抑创造精神的双重力量，也就是好的教育能够充分施展培育创新的力量，提升受教育者的创新素养，而不当的教育可能构成对创新的打击与窒息.从这个意义上讲，如何在数学教育中，激发学生的创新精神，培养他们勤于思考、善于思考的思维品质是每个数学教师必须要考虑的问题，这大概也是培养能力和提高考试成绩的一个结合点吧.

[1] 李士锜.熟能生巧吗?[J].数学教育学报，1996,5(3):46-50.

[2] 李士锜.熟能生笨吗?——再谈“熟能生巧”[J].数学教育学报，1999,8(3):15-18.

[3] 李士锜.熟能生厌吗?——三谈“熟能生巧”[J].数学教育学报，2000,9(1):23-27.