点击概率问题求解时的常见错误
2010-08-27张禹水鄞州中学浙江宁波315000
●张禹水 (鄞州中学 浙江宁波 315000)
概率知识是高中数学新课程新增加的内容,也是排列、组合知识的应用及延伸.学生在学习过程中普遍感觉概率问题比较抽象、难以理解.在解题过程中也往往会因为概念理解不透、审题不严、考虑不周或忽视公式成立的条件等等而出现错误.为此,笔者对概率问题中学生易犯的错误作如下归纳总结,供读者借鉴与参考.
类型1 “等可能”与“非等可能”概念混同
例1 将一枚骰子连续抛掷2次,所得点数之和等于5的概率是多少?
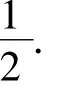

剖析将一枚骰子连续抛掷2次,有36种等可能事件:


例2 某人有5把钥匙,其中有1把是办公室的抽屉钥匙,但他忘了是哪一把,于是他便将5把钥匙逐把地不重复试开.问恰好第3次打开抽屉的概率是多少?
错解5把依次逐把试开,相当于5把钥匙在5个位置的全排列,即n=.“第3次打开”即是第3次已经打开,只需考虑第1次和第2次的情形,则 m=,所以
剖析由等可能事件的概率定义知:n为一次试验中所包含的所有基本事件数,m为此试验中事件A所包含的基本事件数.从集合的角度看:在一次试验中,等可能出现n个结果组成一个集合U,这n个结果就是集合U的n个元素;包含m个结果的事件A对应于U的含有m个元素的子集A.因此事件A的概率是子集A的元素个数与集合U的元素个数的比值.在错解中取n=,是把“5把钥匙依次逐把打开”作为“一次试验”,但取m=,是把事件A作为“第3次恰好打开情形下前3个位置的排列”,显然前后两者不是同一试验类型.从集合角度看,此时A也不是U的子集,所以解答错误.正确解法如下:
5把钥匙依次逐把试开,相当于5把钥匙在5个位置的全排列,即n=,“恰好第3次打开”说明抽屉钥匙固定在第3个位置,因此m=,所以
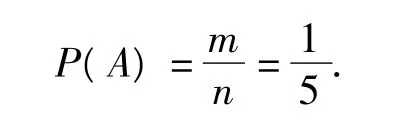
若强调“第3次恰好打开”的情形,则“一次试验应确定为前3次试开中,抽屉钥匙在第3个位置,得 n=A35,m=A24,所以
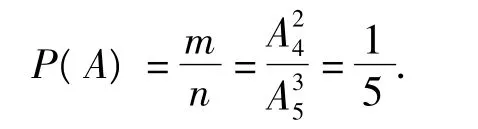
类型2 “有序”与“无序”概念混同
例3 甲、乙2人参加普法知识竞赛,共有10道不同的题目,其中选择题6道,判断题4道,甲、乙2人依次各抽取1道题.
(1)甲抽到选择题、乙抽到判断题的概率是多少?
(2)甲、乙2人至少有1人抽到选择题的概率是多少?
(2)设甲、乙2人至少有1人抽到选择题为事件A,则甲、乙2人都未抽到选择题为事件.由对立事件的计算公式,得
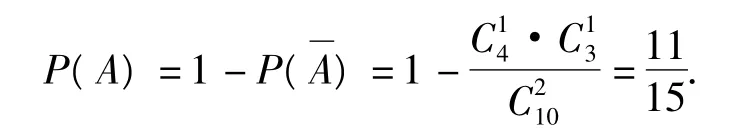
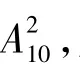
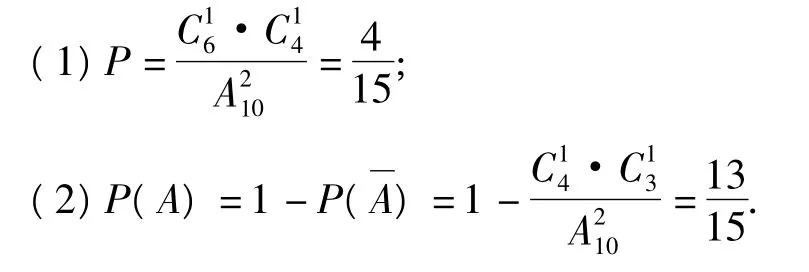
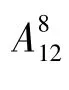
剖析本题中把“12个停车位停8辆车”作为一次试验,计算n时把停车方法按有序进行,即作为排列问题处理.而在计算m时仅考虑4个空位相连而没有考虑8辆车的有序排放问题,即作为组合问题处理.由等可能事件概率意义知,前后两者不是同一试验类型,因此解答错误.正确解法如下:
要正确解决有关概率问题,必须充分理解概率的定义,在解题时要认真分析题意,确实把握n与m的意义,这样才能正确解题.
类型3 “互斥事件”与“独立事件”概念混同
例5 甲、乙、丙3名射手击中目标的概率分别为0.7,0.8,0.85.若他们 3 个人分别向目标发射1枪,试求3弹都脱靶的概率.
错解设甲发射1枪击中目标为事件A,乙发射1枪击中目标为事件B,丙发射1枪击中目标为事件C,则甲、乙、丙3人分别向目标发射1枪击中目标为事件ABC,从而甲、乙、丙3人分别向目标发射1枪击中目标的概率为:
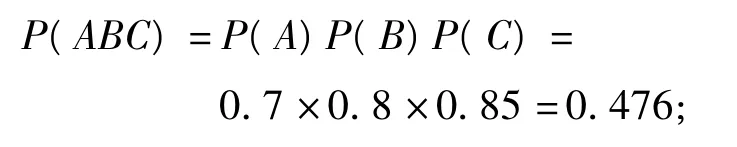
因此3个人分别向目标发射1枪3弹都脱靶的概率为:
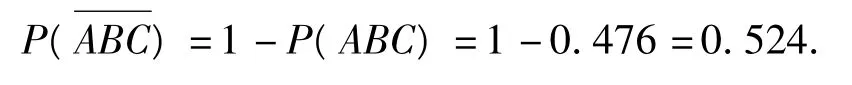
剖析上述错误在于将相互独立事件同时发生的事件当成互斥事件来考虑,认为“3弹都未中”的对立事件是“3弹都中”.而事实上,这两者不是对立事件.正确的解法应为:
甲、乙、丙脱靶的概率分别为

因此3弹都脱靶的概率是
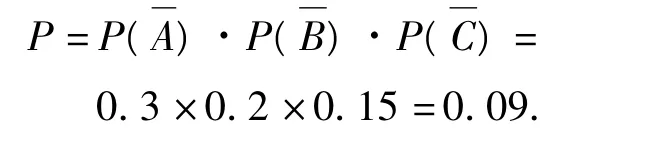
例6 甲投篮命中率为0.8,乙投篮命中率为0.7,每人投3次,2人恰好都命中2次的概率是多少?
错解设“甲恰好投中2次”为事件A,“乙恰好投中2次”为事件B,则2人都恰好投中2次为事件A+B,于是

剖析本题错误的原因是把相互独立并同时发生的事件当成互斥事件来考虑,将2人都恰好投中2次理解为“甲恰好投中2次”与“乙恰好投中2次”的和.互斥事件是指2个事件不可能同时发生;2个事件相互独立是指一个事件的发生与否对另一个事件发生与否没有影响.它们虽然都描绘了2个事件间的关系,但所描绘的关系根本不同.正确解法如下:
设“甲恰好投中2次”为事件A,“乙恰好投中2次”为事件B,且A,B相互独立,则2人都恰好投中2次为事件A·B,于是
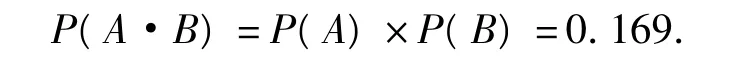
类型4 “互斥事件”与“对立事件”概念混同
例7 甲、乙2名同学分别解1道数学题,每个人解出这道题的概率都是0.6,求至少有1个人解出这道题的概率.
错解甲、乙2人都解不出题的概率都是1-0.6=0.4,从而2位同学都解不出的概率是0.4+0.4=0.8,因此至少有1个人解出的概率为1-0.8=0.2.
剖析上述错解的原因是把“互斥事件”与“对立事件”混同,互斥事件与对立事件的联系与区别主要体现在以下3个方面:
(1)2个事件对立,则必定互斥,但互斥并不一定对立;
(2)互斥的概念适用于多个事件,但对立的概念只适用于2个事件;
(3)2个事件互斥只表明这2个事件不能同时发生,即至多有1个发生,但也可以2个都不发生,而对立事件则表示它们有且只有1个发生.
因此,上述问题的正确解法应为:
甲、乙2名同学解出这道题的概率分别为
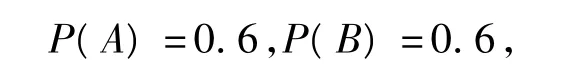
甲、乙2名同学解不出这道题的概率分别为
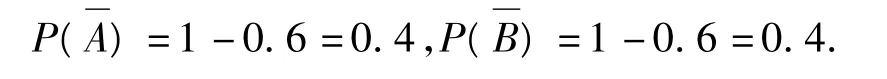
因此甲、乙都解不出这道题的概率为

至少有1个人解出_这道题的概率是

例8 已知8支球队中有3支弱队,以抽签方式将这8支球队分为A,B两组,每组4支.求:
(1)A,B两组中有1组恰有2支弱队的概率;
(2)A组中至少有2支弱队的概率.
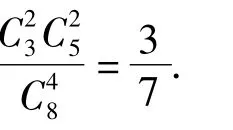
(2)A组中至少有2支弱队包含2种情形,即A组中有2支弱队而B组中有1支弱队,或者A组中有3支弱队而B组中没有弱队.由互斥事件概率的定义,得A组中至少有2支弱队的概率是
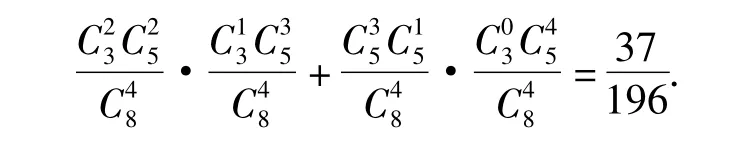
剖析在错解(1)中利用的是等可能事件概率的计算,但在计算过程中忽视了“A,B两组中有1组恰有2支弱队”有2种情形,即A组有2支弱队或B组有2支弱队的情形.在(2)中混淆了互斥事件与对立事件的概念,A组中有2支弱队与B组中有1支弱队不是对立事件,而是同一件事件,因此出现了错误.正确解法如下:
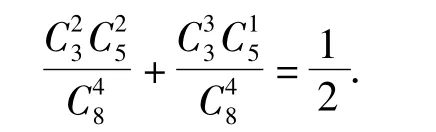
本题着重介绍了较为复杂的等可能事件的概率计算方法和计算过程中容易出现的错误.这类问题一般有3种解法:(1)直接运用公式和已学过的排列组合知识求出;(2)将复杂的事件分成几个互斥事件,然后利用概率加法公式来解决;(3)类似于排列组合的间接法,先求出对立事件的概率,再求所求事件的概率,“至多至少”问题或多元复杂问题用这种方法较简捷.这3种方法都是常用方法,必须熟练掌握.
