一个重要不等式的简证与求商法的应用
2010-11-23陇南师范高等专科学校数学系甘肃成县742500
中学教研(数学) 2010年6期
● (陇南师范高等专科学校数学系 甘肃成县 742500)
一个重要不等式的简证与求商法的应用
●东洪平(陇南师范高等专科学校数学系 甘肃成县 742500)
1 问题的提出及其证明
文献[1]提出了一个重要不等式:
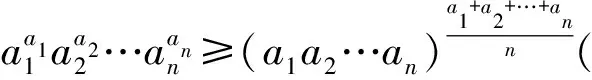
文献[1]用数学归纳法证明了这个不等式,笔者发现可用求商法证明这个不等式,其证明过程更简单易懂,现证明如下.
证明求商.
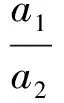
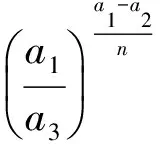
即
因此
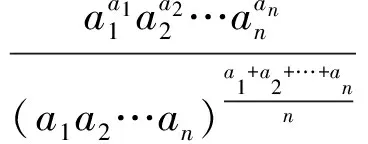
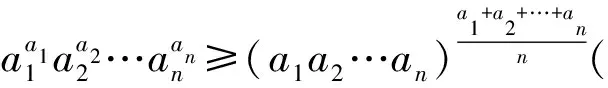
2 求商法及其应用
当一个不等式(或等式)的2边是积的形式时,可用求商的方法去证明其成立,这是数学中最常用的方法——求商法.用求商法去证明上面的重要不等式,其证明过程简单、易懂.数学竞赛中有几个不等式是上面重要不等式的特殊情形,如果不知道上面的重要不等式,这样的不等式该怎样证明呢?那还是用求商法最好!请看下例.
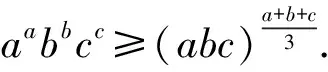
(第3届美国数学奥林匹克试题)
(显然,这是上面重要不等式当n=3时的特殊情形.)
证明(用求商法)
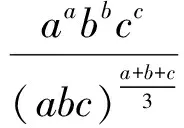

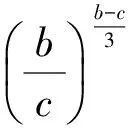
即
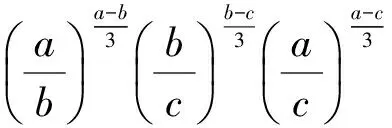
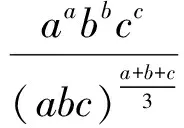
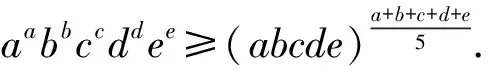
(1979年青海省中学数学竞赛试题)
(显然,这是上面重要不等式当n=5时的特殊情形.)
证明(用求商法)
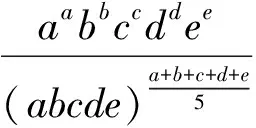

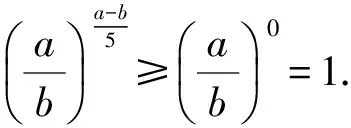
同理可得
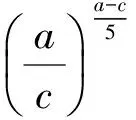
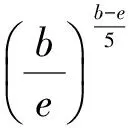
即
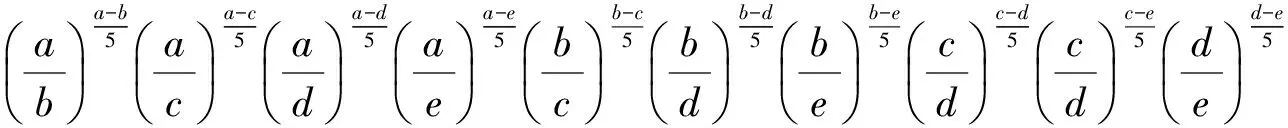
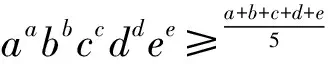
下面再举2个用求商法证明不等式的例子.
例3若a>b>c>0,求证:a2ab2bc2c>ab+cbc+aca+b.
(1978年上海市数学竞赛第二试试题)
证明(用求商法)

即
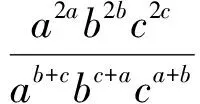

证明(用求商法)
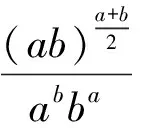

当我们在证明一个数学命题时,首先想到的是最常用的方法.如果能用最常用的方法证明这个数学命题,而且证明过程简单易懂,那么这样的证明方法就可称得上是好方法.因此,我们千万不能把最常用的方法忘掉!
[1] 赵生筱.一个平均值不等式[J].数学通报,2002(7):21-22.
