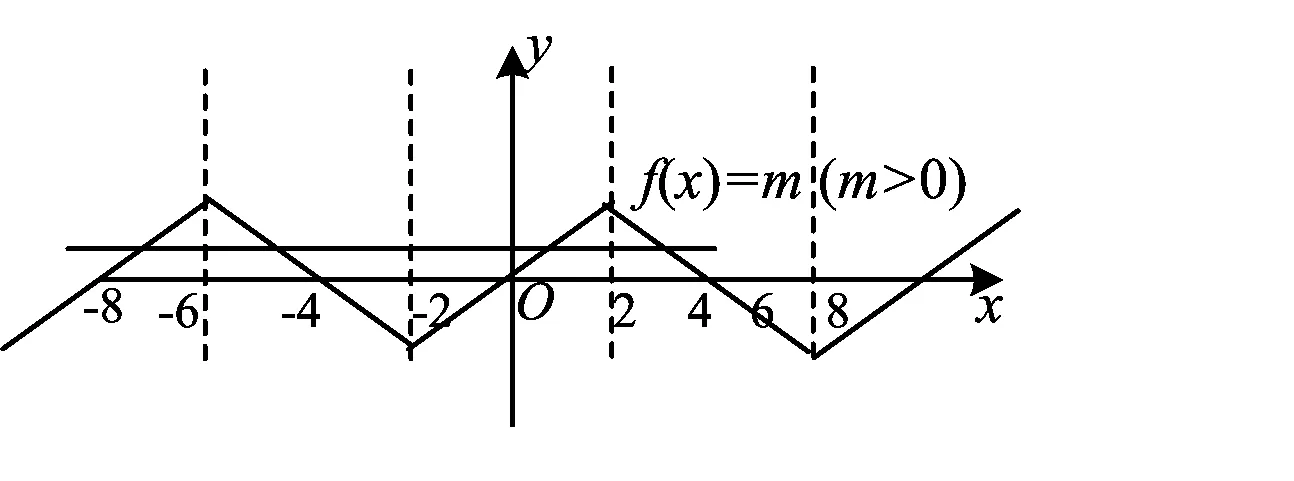抽象函数的对称性与周期性刍议

● (鄞州区五乡中学 浙江宁波 315111)

抽象函数的对称性与周期性刍议

●王国云(鄞州区五乡中学 浙江宁波 315111)

抽象函数的对称性与周期性一直是数学高考考查的一个难点和热点，也是函数教学中一类综合性比较强的问题．这类问题往往只给出函数的特征或性质，只有通过分析、推理、归纳和类比来研究它，因而它们具有抽象性、综合性、技巧性等特点．解决这类问题时必须掌握函数的基础知识、具有抽象思维能力和综合应用数学知识解决问题的能力．本文对抽象函数的对称性与周期性的有关特征进行归纳整理，便于从无形到有形对抽象函数的图像特征与性质有比较清晰的认识，克服抽象恐惧的心理，提高解决抽象函数问题的能力．

1 抽象函数的对称性与周期性的某些重要特征

1．1 抽象函数的对称性

1.1.1 有关轴对称问题

我们知道，若函数f(x)满足f(-x)=f(x)⟺y=f(x)是偶函数⟺y=f(x)的图像关于直线x=0对称(假设定义域为R，下同)，则有下列结论成立：

结论1f(a+x)=f(a-x)⟺y=f(x)的图像关于直线x=a对称；或f(2a+x)=f(-x)⟺y=f(x)的图像关于直线x=a对称．

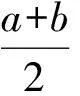
1.1.2 有关中心对称问题

我们知道，若函数f(x)满足f(-x)=-f(x)⟺y=f(x)是奇函数⟺y=f(x)的图像关于点(0，0)对称，则显然还有下列结论结成立：

结论3f(a+x)=-f(a-x)⟺y=f(x)的图像关于点(a,0)对称；或f(a+x)+f(a-x)=0⟺y=f(x)的图像关于点(a,0)对称．

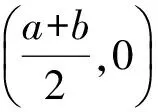
结论6若函数y=f(x)满足条件：

f(a+x)=f(a-x)或f(a+x)=-f(a-x)，

且方程f(x)=0有n个根，则此n个根的和为na．

1.2 抽象函数的周期性

我们知道，若函数f(x)满足f(x+T)=f(x)⟺常数T是函数y=f(x)的一个周期，则有下列结论结成立：

结论7f(x+a)=f(x-a)⟺y=f(x)的周期为2a．

结论8f(x+a)=f(x-b)⟺y=f(x)的周期为a+b．

结论9f(x+a)=-f(x-b)⟺y=f(x)的周期为2(a+b)．

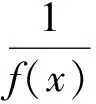
1.3 双对称与周期性的关系

函数f(x)还存在如下一些性质：

结论11若函数y=f(x)的图像关于直线x=a与x=b(a≠b)对称，则y=f(x)是以T=2(b-a)为周期的周期函数．

结论12若函数y=f(x)的图像关于点(a,0)与(b,0)(a≠b)对称，则y=f(x)是以T=2(b-a)为周期的周期函数．

结论13若函数y=f(x)的图像关于直线x=a与点(b,0)(a≠b)对称，则y=f(x)是以T=4(b-a)为周期的周期函数．

推论1若函数y=f(x)的图像关于直线x=a(a≠0)对称且f(x)是偶函数，则函数f(x)的周期T=2a.

推论2若函数y=f(x)的图像关于直线x=a(a≠0)对称且f(x)是奇函数，则函数f(x)的周期T=4a．

2 抽象函数的对称性与周期性应用举例

例1已知定义在R上的奇函数f(x)，满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则

( )

A.f(-25)

B.f(80)

C.f(11)

D.f(-25)

(2009年山东省数学高考文科试题)

解因为f(x)满足f(x-4)=-f(x),所以

f(x-8)=f(x),

即f(x)是以8为周期的周期函数,则

f(-25)=f(-1),f(80)=f(0),f(11)=f(3).

又因为f(x)在R上是奇函数，f(0)=0,所以

f(80)=f(0)=0,f(-25)=f(-1)=-f(1).

而由f(x-4)=-f(x),可得

f(11)=f(3)=-f(-3)=-f(1-4)=f(1).

又因为f(x)在区间[0,2]上是增函数,所以

f(1)>f(0)=0,即-f(1)<0,从而

f(-25)

故选D.

例2函数f(x)的定义域为R，若f(x+1)与f(x-1)都是奇函数，则

( )

A．f(x)是偶函数 B.f(x)是奇函数

C.f(x)=f(x+2) D.f(x+3)是奇函数

(2009年全国数学高考理科试题Ⅰ)

解由f(x+1)与f(x-1)都是奇函数，可得

f(-x+1)=-f(x+1),f(-x-1)=-f(x-1).

因此函数f(x)关于点(1,0)及点(-1,0)对称，是周期T=2[1-(-1)]=4的周期函数，从而

f(-x-1+4)=-f(x-1+4)，

f(-x+3)=-f(x+3),

即f(x+3)是奇函数.故选D.

例3在R上定义的函数f(x)是偶函数，且f(x)=f(2-x)，若f(x)在区间[1,2]是减函数，则函数f(x)

( )

A.在区间[-2,-1]上是增函数，在区间[3,4]上是增函数

B.在区间[-2,-1]上是增函数，在区间[3，4]上是减函数

C.在区间[-2,-1]上是减函数，在区间[3，4]上是增函数

D.在区间[-2,-1]上是减函数，在区间[3，4]上是减函数

(2007年天津市数学高考试题)

解因为在R上定义的函数f(x)是偶函数，且f(x)=f(2-x)，所以

f(-x)=f(x)，f(x+2)=f(-x),

即

f(x+2)=f(x)，

于是f(x)是以2为周期的周期函数.由f(x)在区间[1，2]上是减函数，得f(x)在区间[3，4]上是减函数;又由偶函数的性质可知f(x)在区间[-4,-3]上是增函数，因而f(x)在区间[-2,-1]上是增函数.故选B.

例4已知定义在R上的奇函数f(x)，满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有4个不

同的根x1,x2,x3,x4,则x1+x2+x3+x4=________.

(2009年山东省数学高考理科试题)

图1

解因为f(x)是定义在R上的奇函数，满足f(x-4)=-f(x),所以

f(x-4)=f(-x).

由f(x)为奇函数,得函数图像关于直线x=2对称且f(0)=0.又由f(x-4)=-f(x)知

f(x-8)=f(x),

因此f(x)是以8为周期的周期函数.又因为f(x)在区间[0,2]上是增函数,所以f(x)在区间[-2,0]上也是增函数.如图1所示,方程f(x)=m(m>0)在区间[-8,8]上有4个不同的根x1,x2,x3,x4,不妨设x1

x1+x2=-12,x3+x4=4，

因此

x1+x2+x3+x4=-12+4=-8.