从良好学习方式的形成看数学课堂中有效学习的策略
2010-11-23杭州师范大学附属中学浙江杭州310030
● (杭州师范大学附属中学 浙江杭州 310030)
从良好学习方式的形成看数学课堂中有效学习的策略
●张小群(杭州师范大学附属中学 浙江杭州 310030)
课堂教学的目的在于促进学生的学习与发展,使每一位学生不断地获得新的知识和能力.然而课堂教学的时间是有限的,要实现用最少的时间使学生获得最大的进步与发展,就需要每一位教师对课堂教学做多方面深入的思考和研究.所谓“有效学习”,就是指教师遵循教学活动的客观规律,以尽可能少的时间、精力和物力投入,取得尽可能多的教学效果,从而实现特定的教学目标,满足社会和个人的教育价值需求.在实际教学中,教师应围绕促使学生形成良好的数学认知结构和学习数学的情感系统来实施教学策略,以保证学习活动的顺利进行.采取适宜的教学策略形成良好的学习方式是促进学生有效学习的一个重要方面.如何引导学生形成良好的学习方式是每个教师要思考的问题.下面笔者针对数学课堂教学中进行有效学习的若干策略进行例谈.
1 提供宽广的思维空间,促进学生的研究性学习
新课标的核心理念是以人为本,感悟知识生成的来龙去脉,学生不再是知识生成过程中的“热闹的看客”与“匆匆的过客”,数学课堂是学生研究性学习、展示学生思维活动的主舞台.我们的课堂应该是师生与研究性学习踏歌起舞,让学生尝试数学研究的过程,体验再创造的激情,让数学课堂真正成为知识传授、能力提升、思想交流、智慧碰撞、心灵相约、生命互动的课堂.荷兰著名数学教育家弗赖登塔尔认为:学习数学的唯一正确方法是让学生进行“再创造”.所有的新知识只有通过学生自身再创造,使其纳入自己的认知结构中,才可能成为有效的知识.
研究性学习是以学生的学习为主体,重过程,重发现,重参与,使学生在不断探索中发现问题、分析问题和解决问题,形成自主创新能力的学习形式.笔者认为在课堂中无时无刻不存在着研究性学习的契机,教师应提供给学生宽广的思维空间,才能促进学生的研究性学习.
例1已知直线l经过点A(1,1),若抛物线y2=x上存在2个点关于直线l对称,求直线l的斜率k的取值范围.
在教学时,笔者没有将思路直接告诉学生,而是设置问题,放手让学生探究.
(1)求k的范围的本质是什么(解关于k的不等式)?
(2)根据什么特征来建立关于k的不等式?
这样,教师导而不代,消除了学生的依赖心理,克服了思维惰性,主动挖掘思维的潜能去探究解题的思路.
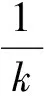
由二次方程(1)有2个不相等的实根,得
根据P1P2的中点N(x0,y0)既在直线P1P2上,又在直线l上,可得
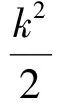
代入式(2)解得,-2 思路2利用直线的参数方程.将过P1P2中点N的直线参数方程代入抛物线方程,得到关于参变量t的二次方程.点P1,P2分布在点N的2侧,只需t1+t2=0且t1t2<0,由此可得关于k的不等式. 笔者在设计问题时,只是提供了学生较宽广的思维空间,但在此空间里,学生研究问题所绽放出的新颖的想法使笔者始料不及.在研究学习中,让学生感到数学思想方法来得自然,来得真切.过程的开放也许会影响课时进度和教学任务,但这并不影响学生的整体发展,有助于学生在课堂教学中的有效学习. 建构主义指出:数学学习并非是一个被动的接受过程,而是一个主动的建构过程,也就是说数学知识必须基于个人对经验的操作、交流,通过反省来主动建构.通过对例题的再创造,启发学生积极思维,引导学生自己探索、发现新知识点,使学生在探究中感受乐趣、体验成功,驱动学生探究的热情,从而有效地让学生领悟数学思想和数学方法. 教材上的例题具有典型性,但缺乏开放性、灵活性.因此通过改造课本上的例题,重新设计开放性数学问题,使其更具有系统性、开放性. 变式4在变式3中,如果把“椭圆”改为“双曲线”或者把“2个焦点”改为“长轴两端点”或“焦点弦”,那么充要条件又是怎样呢? 多设计开放性数学问题,可以促进学生的开放性学习,有利于培养学生的创新能力.改造课本上的例题首先要找准探究的切入点,放低身段,狠抓落实,让研究性学习成为提高复习效率的推手,问题研究的支点也是知识的生长点.“题不在多,经典就行”,此话道出了例题的重要性,如何使例题教学的功能最大化,是首先要考虑的问题.在教学中,设计有效问题探究的支点时,还要注意教学实际的时效性和量力性,再精彩的题目如果学生“跳一跳”还够不到,那么其结果将只能是“我本将心照明月,奈何明月照沟渠”. 一个人在融洽的气氛中的思维是最活跃的,学习的效果也是最佳的.教学从本质上说是一种沟通与合作的活动,因此可以被理解为是一种语言性沟通或语言性活动,其中“对话”是教学活动的重要特点.因此在教学过程中,建立生生之间、师生之间的交流平台,使教师和学生交互作用形成学习共同体,人人参与,平等对话,真诚沟通,彼此信赖,发展合作精神,激发勇气,共享经验知识,促进每一个学生的个性化学习. 例如,在等比数列前n项和求和公式的推导过程中,教师写出 直接引出错位相减法求和,学生就一定会问,你是怎么想到的呢?基于此,笔者在写出式(3)后,提出问题:“同学们可有什么想法?”结果几乎全班同学一致认为应该提取a1,将式(3)变形为 Sn=a1(1+q+q2+…+qn-1). “接着呢?”笔者继续提问,这时学生沉默了,过一会儿有学生轻轻地说:“老师,能不能对式(4)括号中的q+q2+…+qn-1再提取q?”笔者就顺着他的思路将式(4)继续变形为 接下去学生就活跃起来了,想法也多了起来.在大家的努力下,产生了如下解法: 设1+q+q2+…+qn-1=Tn,则 1+q+…+qn-2=Tn-1(n≥2且n∈N*), 从而 Tn=1+qTn-1. 当q=1时,Tn-Tn-1=1,于是{Tn}是以T1=1为首项,1为公差的等差数列,得 Tn=1+1·(n-1)=n, 从而 Sn=a1n(q=1). 即 因此 以上方法虽然复杂,但却是学生智慧的结晶. 在课堂教学中,教师应当以真情来打通走进学生心灵的隧道,努力为学生缔造宽松、自由的数学学习环境,营造平等、和谐的课堂气氛,与学生建立民主、平等的师生关系,把课堂成为师生互动的“情感场”.著名教育家第斯多顿曾经这样说“教育的艺术不在于传授本领,而在于激励、唤醒、鼓舞”.因此在课堂教学上,教师要更多地唤醒学生的智慧,激励学生的斗志,鼓励学生尝试探索,最大限度地让学生在活动中学习,在主动中发展,在合作中增加,在探究中创新,逐渐步入“教”与“学”互促互动、相得益彰的良性循环轨道.如果师生关系不融洽,甚至出现敌对的情绪,那么即使教学过程设计得再好,学生也很难参与进来,一切都是徒劳的. 数学学习方式多种多样,主要有主体学习、研究性学习、开放性学习、个性化学习,还有经验性学习、合作性学习等等.它根植于课堂,得益于教师精心培育,成熟于学生的不断实践,对提高数学课堂教学的有效性有着不可低估的作用.作为教师,应在课堂教学的主阵地上致力于培养学生掌握适合自己的数学学习方式,促进自身课堂的有效学习. [1] 吴庆麟.教育心理学——献给教师的书[M].上海:华东师范大学出版社,2003.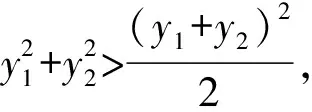
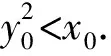
2 改造教材例题,促进学生的开放性学习


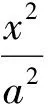
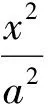
3 建立平等交流的平台,促进学生的个性化学习