Brandt半群的半自同构

杨浩波

(杭州师范大学 钱江学院,浙江 杭州 310012)

0 引 言

设S是一个半群,一个双射φ:S→S叫做半群S上的一个半自同构[1],若对任意的a,b∈S有(aba)φ=(a)φ·(b)φ·(a)φ.关于半自同构的综述见文[1].特别指出的是,在文[1]中,非空集合X上的对称逆半群IX的一个逆子半群S被称为覆盖X,若S包含IX的所有常值幂等元和空变换,并得到下面结果.

定理1([1],Th.4)设S为对称逆半群IX的覆盖X的2-传递逆子半群,则S的每个半自同构或是自同构,或是反自同构.

若令K为IX的所有常值变换和空变换组成的集合,则K为IX的最小理想,且K是一个特殊Brandt半群(即完全零单逆半群[2]).笔者注意到,IX的2-传递逆子半群S包含K.在上述定理的证明中,Sullivan[1]将S的半自同构转化到K的半自同构来进行([1],Lemma 2).

在该文中笔者将研究一般Brandt半群上的半自同构.

一个Brandt半群由下面表示[2-3]:设G为一个群,I为一个非空集,0是一个不在卡尔集I×G×I里的一个元素(叫零元).在集合B(G,I)=(I×G×I)∪{0}上定义二元运算为:对(i,g,j),(s,h,t)∈I×G×I,

则B(G,I)是一个Brandt半群;反之任一个Brandt半群被如此构作.

1 主要结果与证明

对Brandt半群B(G,I)，需要下述术语.令

AG={双射χ:G→G|∀a,b∈G,(aba)χ=aχ·(b-1χ)-1·aχ}.

有

引理1(1)AG非空;

证明(1)群G的恒等自同构是AG的元素,AG非空.(2)和(3)可直接验证.

另需要

FI={f:I×I→I|映射α:I×I→I×I,(i,j)α=(f(i,j),f(j,i))为双射}.

FI同样也非空，这是因为投影η:I×I→I定义为

η(i,j)=i,(∀(i,j)∈I×I)

是FI的一个元素.

文章的主要结果是：

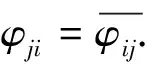
(i,g,j)φ=(f(i,j),gφij,f(j,i))，
0φ=0.

则φ是B(G,I)的一个半自同构；反之，B(G,I)上的任一个半自同构被如此构作.

证明现证φ是双射.由假设f,φij的定义知，φ是一个映射.下证φ是一个满射.任意取(k,b,l)∈B(G,I)，由f的定义，存在i,j∈I使f(i,j)=k,f(j,i)=l.再由φij的定义知，存在a∈G使aφij=b.进而(i,a,j)φ=(k,b,l).故φ是一个满射.

下证φ是单射.任取(i,a,j),(k,b,l)∈B(G,I)，假定(i,a,j)φ=(k,b,l)φ，则有：

(f(i,j),aφij,f(j,i))=(f(k,l),bφkl,f(l,k))，

这表明f(i,j)=f(k,l),f(j,i)=f(l,k),aφij=bφkl，进而由f为FI的元知：(i,j)=(k,l)，从而aφij=bφij，注意到φij∈AG并知：a=b，故(i,a,j)=(k,b,l)，因此φ是单射.

现证：任取(i1,g1,j1),(i2,g2,j2)∈B(G,I)有

[(i1,g1,j1)(i2,g2,j2)(i1,g1,j1)]φ=(i1,g1,j1)φ·(i2,g2,j2)φ·(i1,g1,j1)φ，

(*)

分以下两种情况来讨论：

情况1(j1,i1)≠(i2,j2).此时有(i1,g1,j1)(i2,g2,j2)(i1,g1,j1)=0.又由f的定义知，

(f(j1,i1),f(i1,j1))≠(f(i2,j2),f(j2,i2)).从而

[(i1,g1,j1)(i2,g2,j2)(i1,g1,j1)]φ=0φ=0，且

(i1,g1,j1)φ·(i2,g2,j2)φ·(i1,g1,j1)φ=

(f(i1,j1),g1φi1j1,f(j1,i1))(f(i2,j2),g2φi2j2,f(j2,i2))(f(i1,j1),gφi1j1,f(j1,i1))=0，

这表明(*)式成立.

情况2j1=i2且j2=i1.此时先有

[(i1,g1,j1)(i2,g2,j2)(i1,g1,j1)]φ=(i1,g1g2g1,j1)φ=(f(i1,j1),(g1g2g1)φi1j1,f(j1,i1)),

同时注意到f(j1,i1)=f(i2,j2)，f(j2,i2)=f(i1,j1)有：

(i1,g1,j1)φ·(i2,g2,j2)φ·(i1,g1,j1)φ=

(f(i1,j1),g1φi1j1,f(j1,i1)(f(i2,j2),g2φi2j2,f(j2,i2))(f(i1,j1),g1φi1j1,f(j1,i1))=

f(i1,j1),g1φi1j1g2φj1i1g1φi1j1,f(j1,i1))=(f(i1,j1),(g1g2g1)φi1j1,f(j1,i1)).

故这表明(*)式成立.

综上所述，映射φ是B(G,I)的一个半自同构.

为证定理2的反方面,笔者从下面若干引理来进行.

引理2设φ是含零半群S的一个半自同构，则0φ=0.

证明设a∈S使aφ=0，则由φ是半自同构知：

0φ=(0a0)φ=0φ·aφ·0φ=0φ·0·0φ=0.

引理3设φ是逆半群S的一个半自同构，则对任意a∈S,(aφ)-1=a-1φ.

证明由aφ=(aa-1a)φ=aφ·(a-1)φ·aφ和a-1φ=(a-1aa-1)φ=a-1φ·(a)φ·a-1φ知(aφ)-1=a-1φ.

在下面引理4至引理6中都假定e是群G的单位元,设φ是Brandt半群B(G,I)上的任一个半自同构.任取(i,g,j)∈B(G,I)，并令

(i,g,j)φ=(fg(i,j),gφij,hg(i,j)),

(1)

其中fg(i,j),hg(i,j)∈I;gφij∈G.于是有：

引理4fg(i,j),hg(i,j)与g无关.

证明由引理2知(i,g,j)φ≠0，进一步有：

0≠(i,g,j)φ=[(i,e,j)(j,g,i)(i,e,j)]φ=(i,e,j)φ·(j,g,i)φ·(i,e,j)φ=

(fe(i,j),eφij,he(i,j))(fg(j,i),gφji,hg(j,i))(fe(i,j),eφij,he(i,j))=

(fe(i,j),eφijgφjieφij,he(i,j)).

又由已知有：(i,g,j)φ=(fg(i,j),gφij,hg(i,j))，故有：

fg(i,j)=fe(i,j),hg(i,j)=he(i,j).

这表明fg(i,j),hg(i,j)与g无关.证完.

由引理4立即知：任取(i,g,j)∈B(G,I)，都有：

(i,g,j)φ=(f(i,j),gφij,h(i,j)).

(2)

引理5在式(2)中，任意(i,j)∈I×I，有h(i,j)=f(j,i).

证明任取非零元(i,g,j)∈B(G,I)，由φ是半自同构知：

0≠(i,g,j)φ=[(i,e,j)(j,g,i)(i,e,j)]φ=(i,e,j)φ(j,g,i)φ(i,e,j)φ=

(f(i,j),eφij,h(i,j))(f(j,i),gφji,h(j,i))(f(i,j),eφij,h(i,j))

故必有h(i,j)=f(j,i).证完.

由引理5立即知：任取(i,g,j)∈B(G,I)，有：

(i,g,j)φ=(f(i,j),gφij,f(j,i)).

(3)

下面两引理研究式(3)中映射f:I×I→I和φij:G→G的性质.

引理6在式(3)中，有

(a)f:I×I→I为映射.

(b) 对任意k,l∈I，方程f(i,j)=k，f(j,i)=l有惟一解i,j∈I；

从而f∈FI.

证明明显(a)成立;下证(b).任意给定k,l∈I，g′∈G，由φ为双射知，存在i,j∈I,g∈G使(i,g,j)φ=(k,g′,l)，进而由式(3)有f(i,j)=k，f(j,i)=l.

假设存在另一组m,n∈I，使得

f(m,n)=k,f(n,m)=l.

则由式(3)有：

(i,e,j)φ=(f(i,j),eφij,f(j,i))=(k,eφij,l)，
(n,e,m)φ=(f(n,m),eφnm,f(m,n)=(l,eφnm,k)，

由φ是半自同构进一步有：

0≠(k,eφijeφnmeφij,l)=(k,eφij,l)(l,eφnm,k)(k,eφij,l)=

(i,e,j)φ·(n,e,m)φ·(i,e,j)φ=[(i,e,j)(n,e,m)(i,e,j)]φ.

故由引理2,(i,e,j)(n,e,m)(i,e,j)≠0,从而有m=i,n=j.(b)得证.

引理7在式(3)中，有

(a) 映射φij:G→G为双射；

(b) 任取a,b∈G,i,j∈I有

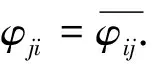
从而φij∈AG.

证明先证(a).取定g′∈G,因φ为满射和(f(i,j),g′,f(j,i))∈B(G,I)，故有g∈G使(i,g,j)φ=(f(i,j),g′,f(j,i)),从而gφij=g′.故φij:G→G为满射.

下证φij是单射.任取g,h∈G，若gφij=hφij，则有：

(f(i,j),gφij,f(j,i))=(f(i,j),hφij,f(j,i))，

即(i,g,j)φ=(i,h,j)φ，由φ是双射知：(i,g,j)=(i,h,j)，故g=h.因此φij是单射.(a)得证.

现证(b).任取i,j∈I，a,b∈G有

(f(i,j),(aba)φij,f(j,i))=(i,aba,j)φ=[(i,a,j)(j,b,i)(i,a,j)]φ=

(i,a,j)φ(j,b,i)φ(i,a,j)φ=

(f(i,j),aφij,f(j,i))(f(j,i),bφji,f(i,j))(f(i,j),aφij,f(j,i)))=

(f(i,j),aφijbφjiaφij,f(j,i)).

故(aba)φij=aφijbφjiaφij.

任取i,j∈I,a∈G,据引理3有[(j,a,i)φ]-1=(j,a,i)-1φ,从而

(f(i,j),(aφji)-1,f(j,i))=(f(i,j),a-1φij,f(j,i)),

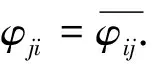
到此,定理2得证.

[1] Sullivan R P. Semi-automorphisms of transformation semigroups[J]. Czechoslovak Mathematical Journal,1983,33:548-554.

[2] Howie J M. An Introduction to Semigroup Theory[M]. London: Academic Press,1976:1-269.

[3] Lawson M V. Inverse Semigroups The Theory of Partial Symmetries[M]. Singapore: World Scientific,1998.