科学理论可检验性问题的新理解——兼与林定夷教授商榷

刘 洋， 万小龙

(华中科技大学 人文学院， 湖北 武汉 430074)

林定夷教授在2007年和2008年公开发表了五篇关于科学理论的检验及科学与非科学划界等问题的重要文章。在文章中， 林先生以其特有的明晰、 严密对已往关于科学理论的诸多问题进行了精致的总结、 分析和批判， 并且给出了自己关于科学理论检验的结构和逻辑的创新观点， 让我们又一次领略了“林问题”的学术风采。我们在学习林先生大作的过程中， 受益非浅， 但也发现一些问题想要与林先生商榷。

一、 关于“科学理论接受经验检验的逻辑模型”

林定夷教授曾在《论科学理论的检验结构和检验逻辑》一文中用了大量的篇幅来批评和讨论波普尔证伪主义模型， 内容十分的详实、 丰富。但我们有一些不同的看法。

首先， 林先生认为波普尔的证伪模型具有不完善性， 因此构建了自己的检验模型， 认为科学实践中不单是从受检理论单独导出检验蕴涵， 而是 “要从受检理论T、 一组初始条件和边界条件的集合C以及相关的辅助假说集H的合取中， 才能导出检验蕴涵P。”[1]我们要提出的是， 既然林先生考虑的是“一般结构与逻辑”， 而C和H的形式地位是相同的， 就没有必要把C和H两种在逻辑上平权的因素分别讨论， 而既增加了逻辑形式的复杂性也增加了文章的篇幅。况且仅列出C和H也并不能穷尽影响检验结果的因素。

其次， 林先生认为， 他本人的模型不具有奎因的整体论模型的混沌性 ， 他说“我们的模型所表述的思想与美国哲学家W. 蒯因(Willard Van Orman Quine 1908-)所表述的我只能称之为‘混沌的整体主义’的观念却有着原则的不同”。[1]关于这点我们也不能十分认同， 因为理论虽然包括了各种因素以决定影响检验结果， 但整体论可能指各种因素的整体影响并不总是等于各种因素分别影响的逻辑复合。

第三， 是最重要的问题， 林先生在讨论“科学理论接受经验检验的一般结构与逻辑”时首先研究一种最简化的抽象模型， 他说“一个受检理论(或原理)T能直接导出某种检验蕴涵 P， 并且假定我们通过实验或观察所获得的观察陈述S0是可靠的， 而这个观察陈述S0将能证实或否证理论所导出的那个检验蕴涵P0简言之， 对这种模型可作如下简要的描述， 即：

(1)T→P

(2)S0可靠

以此为基础来讨论科学理论的检验问题。”[1]

并且把上述模型看作是波普尔关于科学理论检验的证伪主义方法论的一个逻辑重构， 并且说“由此就可以根据两个逻辑重言式来讨论科学理论的检验问题 ， 即：

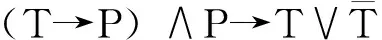
(I)

我们认为， 林先生在这里的确把波普尔的思想明晰化和严密化了， 体现出波普尔的“作为普遍陈述的科学原理或理论是只可被证伪， 不可被证实的”基本思想。

不过， 在与实际科学史相比较之后， 林先生又说到“我们就不能认为可以简单地从受检理论中直接导出检验蕴涵了； 而是必须认为， 我们往往要从受检理论、 一组初始条件和边界条件的集合以及其他辅助性假说的合取中， 才能导出这种可与观察经验相比较的检验蕴涵， 而且通过实验和观察活动所获得的观察陈述也不能无条件地保证一定是可靠的， 而是可错的。”[1]并且构建出一种比较接近实际的科学理论的简要但却完整的检验模型的描述：

“ (1) T∧C∧H →P

(2) S0可错

其中， T表示受检理论 ， C表示一组初始条件和边界条件的集合， H表示其他相关辅助假说的集合 ， P表示检验蕴涵， S0表示观察陈述。”[1]

而相应的“涉及科学理论之检验的相应的逻辑公式也应当改写为：

(1) ( T∧C∧H →P) ∧P

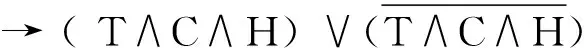
我们无法认同林先生后面的模型： 因为他的模型描述(B)不比(A)更明晰， 而他的逻辑公式II比逻辑公式I更不接近科学实践的实际。

科学家在对一个科学理论进行经验检验时， 的确必须使用初始条件和边界条件， 并且常常还要使用其他相关辅助假说等手段。但是， 他们从来不是“从受检理论、 一组初始条件和边界条件的集合以及其他辅助性假说的合取中， 导出这种可与观察经验相比较的检验蕴涵”(C)， 更不是“才能导出检验蕴涵”(C#)！持有观点(C)或增强版的(C#)的科学家实际是对他们自己的科学实践工作的一个业余科学哲学表述， 而持有观点(C)或(C#)的科学哲学家很可能从这里开始对科学理论的可检验性问题的讨论误入歧途！

我们认为一个合适的模型应该具有如下的过程： 全称陈述的科学理论导出一个单称科学陈述， 这一单称陈述接着又导出一个受检蕴含， 最后将这一受检蕴含与初始条件、 边界条件的集合以及辅助性假说等因素合取导出可被经验检测的检验结果。我们称之为模型(逻辑公式)(III)。

二、 模型(III)的例证

下面我们运用这个新的检验逻辑来分析林先生对他的“简要但却完整的检验模型”的逻辑公式在具体科学史中的运用。

(一)怀疑实验(或观察)结果的正确性

林先生用“当考夫曼于1906年宣布， 他用高速电子实验‘证明’在他的实验中‘量度的结果同洛伦兹一爱因斯坦假定不相容’”[1]这个科学实例来说明当理论的预计与实验结果相矛盾时， 不一定说明理论错了， 而可以怀疑实验(或观察)结果的正确性， 这个例子举的很恰当。但它正好说明了考夫曼实验验证的不是从相对论理论与其他“初始条件和边界条件的集合以及其他辅助性假说的合取”中导出的检验蕴涵， 而是从相对论理论中导出的单称陈述“考夫曼1906年高速电子实验中的电子符合洛伦兹一爱因斯坦变换”与实验误差的合取。

(二)怀疑初始条件和边界条件

林先生用“天王星的实测轨道与根据牛顿理论所计算的轨道不符”[1]， 导致伽勒于1846年终于发现了海王星作为例子来说明当理论预见与实际观察不符时， 可能是初始条件和边界条件的问题而不一定是理论本身的问题。不过， 这个例子正好形象的说明了当时的科学家不是在用经验检验牛顿理论与“初始条件和边界条件”合取推出的逻辑后承， 而是检验的从牛顿理论单独推出的逻辑后承“天王星与太阳之间有符合万有引力定理的引力”与初始条件和边界条件“唯一要记入的就是这个引力”这两者的合取。

(三)辅助性假说

林先生根据“当能量守恒定律与当年的B衰变实验的结果不符时， 泡利实际上就是通过设定一个辅助性的假说 (中微子假说)而维护了能量守恒定律”，[1]这个科学史实说明辅助性假说能够帮助理论逃脱被证伪。但例子正好说明了： 虽然能量守恒定律逃脱被证伪是因为从能量守恒定律中推出的单称陈述“在那次B衰变实验中能量守恒”与“在那次B衰变中不存在中微子作用”的合取被证伪了。但如果“在那次B衰变中存在中微子的作用”这个辅助性假设是真的， 那么“在那次B衰变实验中能量守恒”这个陈述就没有被证伪， 那么， 能量守恒定律就没有被证伪。

(四)修改受检理论

林先生认为， “当理论上所导出的检验蕴涵与实验观察结果不相容时， 我们也可以指责受检理论。”但是， 他又认为 “科学家们就采取行动， 抛弃或修改这个理论。” “但是， 我们指责受检理论因此‘被证伪’， 那是始终不可能有充分的理由的。因为按照我们的模型， 在这种情况下， 只有预先断言实验观察结果 、 所设定的初始条件集合和所引进的其他辅助假说都准确无误， 才有充分的理由断言： 一定是这个受检理论错了， 即它被证伪了。然而， 这是不可能的。”[1]

照林先生的模型， 不但“当检验蕴涵与实验观察结果不相容时， 指责受检理论没有必然的可靠性”， 因为实验观察有易谬性； 而且即使“检验蕴涵被可靠地验证为假时， 指责受检理论仍然没有必然的可靠性”， 因为检验蕴涵是被受检理论与其他陈述合取而推出的。因此， 通过检验蕴涵来验证理论， 既在经验上不可靠， 又在逻辑上不可靠； 或者说， 在科学理论的检验逻辑上， 检验蕴涵的逻辑程序前后都不可靠。

而在我们的逻辑程序中， 如果“当待检验蕴涵与实验观察结果不相容时， 指责受检理论没有必然的可靠性”； 但如果“待检验蕴涵被可靠地验证为假时， 指责受检理论为假就有必然的可靠性”， 因为待检验蕴涵是被受检理论单独推出的。

三、 模型(III)的优势

我们的模型(III)正是吸收了林先生的细致分析的素材， 并且继承了波普尔逻辑程式的基本内容而建立的。下面具体分析模型(III)的优势。

(一)语言的明晰性

模型(III)的逻辑程式由两部分组成。

第一部分与林定夷教授明晰地指出的波普尔的逻辑程式在命题形式上相同：

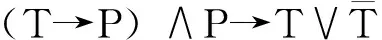
但进一步明晰波普尔的思想。包括： 这里的P作为全称性科学理论陈述T的逻辑后承必须是一个单称陈述； P作为科学理论的可检验后承的可检验性不是仅指“它原则上可以与观察结果比较”而是指“它原则上可以直接与观察结果比较或者通过与初始条件和边界条件的集合以及其他辅助性假说的合取而间接与观察结果比较”。

第二部分， 与林先生的新模型的逻辑程式在逻辑形式上具有可类比处， 但其中的受检理论T换成受检蕴涵P， 而其中的受检蕴涵P换成可观察结果的预言S， C表示一组初始条件和边界条件的集合， H表示其他相关辅助假说的集合 ， P表示检验蕴涵， S。表示观察陈述， 并且他们都是单称陈述：

((P∧C∧H)≡S)∧S→P∧C∧H

在其中， 我们可以十分明晰的看到： 所谓的全称科学陈述的证实与证伪的不对称性， 在这个新程式的第一部分； 而所谓的经验可检验性在这个程式的第二部分。

(二)推理的严密性

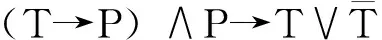
(三)经验的可靠性

科学家在实践中完全可以先单独从一个全称性理论陈述推出一个待检验的单称陈述， 然后再考虑这个单称陈述的检验问题。分析下面三种情况：

1. 关于某一类个体的全称命题

如“所有的金属都是导电的” ( 1)可以规范地写为： “对于任意一个个体来说， 如果它是金属， 那么它是导电的”。 设F为金属， G为导电的。

公式化后显然有： ∀x(Fx →Gx)→(Fa →Ga)。(Fa →Ga)可自然化为： “如果a这个个体它是金属， 那么它是导电的”(1-1)。注意(1-1)并不等价为“a这个金属是导电的” (1-2)。更进一步说， 从(1)并不能单独地推出(1-2)， 但能够单独地推出(1-1)。现在要证伪(Fa →Ga)也就是要证伪(﹁ Fa ∨Ga)， 即要证实(Fa ∧﹁ Ga)。

结论： 如果证实a是金属并且证伪a导电， 那么就必然可以证伪“所有的金属都是导电的”。

2. 关于一切个体的全称命题

“任意个体都有能量” (2)， 设个体X， 有能量H， 那么(2)可公式化为一个简单命题： ∀x Hx显然有， ∀x Hx→Ha。Ha可自然化为： “a这个个体是有能量的”(2-1)。 只要证伪了(2-1)就必定证伪(2)。

3. 关于全称存在命题

这是林先生文章中的例子“小儿麻痹症是由某种病毒引起的， 它们都具有这样的形式： ∀x∃y(Ax∧By →Gxy)”[2](3)。其中， A： 小儿麻痹症， B： 病毒， G： 被引起关系。不过更一般地， 我们会把(3)公式化为∀x(Ax→∃y(By∧Gxy))(3-2)。

显然有： ∀∃x(Ax→∃y(By∧Gxy) →(Aa→∃y(By∧Gay)= ﹁ Aa∨∃y(By∧Gay)。要证伪﹁ Aa∨∃y(By∧Gay)即证实Aa∧﹁ ∃y(By∧Gay)。

结论: 只要证实a是小儿麻痹症并且证伪存在一种病毒会引起a这个小儿麻痹症， 那么原理论“小儿麻痹症是由某种病毒引起的”就被证伪了。

显然， 在(1)和(2)中， 全称命题的检验问题已经被简化成单称命题的检验问题。当然， 在(3)中， 全称命题的检验问题只简化成特称命题的检验问题， 而从逻辑上说， 特称命题是否总是不可证伪， 我们将另著文讨论。

(四)逻辑的紧致性

我们的模型具有更高逻辑紧致性的理由是由于在这个模型中待检验蕴涵是直接由理论推导出的， 这其实是将检验对象从全称命题转移到了单称命题， 而单称命题具有比全称命题更强的可检验性。因此， 在我们的模型中待检蕴含能够更容易的被断定是真还是假， 如果是假， 那么原理论也就可被确定为假。但待检蕴含是如何被经验所断定的， 这个问题本身仍是开放的。

四、 科学的划界

科学与非科学的划界问题首先涉及的问题就是“什么是科学？”是理论、 文化还是一种活动？我们必须承认科学是一个令人难以捉摸的事物， 不过至少作为理论的科学， 其内部的定理与陈述还是相当明晰的

在我们的模型中， 证伪与证实的不对称性是十分明显的， 但这种不对称性本身在科学检验的逻辑程式中的两个阶段中也是不对称的。这后一种不对称性表明： 如果你最终想要检验的是一个单称陈述， 那么它的可证实性在原则上要优于可证伪性。如果你最终想要检验的是一个全称陈述， 那么它的可证伪性在原则上有条件地说要优于可证实性。原则上是指在逻辑上说， 可以通过经验检验。有条件地说是指， 在检验的第一阶段， 对单称的相关辅助假说、 初始条件和边界条件(F)的检验相对于对作为受检全称科学陈述的单称的待检蕴涵的检验的独立程度。如果能够独立地检验(F)为真， 那么当由(F)和待检蕴涵合取的对观察结果的预言为假时， 就能够确定地知道待检蕴涵为假， 进而确定地得到待检全称科学陈述为假。

科学定理总是由全称性科学陈述所写成， 因此， 科学定理具有可证伪性。如果从科学定理到科学理论再到科学， 前者依次为后者的划界的必要条件， 那么可证伪性就是科学划界的必要条件， 这个问题仍需要进一步探讨。但至少认为， 科学定理与其他因素共同形成(不一定是组成)了某些整体性的新条件， 这些新条件是科学划界的必要条件或充分条件， 不过这些新条件很可能是在共时和历时中都有实践依赖性和文化依赖性的。

参考文献：

[1] 林定夷. 论科学理论的检验结构与检验逻辑 [J]. 华南理工大学学报(社会科学版)， 2008(2)： 15-19.

[2] 林定夷. 波普尔关于科学与非科学划界的理论 [J]. 华南理工大学学报(社会科学版)， 2007(6)： 21-26.