基于旋量理论的机器人误差建模方法

黄勇刚，杜 力，黄茂林

(1.重庆大学 机械工程学院，重庆400044;2.重庆工商大学 机械工程学院，400067，dulicq@126.com)

精度是衡量机器人性能的一个非常重要的指标，因此机器人误差建模方法研究历来受到重视，主要有矩阵法和矢量法［1］.矩阵法的基础是对齐次变换矩阵的微分，这是目前较常用的建模方法［2］.基于矢量的建模方法主要有摄动法［3］和矢量分析结合螺旋变换法［4］.摄动法基于连杆DH 参数表示，忽略位移和角度摄动的耦合，推导出机器人位姿误差计算公式.矢量分析结合螺旋变换法亦基于D-H 参数表示，用矢量分析方法建立位姿方程，然后对D-H 参数做微分，推导位姿误差与D-H 参数的关系，再采用螺旋矢量简化公式.现代旋量理论在使用矩阵指数以及指数积表示刚体运动的基础上为开链机器人运动学提供了完整的几何描述［5-7］.Moon［8-9］在可重构机床的精度预测和补偿研究中，将传统矩阵微分方法获得的机床模块误差矩阵等效为误差旋量，从而应用现代旋量理论的指数积公式建立了机床的误差模型.谭月胜［10］通过对指数积公式中各旋量参数的微分，得出了一种机械臂末端执行器位姿误差的近似计算公式.

本文直接将机器人各关节旋量误差看成是一种假想广义运动副旋量运动的结果，从而与关节旋量一起建立机器人含误差旋量的运动学指数积公式.定义了机器人工具坐标系的位置误差旋量和姿态误差旋量，并给出其计算公式.应用Matlab编程语言，设计了一套基于旋量的误差分析计算软件包，以SCARA 机器人为例，进行误差仿真分析.使用Adams 软件仿真验证了本文模型和算法的正确性.

1 基于旋量的机器人运动学简介［5］

对如图1 所示具有n 个单自由度运动副的一般开链机器人机构，各关节运动均可看成是旋量，其单位旋量可用Plücker 坐标表示成如下形式［11］:

式中:ω 为旋量轴单位矢量，r 为轴线上任一点的位置矢量，r×ω 为旋量轴对原点的矩，h 为旋量节距.

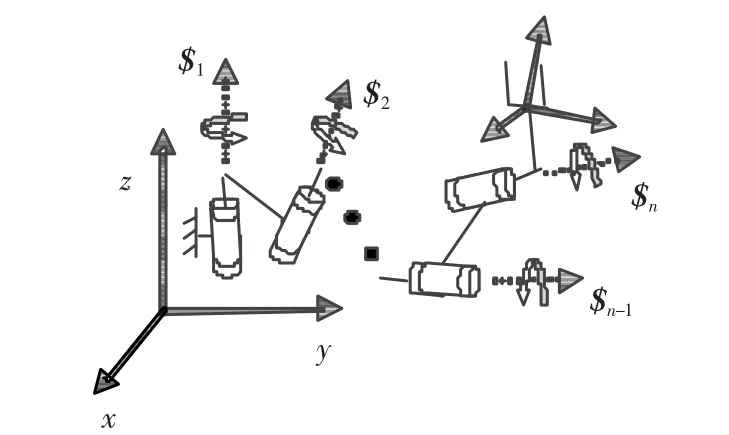
图1 一般开链机器人

设参考位形下工具坐标系在参考系中的位姿为T(0)，此时，各关节单位旋量在参考系中分别表示为:)，则机器人有以下运动学正解指数积公式:

θi为相对参考位形的关节变量，对转动副，是绕轴线转动的角度，按右手定则确定符号，对移动副，则表示移动距离.

式(1)中算子∧运算规则如下:对三维矢量ω，表示叉乘矩阵.即

其矩阵指数可用来表示轴线过坐标原点的旋转变换，有如下的罗德里格斯公式(I 为单位阵)

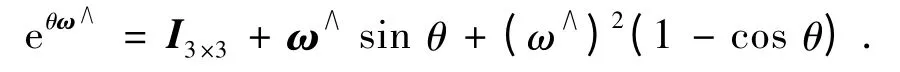
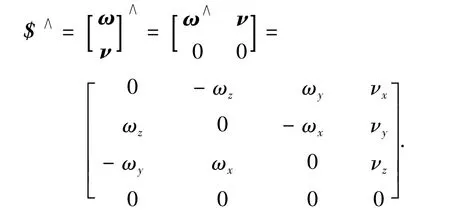
其矩阵指数表示一般刚体变换，计算公式为

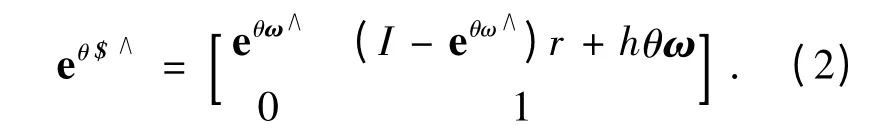
由于旋量是瞬时量，当旋量轴位姿改变时，需要应用伴随变换计算更新其旋量.另外，旋量采用Plücker 坐标，其在不同坐标系中的变换也需要应用伴随变换.

假设A 为固定坐标系，B 坐标系是A 经过旋量θ ＄运动得到的新坐标系，则B 到A 的坐标变换或刚体变换的旋量矩阵指数如式(2)，简记为

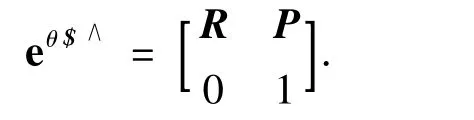
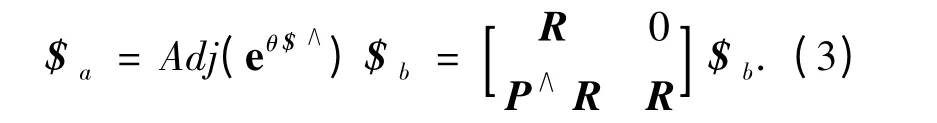
式(1)的指数积采用后运动的旋量矩阵指数左乘法则，即可看成先第n 个关节(最靠近工具端)运动，最后到第1 个关节(连架副)运动.假设关节运动顺序不同，则靠近机架的关节先运动后会改变后面的关节单位旋量坐标，但是通过对所有被影响的关节旋量应用式(4)的伴随变换，结果相同.

2 关节旋量误差的分析和表示

由线几何理论［11］，关节轴线在参考坐标系下可以用其单位矢量和对原点的矩表示，写成Plücker 坐标形式，通过分析各关节轴线的Plücker坐标误差可得到关节单位旋量的误差.

如图2，设机器人某关节轴线理想Plücker 坐标为

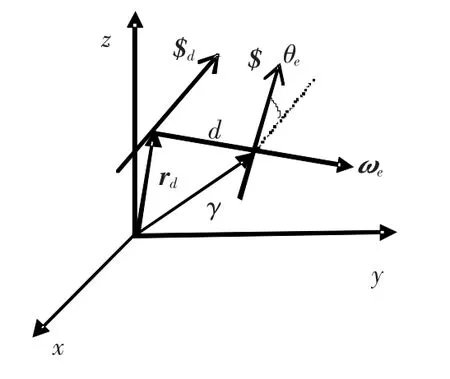
图2 运动副轴线Plücker 会标误差

无其他关节误差影响时，该关节实际Plücker 坐标为

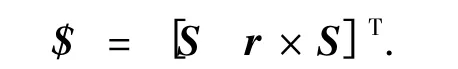
把由理想轴线到实际轴线的Plücker 坐标变化看成是旋量运动的结果，称其为误差旋量，则根据式(3)的伴随变换，有如下关系:

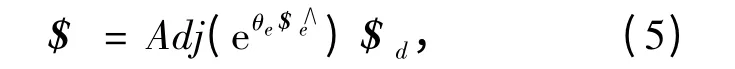
设单位误差旋量表示为

则由式(5)可以求得误差旋量.实际上此误差旋量可以通过观察得到，即:误差旋量是绕理想轴线与实际轴线的公垂线转动角度θe，再沿公垂线移动距离d，转动的角度为两轴线的扭角，移动距离为两轴线的垂直距离.因此:

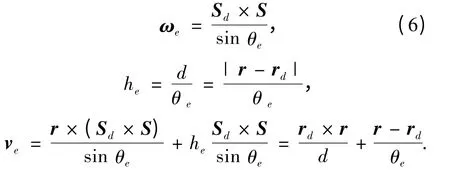
当θe=0 时，即理想轴线与实际轴线平行，误差旋量为纯移动，ωe=0，he=∞，误差旋量退化为

当d=0 时，理想轴线与实际轴线相交，he=0，r=rd，单位误差旋量为

最一般的情形是理想轴线与实际轴线空间相错，d 和θe均不为0，he=d/θe.单位误差旋量为

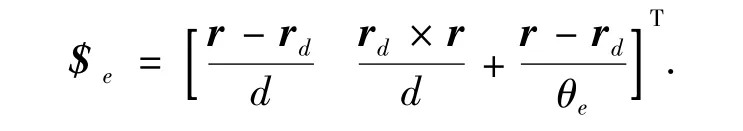
用旋量来表示关节轴线的误差，具有良好的几何直观性，并且不同形式的误差源如位置误差和姿态误差均被统一表示在误差旋量中.

以上分析过程是将误差在固定坐标系下采用旋量表示.假设将理想轴线作为z 轴，将连杆方向作为x 轴建立局部坐标系，则理想轴线在局部坐标系下的Plücker 坐标为

设运动副实际轴线Plücker 坐标为

实际轴线在局部坐标系下的z 方向角即为误差旋量的大小θe，因此

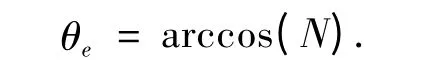
由式(6)可得

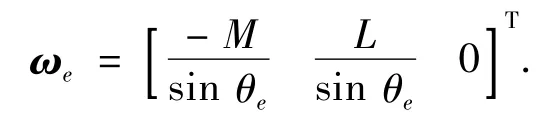
由此，误差旋量的大小θe和误差旋量轴x、y方向余弦分别表示了实际轴线在局部坐标系的姿态误差，从而避免了D-H 表示法难于直接表示绕y 轴线转动误差的不足［2］.误差旋量综合表示了连杆长度误差和形位误差.

虽然误差旋量在局部坐标系下的表示更简单和方便，但还需要根据当前局部坐标系在固定坐标系中的位姿，通过伴随变换转换到固定坐标系.

3 基于旋量的机器人运动学误差模型

3.1 含误差旋量的运动学指数积公式

如图1 所示一般开链机器人，设参考位形时，不考虑其他关节误差的影响，由连架副开始的n个关节轴线在固定坐标系下的误差旋量分别为:.把这些误差旋量看成假想广义运动副，则根据式(2)的指数积公式可直接得到如下含误差旋量的机器人运动学模型:

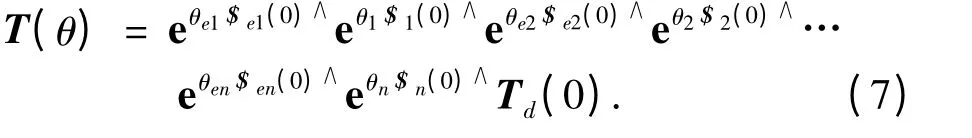
式中:θi为关节变量，是理想关节旋量的大小.而θei是误差旋量的大小，只考虑静态或准静态误差情况下是常量.为机器人关节理想单位旋量.Td(0)为参考位形时工具坐标系的理想位姿.

式(7)的正确性可用关节旋量在误差作用下的伴随变换证明.因为机器人第i 个关节单位旋量Plücker 坐标受到其前面i 个误差旋量的影响，根据伴随变换，各关节实际单位旋量为

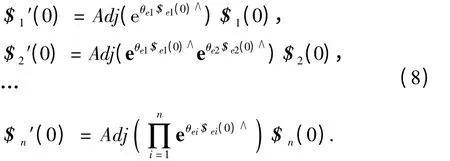
同时，在误差作用下，参考位形时机器人实际位姿为

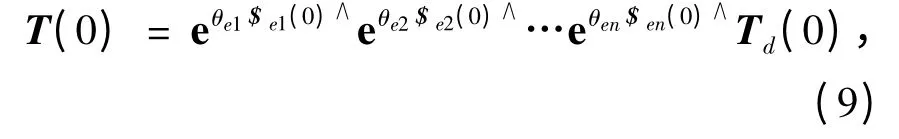
因此，机器人的运动学指数积公式为

根据式(8)和伴随变换式(4)，可得第i 个运动副实际旋量矩阵指数为

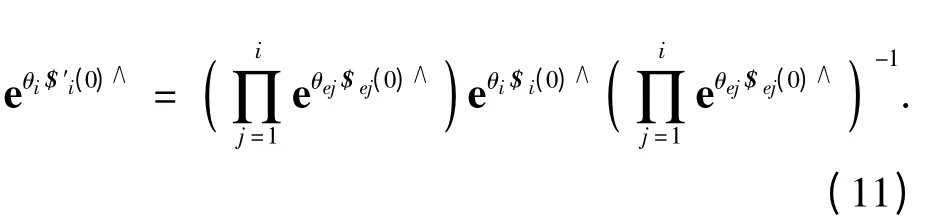
将式(9)和(11)代入式(10)简化后即可得式(7).

式(7)含误差旋量的机器人运动学指数积公式具有明确的几何意义，即:将运动副轴线位姿误差看成是假想广义运动副旋量运动的结果，在静态和准静态下，误差旋量的大小和节距不变，参考位形时将其与理想运动副旋量一起按运动副顺序构成指数积公式，即为机器人含误差运动学方程.因此，只要已知初始位形下各运动副轴线的误差旋量，即可计算出工具坐标系的实际位姿.

3.2 工具坐标系误差的定义

与运动副轴线误差分析类似，同样可以将工具坐标系的位姿误差看成是某一误差旋量运动的结果.然而此时将位置和姿态误差统一表示并不直观，此处将理想工具坐标原点到实际工具坐标原点的位置误差用移动副旋量表示，姿态误差用轴线过理想坐标系原点的转动副旋量表示，如图3.

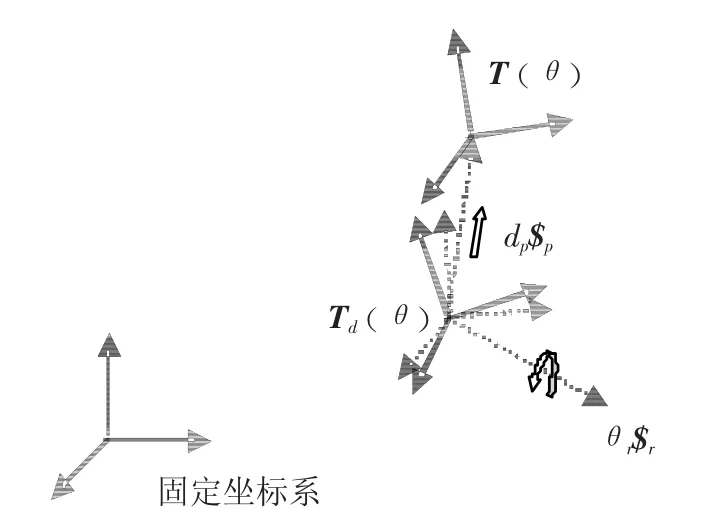
图3 工具坐标系位姿误差的旋量表示

工具坐标系理想位姿如式(1)，其实际位姿如式(7)，假设位置误差和姿态误差旋量均相对固定坐标系表示，则可以看成机器人先通过理想的运动副旋量运动到工具坐标系理想位姿，再经过姿态误差旋量运动到实际姿态，然后经过位置误差旋量运动到实际位置.设位置误差旋量和姿态误差旋量分别为

则如下等式成立:

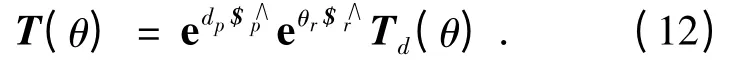
根据前面误差旋量的定义，两种误差旋量在理想工具坐标系下可写成如下形式:

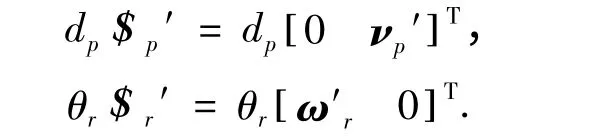
根据伴随变换，两种误差在不同坐标系下的表示有如下关系

因此由式(4)，式(12)可变换为

式(15)表明，在理想工具坐标系下表示的位置和姿态误差旋量矩阵指数积即为传统方法定义的机器人位姿误差矩阵.因此，可以在工具理想坐标系下定义误差旋量为工具坐标系理想位姿到实际位姿的误差，即

由式(16)可以求得位置误差旋量为

后3 个分量分别对应位置误差在工具理想坐标系3 个轴向的分量大小.

可由式(16)求得姿态误差旋量的大小如下

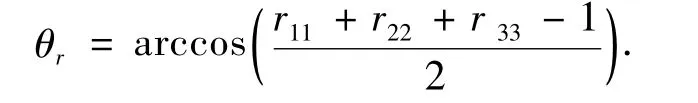
如果θr=0，则只有位置误差没有姿态误差，如果θr不为零，则姿态误差旋量轴在理想工具坐标系下的方向余弦为

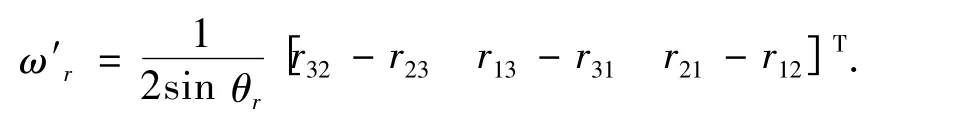
以上两种误差旋量均在理想工作坐标系下表示.根据式(13)和(14)的伴随变换，或是直接根据式(12)，还可以求出两种误差旋量在固定坐标系下的表示.

4 基于Matlab 的误差仿真分析

根据前面基于旋量理论的机器人位姿误差建模过程，在Matlab 下设计了一套通用的旋量计算软件包.利用该软件包，可以对具体的机器人进行误差计算和仿真研究.

以SCARA 机器人为例，该机器人为R//R//C 开链机构，C 副的转动自由度和移动自由度为独立驱动，如图4 所示，两连杆长L1= L2=300 mm.固定坐标系z 轴与第一转动副理想轴线重合，工具坐标系z 轴与C 副轴线重合，x 轴为连杆方向.并记θ1=θ2=θ3=0 时为初始位形，机构无误差参数如下:

假设初始位形时运动副轴线误差参数如下:

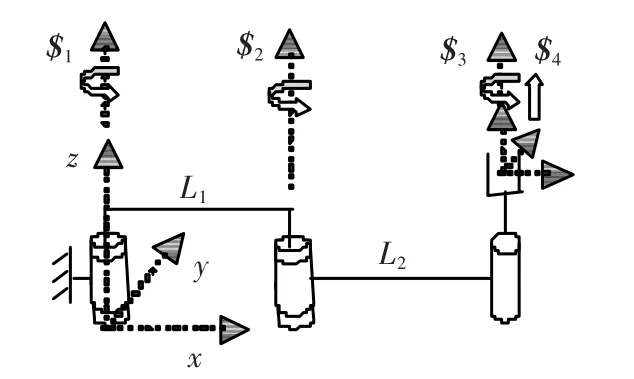
图4 SCARA 机器人机构

设工具坐标系运动轨迹为:从点［400，400，150］开始顺次直线运动到点［-400，400，50］、［-400，-400，150］、［400，-400，50］，最后回到点［400，400，150］，每段直线均为匀速运动1 s 完成，且坐标系姿态保持绕z 轴旋转30°不变.其轨迹曲线如图5 所示，为一空间封闭四边形.

图5 仿真轨迹曲线

根据以上参数和运动轨迹，首先反解出关节变量，由于SCARA 机器人有两个反解构型，此处采用正装配构型，在Matlab 下仿真分析得出的工具坐标系位置误差在固定坐标系下的分量曲线如图6.

对于姿态误差旋量，可以用旋量大小和旋量轴3 个方向余弦曲线表示.为了与ADAMS 中的仿真结果对比，此处将误差旋量转换为理想工具坐标系到实际工具坐标系的3 个罗德里格斯参数表示.转换公式如式(17):

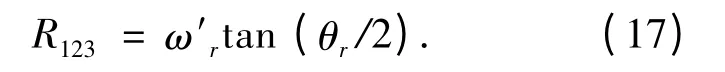
3 个罗德里格斯参数曲线如图7.

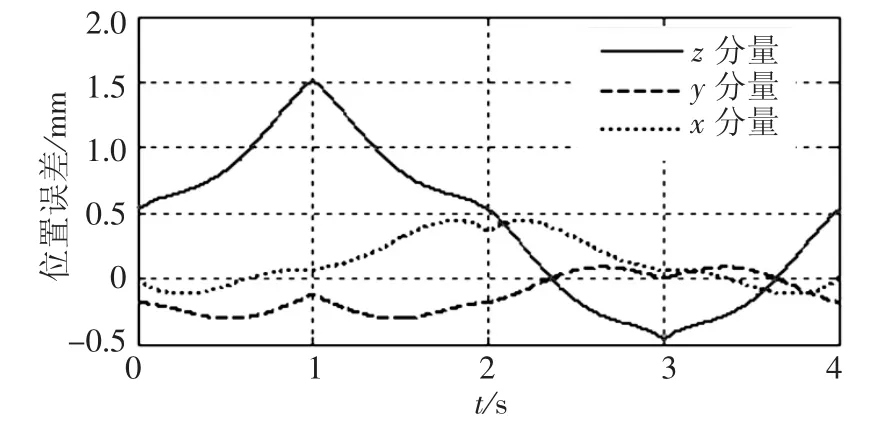
图6 Matlab 仿真位置误差曲线

图7 Matlab 仿真姿态误差罗德里格斯参数曲线

5 仿真结果的ADAMS 验证

为了验证基于旋量的误差建模方法和Matlab软件包算法的正确性，在ADAMS 下对上节的SCARA 机器人按同样的机构参数进行了误差建模仿真分析.

为了在ADAMS 软件下进行误差分析，首先按理想设计参数建立了SCARA 机器人模型，进行反解仿真获得关节驱动参数样条曲线.然后根据误差旋量参数计算获得参考位形下各运动副MARKER 的位姿，从而建立含误差模型，再用理想模型的关节驱动参数样条曲线驱动机构，获得工具坐标系运动.将误差模型的工具坐标系位置曲线与理想模型曲线相减，得到如图8 所示的位置误差在固定坐标系下的曲线.测量理想工具坐标系到误差模型工具坐标系的罗德里格斯参数，得到如图9 所示的曲线.

图8 Adams 仿真位置误差曲线

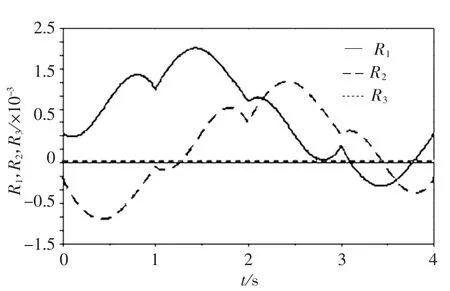
图9 Adams 仿真姿态误差罗德里格斯参数曲线

比较图6 和图8 以及图7 和图9，可以看出，基于旋量的误差建模仿真与用Adams 建模仿真结果相同，证明了该方法的正确性.

6 结 论

1)将运动副轴线的位姿误差看成是旋量运动的结果，从而应用旋量的矩阵指数以及指数积建立机器人误差模型，具有明显的几何直观性.

2)将工具坐标系的位置误差和姿态误差分别用移动副旋量和转动副旋量表示，并给出了其在固定坐标系和在理想工具坐标系中的计算公式.用旋量的大小和旋量螺旋轴的方向表示误差，几何意义明确.

3)在Matlab 下设计了旋量计算软件包，并以SCARA 机器人为例，在给定运动副轴线误差情况下进行了仿真计算，并在Adams 下按相同参数进行了对比仿真.证明了该误差建模方法的正确性.

4)本文的误差建模方法具有良好的几何直观性，可以从整体上描述机器人的实际运动.不需要旋量在不同位形下的变换计算，简化了分析过程，计算量减少了约2/3.与传统矩阵微分方法比较，消除了误差矩阵非齐次性引起的计算误差.

5)该方法不仅可用于静态和准静态误差分析，如果考虑误差旋量的大小和节距随机构运动过程变化，还可用于动态误差的分析.

［1］阎华，刘桂雄，郑时雄.机器人位姿误差建模方法综述［J］.机床与液压，2000(1):3-5.

［2］NIKU S B.机器人学导论——分析、系统及应用［M］.孙富春，朱纪洪，刘国栋，等译.北京:电子工业出版社，2004.

［3］SUGIMOTO K，OKADA T.Compensation of positioning errors caused by geometric deviation in robot system［C］//Robotics Research:The second international Symposium.Cambridge:MIT Press，1985:231-236.

［4］徐卫良.机器人机构误差建模的摄动法［J］.机器人，1989，3(6):39-44.

［5］理查德·摩雷，李泽湘，夏恩卡·萨思特里.机器人操作的数学导论［M］.徐卫良，钱瑞明，译.北京:机械工业出版社，1998:11-44.

［6］张付祥，付宜利，王树国.闭链级联式机器人基于旋量理论的运动学分析方法［J］.机械工程学报，2006，42(4):112-117.

［7］荆学东，浦耿强，王成焘.应用基于运动螺旋的机器人正解映射求解FANUC 机器人的逆运动学问题［J］.机械科学与技术，2003，22(3):402-405.

［8］MOON S K，MOON Y M，SCREW S K.Theory Based Metrology for Design and Error Compensation of Machine Tools［C］//Proceedings of DETC’01.Pittsburgh，Pennsylvania:［s.n.］，2001.

［9］MOON S K.Error prediction and compensation of reconfigurable machine tool using screw kinematics［D］.［S.l.］:The university of Mchigan，2002.

［10］谭月胜，孙汉旭，贾庆轩，等.旋量理论在机械臂末端执行器运动精度分析中的应用研究［J］.机械科学与技术，2006，25(5):534-538.

［11］黄真，赵永生，赵铁石.高等空间机构学［M］.北京:高等教育出版社，2006:2-18.