采用AKF 神经网络的直扩系统抗干扰技术

徐定杰，赵丕杰

(哈尔滨工程大学 自动化学院，哈尔滨150001，zhaopijie407@163.com)

扩频系统除了具有保密性强、可实现码分多址和高精度测量的优点外其抗干扰能力也很强，因此被广泛应用于无线电及卫星导航中.它通过本地伪码信号与接收信号进行相关得到的扩频增益来抑制干扰信号［1］，具有一定的抗干扰能力，但由于实际信号发射功率限制及作用距离上的衰减，接收到的扩频信号功率非常低，在强干扰条件下，尤其在有意的敌对干扰条件下，干扰强度很容易超出其干扰容限，扩频系统便不能正常工作，这就需要采取其它技术措施增强扩频系统的抗干扰能力.

针对扩频系统时域上的抗窄带干扰技术，人们进行了很多的研究并提出相应的解决方案.文献［2］中给出了一种线性自适应最小均方差(LMS)干扰预测器，这种线性干扰预测器将引入一定误差，因此需要一种非线性干扰预测器.文献［3］中给出了一种非线性自适应近似条件均值(ACM)干扰预测器，它需要已知扩频信号的数量等信息，从而得到扩频信号与环境噪声的联合概率密度分布，然后得出其非线性关系.但在实际环境中，扩频信号的数量是未知的，因此很难得到准确的非线性预测函数.文献［4］和［5］中给出了一种基于递归神经网络(RNN)的非线性干扰预测器，当扩频信号的数量未知时，它能够有效地改善干噪比.但它采用的实时递推学习(RTRL)权值修改算法是基于一阶微分统计量的，因此收敛速度慢，对快时变干扰信号很难准确跟踪.

本文提出了一种基于自适应卡尔曼滤波(AKF)的递归神经网络预测器(RNNP)来消除窄带干扰.它采用一种强有力的非线性工具—全连结神经网络［6-7］来预测干扰信号，然后运用适合于非线性系统的AKF 来反馈修改权值，克服了经典卡尔曼滤波需要精确已知系统的数学模型和噪声统计的缺点和局限性.

文中给出了抗干扰扩频系统的结构框图，并详细描述了RNNP，然后给出了基于渐消记忆指数加权的AKF 权值修改算法的递推公式，最后对基于AKF 学习算法的RNNP 相对于常规抗干扰技术的性能进行了计算机仿真.

1 抗窄带干扰扩频系统

图1 给出了抗窄带干扰扩频系统的简化结构框图.它采用相关前抗干扰模式，主要由RNNP 和一个加法器组成，通过这个干扰消除模块可以对混杂在接收扩频信号中的窄带干扰信号进行估计并消除［8］.

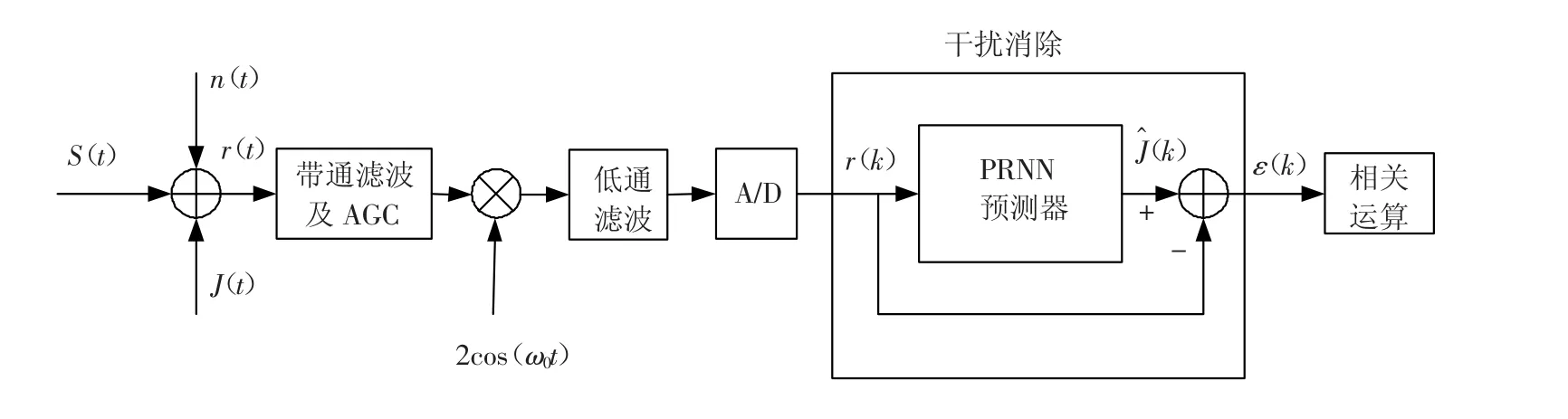
图1 相关前干扰抑制扩频系统结构图

设接收信号可以表示为

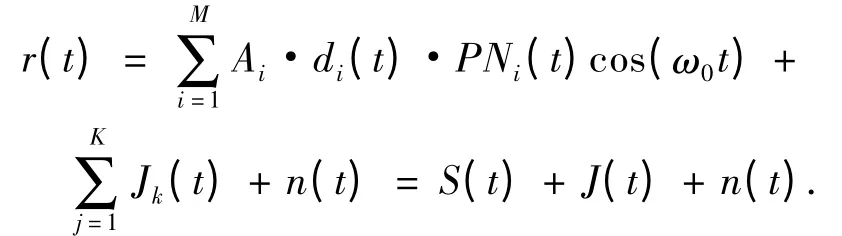
其中Ai为第i 路扩频信号的幅值;di(t)为第i 路二进制数据信息;PNi(t)为第i 路扩频序列，其码片速率远远大于数据信息速率;ω0=2πf0为调制载波角频率;S(t)由M 路扩频信号组成;n(t)为加性高斯白噪声，其均值为零，方差为σ2;干扰信号Jk(t)是指窄带干扰，它的主要来源为接收机附近的雷达及其它射频发射装置发射的强功率信号或敌方针对本扩频系统载波频率而发射的频率在中心频率ω0附近的压迫式干扰，可分为三种形式:音频干扰、自回归(AR)干扰和低速率数字干扰.

接收信号r(t)经过带通滤波器、AGC 固定增益放大、下变频及低通滤波器后，以采样速率fs=1/Ts进行采样，得到的第k 时刻的采样信号为

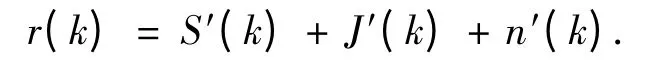
2 基于AKF 的递归神经网络

2.1 递归神经网络预测器

图2 给出了递归神经网络预测器(RNNP)的详细结构，这个模块是一种全连结的神经网络，它由P 个外部输入层神经元、N 个隐层神经元及一个输出层神经元组成.与前向神经网络不同，每个隐层神经元都延迟一个采样周期反馈到输入层，输入层除了P+N 个节点外，还有固定值为+1 的偏值输入.

RNNP 的非线性状态方程及线性观测方程可以表示为

图2 递归神经网络预测器(RNNP)结构框图

其中

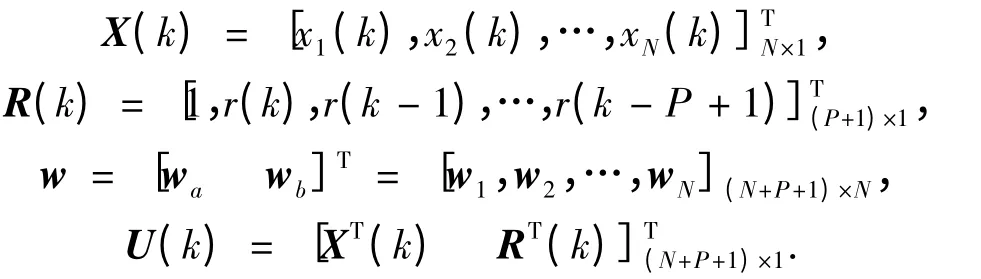
其中:wa为隐层反馈到输入层节点的权值，wb外部输入信号节点的权值，C 为输出层输入输出线性权值系数，X(k)为RNNP 的状态向量，R(k)为外部输入向量，所以总的输入层向量为U(k).输入层的输入输出关系采用直接赋值的方式.

输出层的输入为隐层的输出，输出y(k)为输入的线性组合，即其值为RNNP 预测的干扰信号.

2.2 基于渐消记忆指数加权的AKF 学习算法

根据上面神经网络模型可以得到隐层反馈到输入层权值W(k)的线性状态方程和非线性观测方程为

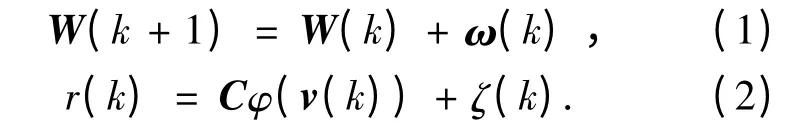
为解决式(2)中非线性观测方程的估值问题，常用的方法是扩展 Kalman 滤波器(EKF)［9-10］，它的缺点和局限性有两点，一是它要求已知状态和观测噪声统计特性，然而实际应用问题中噪声统计特性却常常是近似的、时变的.运用不准确或错误的噪声统计特性设计EKF 将使滤波器性能变坏，甚至使滤波发散.二是EKF的基本原理是将非线性系统线性化，然后用线性化常规Kalman 滤波器解决非线性系统状态估值问题，其中忽略了非线性化引入的模型误差，将导致滤波性能变差.为了解决上述问题，本文采用基于渐消记忆指数加权的AKF 学习算法来修改递归神经网络的权值系数，其原理为:在进行状态滤波的同时，利用观测数据提供的信息，在线估计未知噪声统计特性，构成状态和噪声统计特性估计的两段互耦自适应卡尔曼滤波算法.Sage 和Husa的噪声统计估值器可在线互耦估计状态和噪声统计，算法简单且具有良好的性能，因此被人们广泛应用.它由互耦的常规卡尔曼滤波算法和噪声统计估值器组成.Sage 和Husa 的噪声统计估值器是次优无偏极大后验估值器，适合估计未知的噪声统计，其缺点是不能处理时变噪声统计估计问题，且精度有待于进一步提高.本文引入基于渐消记忆指数加权的改进的Sage 和Husa 噪声估值器，它可处理时变噪声统计估值问题，且计算效率高，能加快收敛速度，提高算法的跟踪性能，使得滤波过程稳定、可靠、精度高.

由于噪声的统计特性未知，将式(2)中的φ在W(k)的预测值)处用泰勒级数展开有

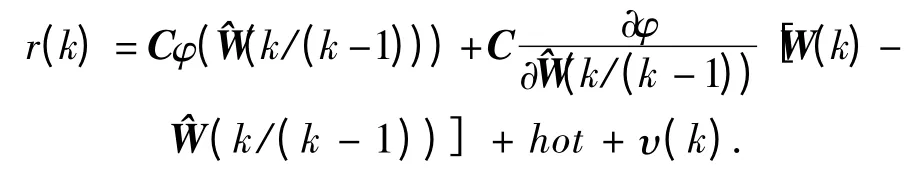
这里引出线性化观测方程

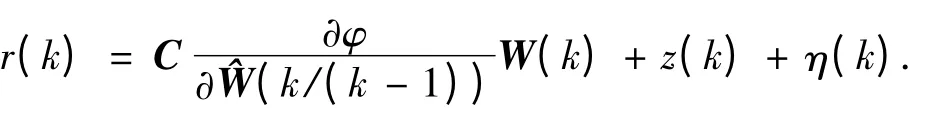
其中

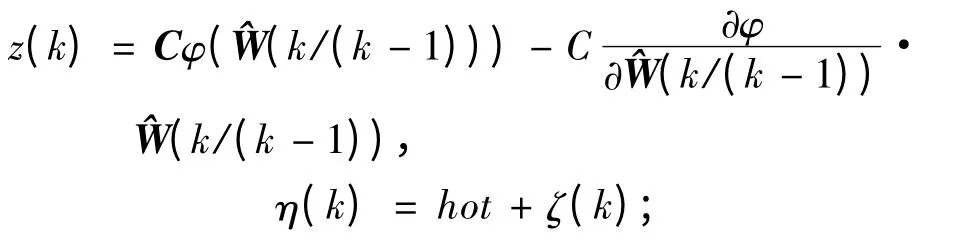
其中:hot 为泰勒级数展开的高阶项;η(k)为虚拟观测噪声，用以补偿线性化误差hot，它的时变统计特性为

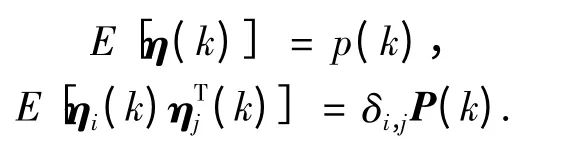
设隐层输出矩阵φ(v(k))关于权值W(k)的偏微分矩阵为Ω(k)，它是N×L 阶矩阵，可以表示为

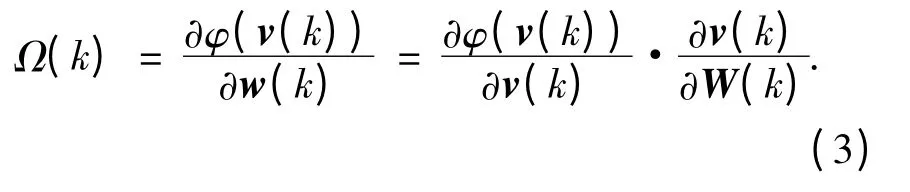
其中

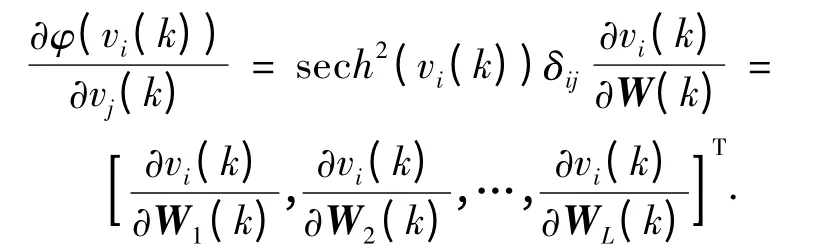
因此带未知噪声统计的非线性方程(1)和(2)的自适应卡尔曼滤波状态一步预测的递推公式为

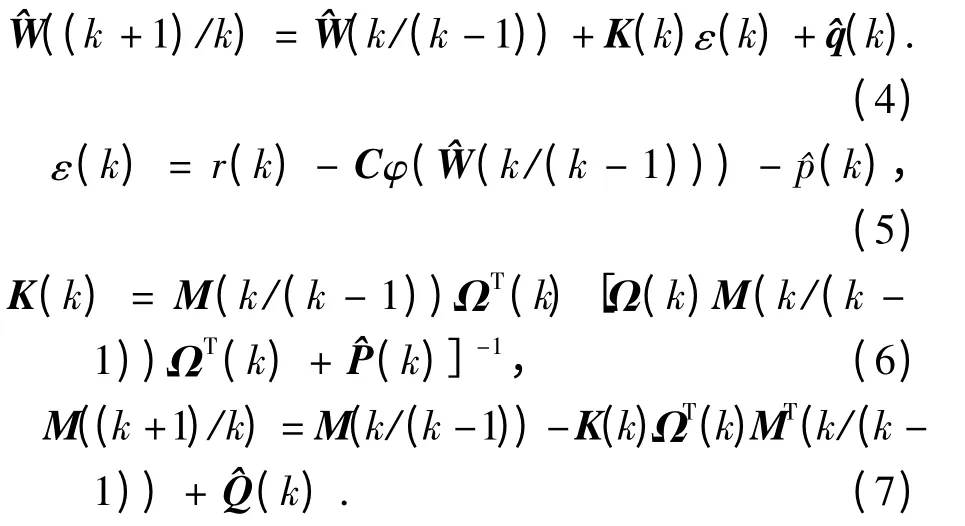
其中Ω(k)由式(3)定义，基于渐消记忆指数加权的噪声统计特性估值器为

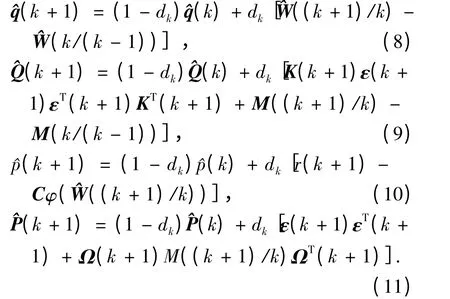
其中:

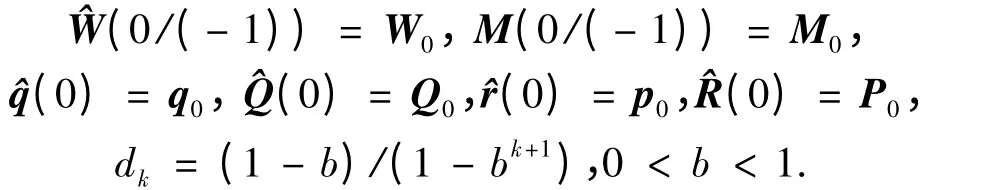
式中:b 为遗忘因子，其取值范围一般b ∈(0.95 ～1)，对于慢时变噪声b 取值较大，接近于1.则状态噪声统计估值的两段互耦自适应Kalman 滤波学习算法的程序流程为

步骤1 初始化权值向量W0，误差协方差矩阵M0，噪声统计估值q0，Q0，p0和P0;

步骤2 根据式(4)和式(5)计算k 时刻预测误差ε(k)和滤波增益矩阵K(k);

步骤3 根据式(6)和式(7)更新k+1 时刻的权值预测值和误差协方差矩阵M((k+1)/k);

步骤4 根据式(8)～(11)更新k+1 时刻时变噪声统计估计值，

步骤5 时刻k 递增准备下一时刻的窄带干扰预测抑制.

3 仿真结果

为了比较基于AKF 学习算法的RNNP 相对于自适应线性LMS 干扰预测器、自适应ACM 干扰预测器和基于RTRL 算法的RNNP 的抗干扰性能，进行了计算机仿真.首先，介绍输入信号的组成;其次，介绍衡量抗干扰性能的标准;最后，给出各种抗干扰技术的性能比较.

3.1 输入信号组成

仿真中的输入有用扩频序列采用15 级m 序列，环境噪声是方差为0.1 的加性高斯白噪声，干扰信号只考虑下面两种形式:

1)单频连续载波干扰(CWI).它是一种最为常见的干扰信号，例如射频干扰，CWI 时域上的数学表达式为j(k)=2sin(0.01k);

2)自回归干扰(ARI).它是由高斯白噪声递推产生的随机信号，其时域上的数学表达式为

j(k)=1.980 0j(k-1)-0.980 1j(k-2)+n0(k).其中n0(k)是方差为0.01 的高斯白噪声.

3.2 抗干扰性能标准

为了对各种预测器的抗干扰性能进行比较，主要参考下面两个性能指标:干噪比(JNR)改善量和信噪比(SNR)损失量，它们可以表示为

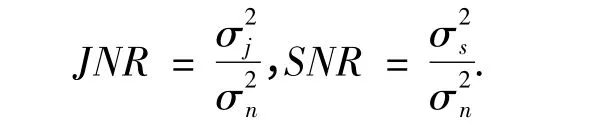
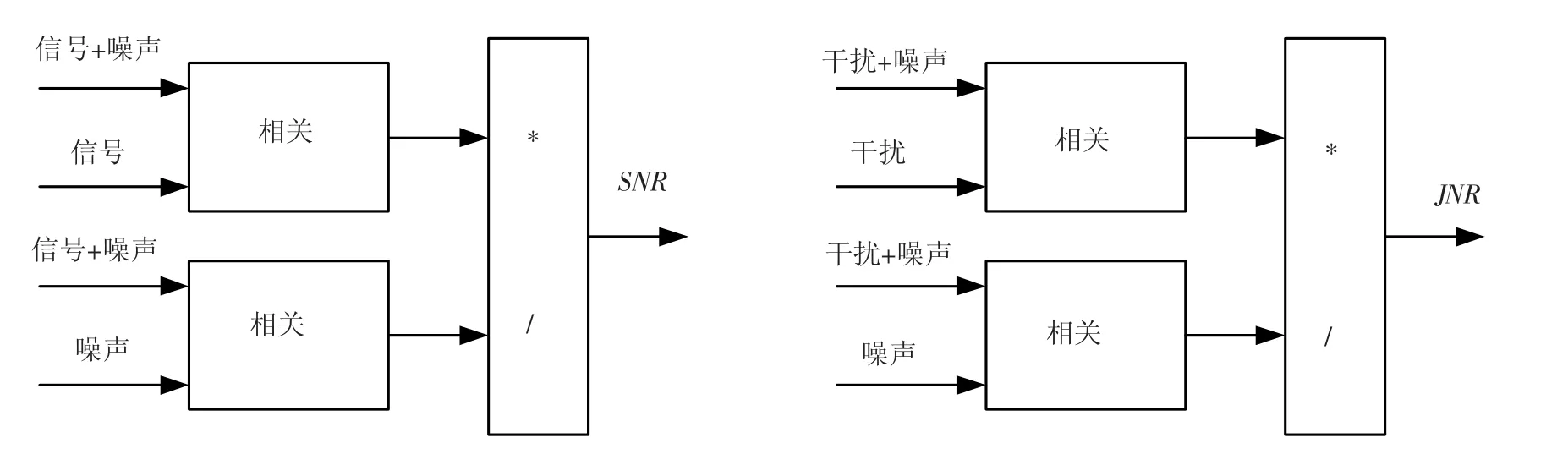
图3 仿真中SNR 和JNR 的计算方式

在上面仿真中，扩频信号与噪声及干扰与噪声的互相关很小，接近于零，可以忽略.所以信号+噪声与信号的互相关值表示信号的能量，干扰+噪声与干扰的互相关值表示干扰的能量，信号+噪声及干扰+噪声与噪声的互相关值都表示噪声的能量，所以通过图3 可以计算窄带干扰抑制技术的JNR 改善量和SNR 损失量，表示为

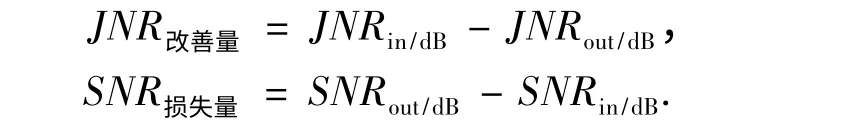
3.3 仿真结果与性能分析

RNNP 中输入层节点个数为4，隐层节点个数为5，输出层节点个数为1，输出层输入输出线性权值系数C=［1，1，1，1，1］，权值初始值为零，初始误差协方差矩阵为100E，其中E 为单位矩阵，噪声统计初始估计值为零或单位矩阵.图4 和图5 给出了当干扰分别为频率500 Hz 的CWI 和低频段的ARI 时，基于AKF 学习算法的RNNP 干扰抑制前后的信号的频谱图.可以看到，基于AKF学习算法的RNNP 能准确估计并消除混杂在接收信号中的强窄带干扰信号.

图6 和图7 给出了当干扰分别为CWI 和ARI时，基于AKF 学习算法的RNNP 干扰抑制前后的信号的伪码相关特性.可以看到，强窄带干扰存在时，伪码相关特性不再满足理想的相关特性，导致接收机无法正常工作，而基于AKF 学习算法的RNNP 能很大程度的抑制干扰信号，并且对有用扩频信号的损伤比较小，经过干扰抑制后，可以明显地在伪码相关曲线中码片延迟为511 chip 时发现相关峰值，使得接收机能够在强窄带干扰环境下正常捕获和跟踪扩频信号.

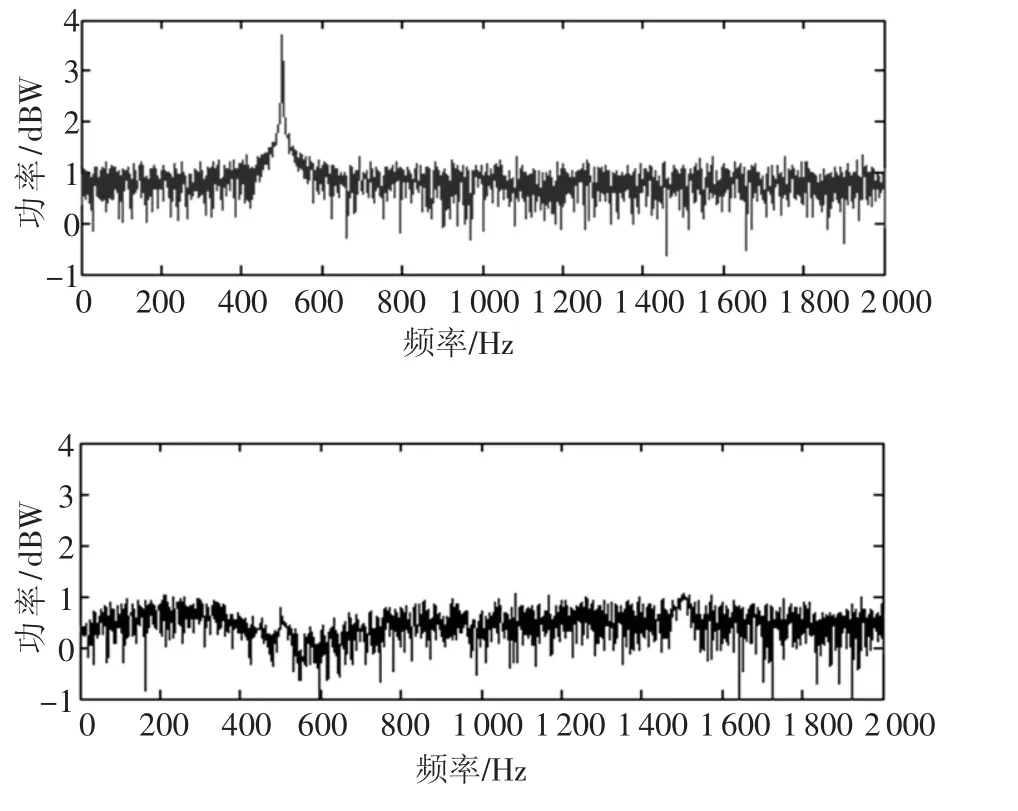
图4 CWI 及其干扰抑制前后效果

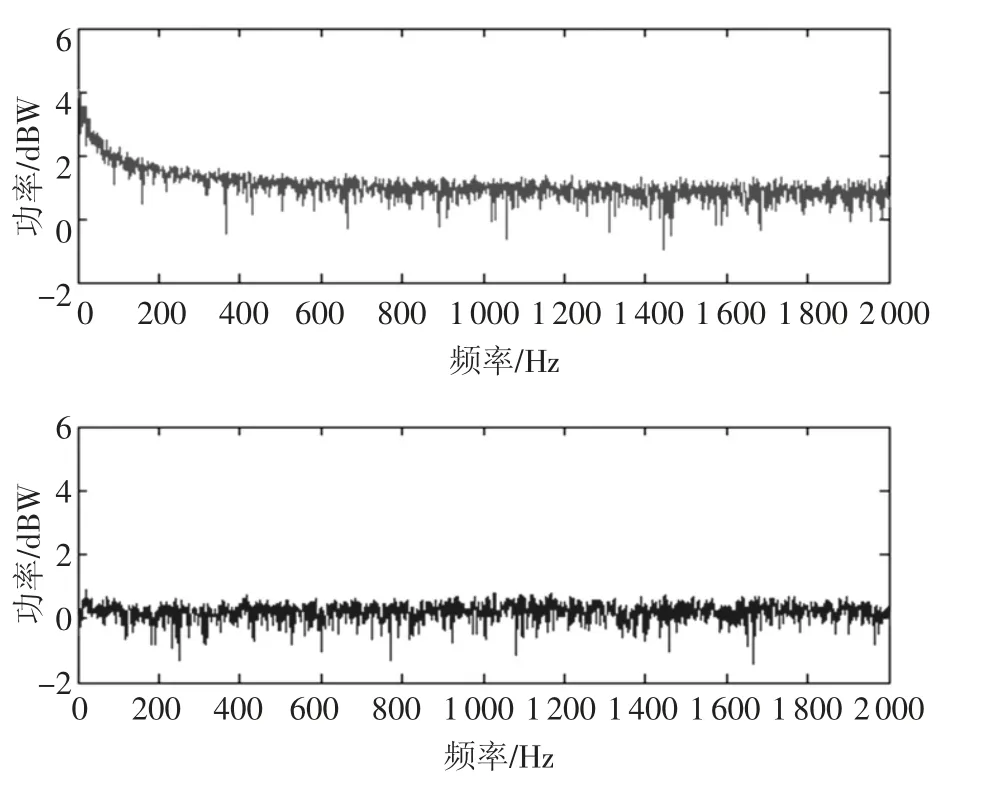
图5 ARI 及其干扰抑制前后效果

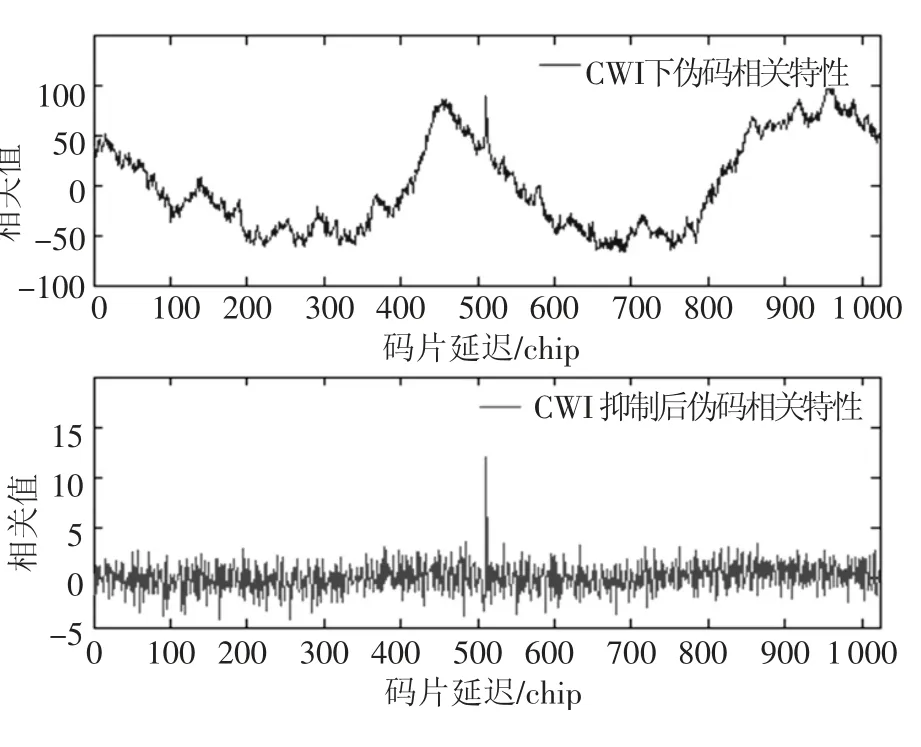
图6 CWI 抑制前后伪码相关特性

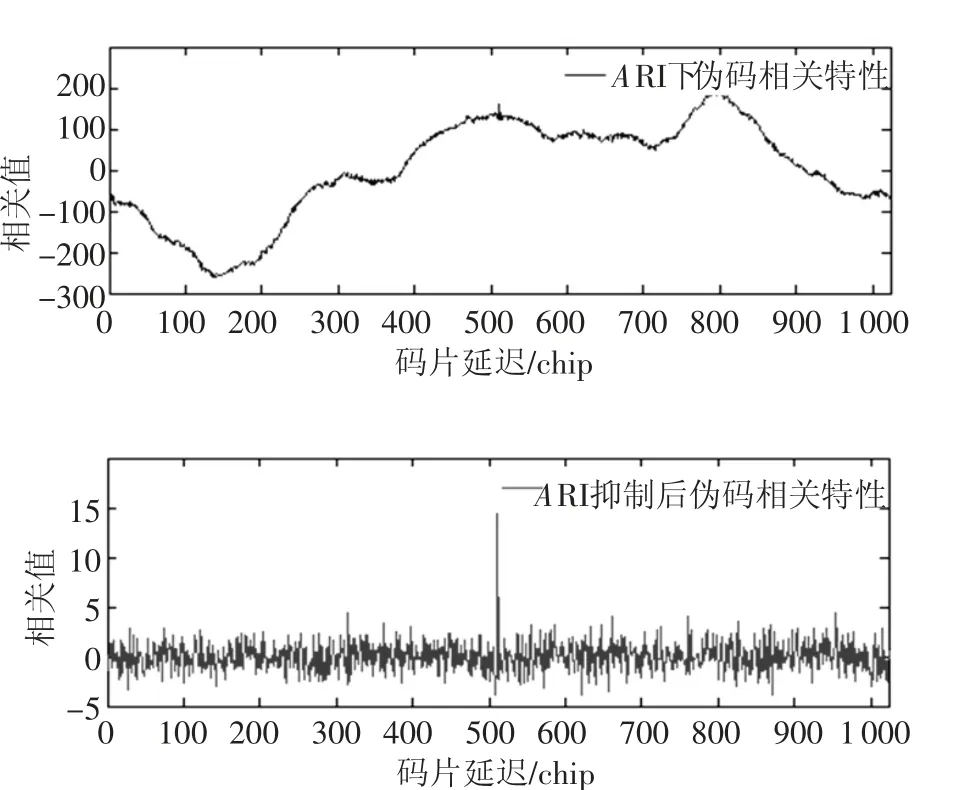
图7 ARI 抑制前后伪码相关特性

图8 和图9 给出了当干扰分别为CWI 和ARI时，基于AKF 学习算法的RNNP 误差输出的均方误差曲线.可以看到:1)基于AKF 学习算法的RNNP 的窄带干扰预测误差比其它干扰抑制技术要小的多，说明其干扰预测精度更高;2)基于AKF 学习算法的RNNP 的窄带干扰预测误差的收敛速度很快，可以实时地预测并抑制窄带干扰信号，大大改善了其它时域干扰预测抑制算法收敛速度慢和实时性差等缺点，可以适应于快时变干扰信道.

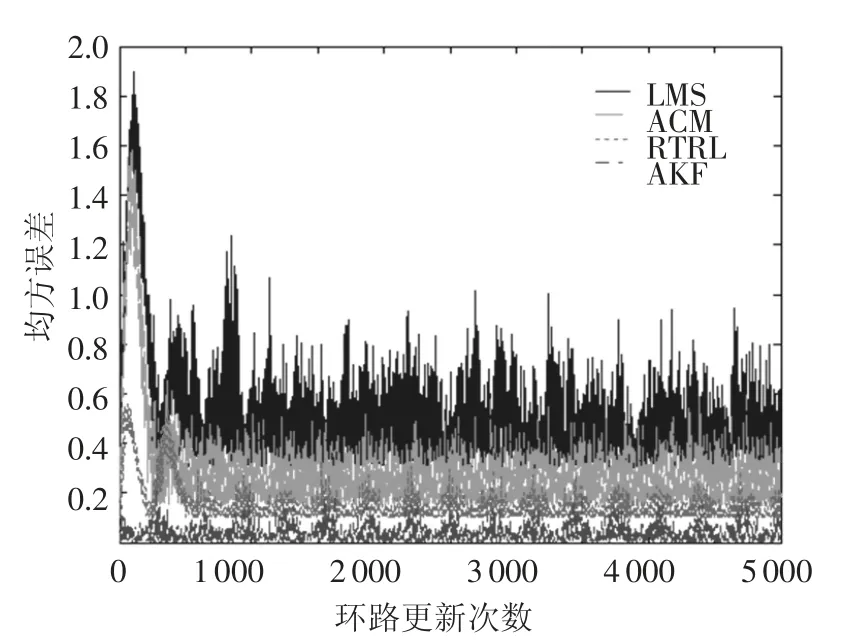
图8 CWI 抑制后的均方误差曲线

图9 ARI 抑制后的均方误差曲线

表1 和表2 给出了当干扰分别为CWI、ARI时，基于AKF 学习算法的RNNP 相对于其它干扰抑制技术的抗窄带干扰性能比较.其中自适应线性LMS 干扰预测器中延迟节点的个数为5，采用最小均方差(LMS)来反馈修改权值，收敛系数为0.000 1.自适应ACM 预测器中延迟节点个数为5，采用非线性近似条件均值(ACM)来反馈修改权值，初始收敛系数为0.001，初始估计方差为1，遗忘因子为0.9.基于RTRL 算法的RNNP 与AFK 算法的递归神经网络相同，权值初始值为零，初始误差协方差矩阵为100E，其中E 为单位矩阵.输入信噪比固定为-10 dB，输入干噪比是变化的，可以通过改变单频干扰信号幅值或改变噪声n0(k)的方差来改变干扰信号的能量.可以看到:1)当干扰为CWI 时，基于AKF 学习算法的RNNP 在干噪比改善量上相对于自适应LMS、ACM 和 RTRL 干扰抑制技术分别平均有15.4 dB，14.5 dB 和8.9 dB 的改善，而对于ARI干扰，分别有13.5 dB，12.2 dB 和6.2 dB 的改善.输入干噪比越大，干噪比改善量越大.2)当干扰为CWI 时，基于AKF 学习算法的RNNP 在信噪比损失量上比其它干扰抑制技术分别平均减少2.3 dB，1.4 dB 和0.7 dB，而对于ARI 干扰，分别平均减少2.6 dB，1.4 dB 和0.5 dB.输入干噪比越大，对有用信号的损伤越大.

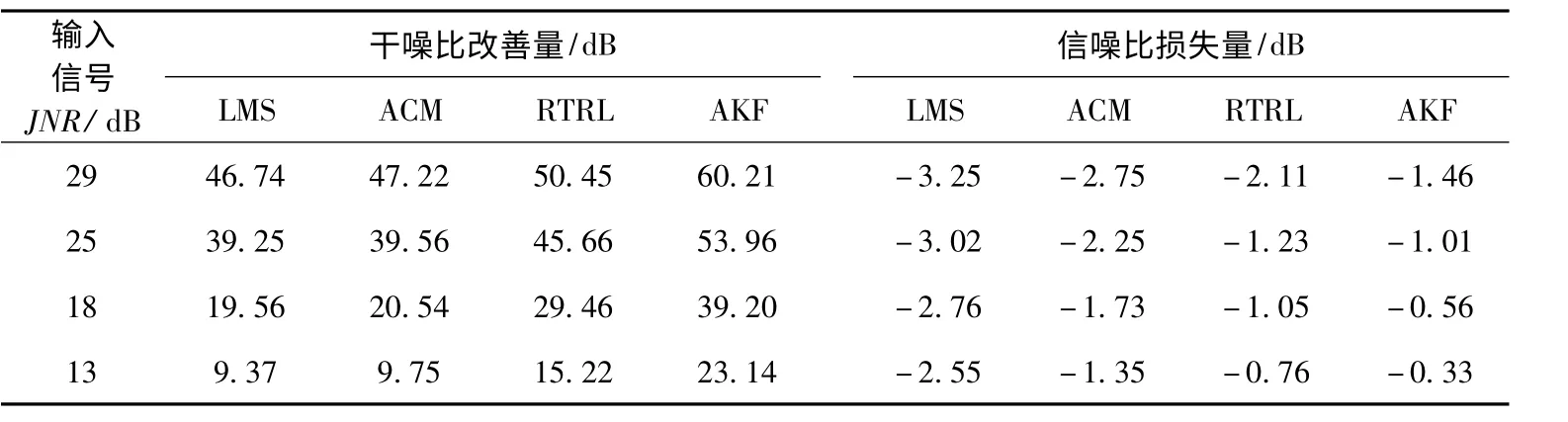
表1 CWI 下干噪比提高量和信噪比损失量

表2 ARI 下干噪比提高量和信噪比损失量

4 结 论

本文将基于渐消记忆指数加权的自适应卡尔曼滤波应用于递归神经网络的学习算法中，从而准确地预测并抑制扩频系统中的窄带干扰.该方法不需要已知信道参数，能够准确地预测窄带干扰信号，并且收敛速度相对于基于自适应LMS、ACM 算法和基于RTRL 算法的RNNP 的干扰抑制技术大大提高.仿真试验表明:当干扰信号为单频连续载波干扰(CWI)和自回归干扰(ARI)时，它的干噪比改善量和信噪比损失量相对于其它干扰抑制技术有不同程度的改善.

［1］PARKINSON B W，SPILKER J J.Global Positioning System:Theory and Applications:Volume I［M］.Reston:American Institute of Aeronautics and Astronautics，1996.

［2］ILTIS R A，MILSTEIN L B.An approximate statistical analysis of the widrow LMS algorithm with application to narrow-band interference rejection［J］.IEEE Transactions on Communications，1985，COM-33:10-19.

［3］VIJAYAN R，POOR H V.Nonlinear techniques for interference suppression in spread-spectrum systems［J］.IEEE Transactions on Communications，2004，38(7):1060-1065.

［4］CHANG Po-Rong，HU Jen-Tsung.Narrow-band interference suppression in spread-spectrum CDMA communications using pipelined recurrent neural networks［J］.IEEE Transactions on Vehicular Technology，1999，48(2):467-477.

［5］CHOI J，BOUCHARD M，YEAP T H.Decision feedback recurrent neural equalization with fast convergence rate［J］.IEEE Transactions on Neural Networks，2005，16(3):699-708.

［6］胡德文，王正志，王耀南，等.神经网络自适应控制［M］.长沙:国防科技大学出版社，2005.

［7］PARISI R，DI CLAUDIO E D，ORLANDI G，et al.Fast adaptive digital equalization by recurrent neural networks［J］.IEEE Transactions on Signal Processing，2007，45(7):2731-2739.

［8］MAO Wei-Lung.Novel SREKF-based recurrent neural predictor for narrowband/FM interference rejection in GPS［J］.International Journal of Electronics and Communications，2008，62(3):216-222.

［9］谢胜利，何昭水，高鹰.信号处理的自适应理论［M］.北京:科学出版社，2006.

［10］Steven M Kay.统计信号处理基础—估计与检测理论［M］.北京:电子工业出版社，2003.