MOTOMAN 机器人逆运动学新分析

王其军，杜建军

(哈尔滨工业大学 深圳研究生院，广东 深圳518055，jjdu@hit.edu.cn)

机器人现有的逆解求解方法主要有解析法［1-3］、几何法［4］、符号及数值方法［5］及近年出现的神经网络法［6-8］等.在机器人逆解过程中，一般在360°范围内计算机器人关节角度，但文献［2-3］在解关节角时采用单变量反正切函数，一个反正切函数的解可能被丢失.机器人反解有多解，但控制机器人只能有一组解，所以必须选取一组解作为最后确定的解，文献［2-3］中反解存在8 组解，没有给出怎样选取一组解作为最后反解的结果.

针对以上问题，本文在求关节变量时采用双变量正切函数，这样通过自变量的符号确定关节角度所在的象限，避免了解被丢失的可能性，针对反解多解，采用“最短行程”准则选取一组最接近于当前操作臂的解.

1 机器人运动学模型的建立

机器人运动学传统的描述方法是基于D-H方法［9］，用D-H 法建立了各杆坐标系如图1 所示，第i-1 系和i 系间的关系可以用坐标系的平移和旋转来实现.这种关系可由表示连杆i 对连杆i-1 相对位置的4 个齐次变换来描述，并叫做矩阵Ai.此关系式为

式中:θi为是关节i 的旋转角;βi为是关节i 和i+1 间的扭转角;ai为是关节i+1 的长度;di为是关节i 的偏距;i=0，1，2，…，6.

由六自由度机器人参考坐标系图，得到六自由度机器人的D-H 参数表如表1.

图1 机器人D-H 表示法参考坐标系

表1 D－H 参数

依照D-H 表示方法原理，可以得到坐标系X0-Z0到坐标系X1-Z1的变化矩阵为A1，同理相邻坐标系间的变化矩阵计为A2，A3，A4，A5，A6.这6 个坐标变化矩阵的表达式如下:

式中:Si=sin θi;Ci=cos θi，则

式中:

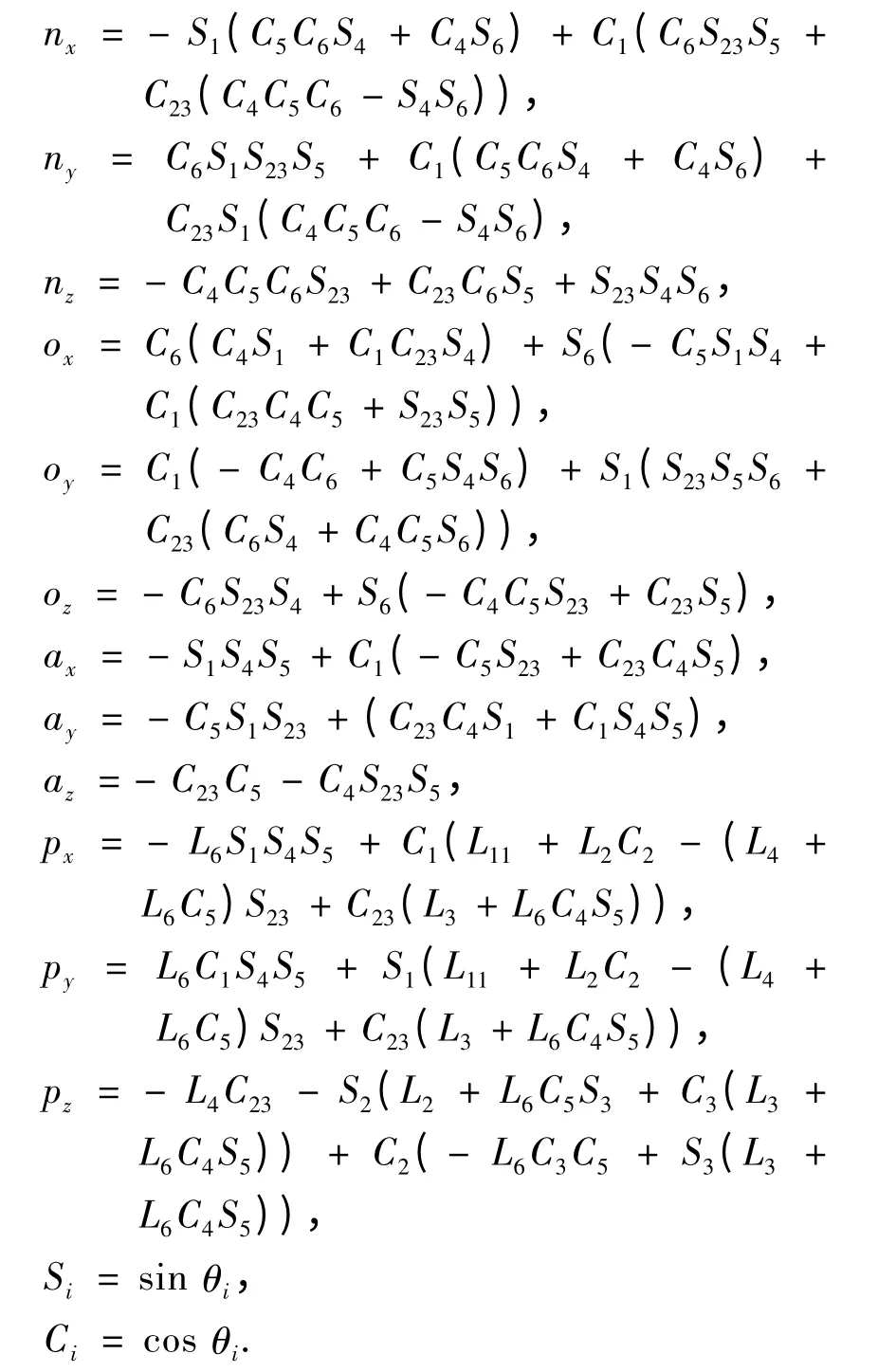
这样，由T 可以得到机器人末端的位姿(位置和姿态).

2 运动学反解

逆运动学问题是已知机器人末端执行器的位姿，求相应的关节变量.

将式(1)变形为

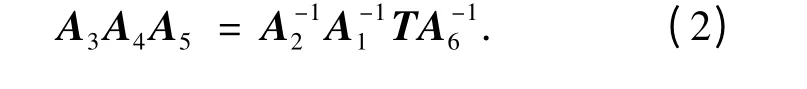
式(2)的左边

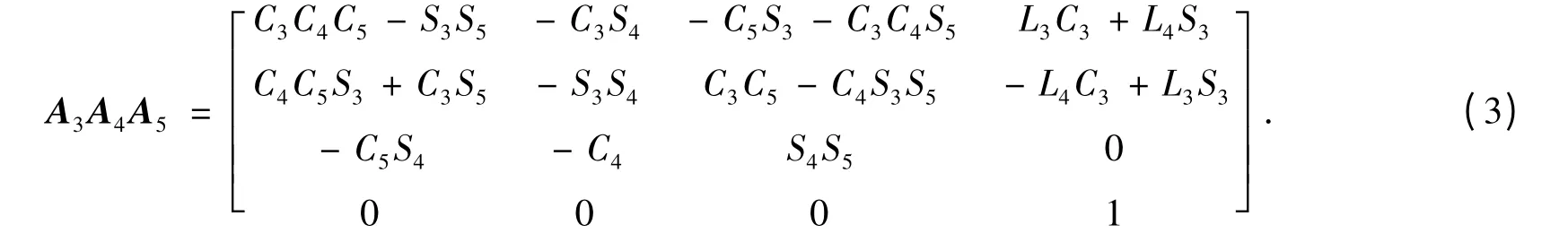
式(2)右边

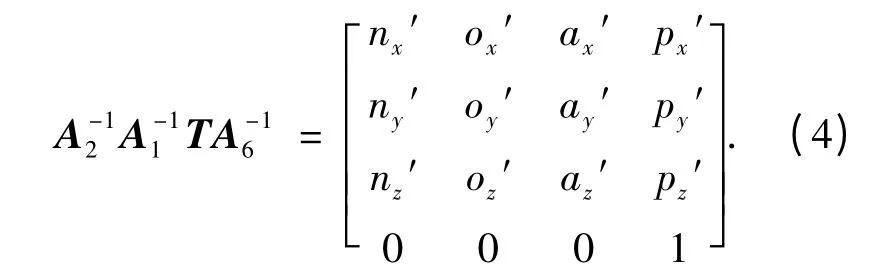
式中:

1)求解θ1.由式(3)与式(4)中的矩阵元素第三行第四列元素相等得到

θ1=Atan2(-ayL6+py，-axL6+px)或

θ1=Atan2(ayL6-py，axL6-px).

2)求解θ2.依据两边矩阵(3)，(4)中的第一行第四列元素和第二行第四列元素分别相等得到等式:

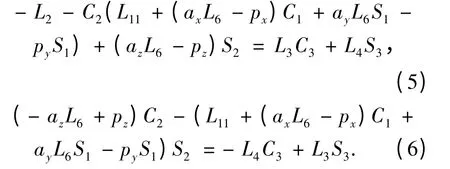
令

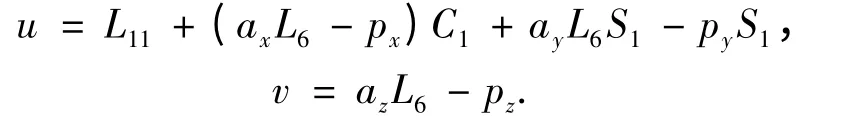
把u，v 代入式(5)、(6)得到

令

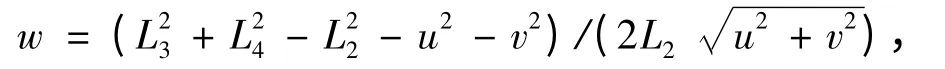
将式(7)与与(8)两边平方然后相加化简得到

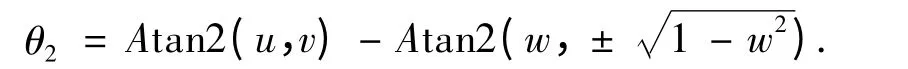
3)求解θ3.式(7)与(8)是关于S3与C3的方程组.所以可以解得

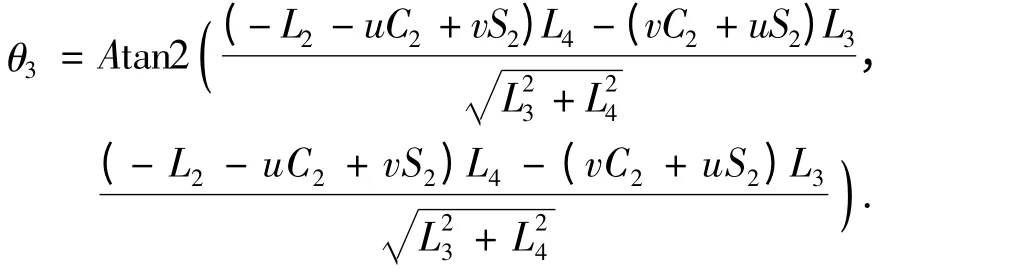
4)求解θ5.依据两边矩阵(2)，(3)中的第一行第三列元素和第二行第三列元素分别相等得到等式:

假设:

式(9)与(10)两边分别乘以S3与C3，然后相减，可以得到

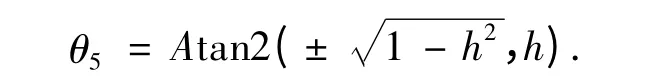
5)求解θ4.式(9)与(10)两边分别乘以C3与S3，然后相加得到

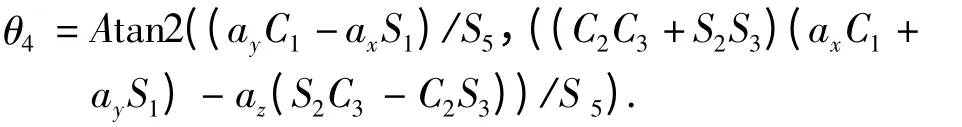
6)求解θ6.依据两边矩阵(2)，(3)中的第三行第一列元素和第三行第二列元素分别相等，可以得到

3 运动学反解不唯一性

从解的表达式中可以看到θ1，θ2，θ5分别有两个根，所以机器人有8 组根.在实际运行中，如何从机器人运动学的多组反解中选择一组合适的解是一个值得研究的问题.一般地，具有多组反解的机器人运动学问题可以采用优化算法来解决，定义一个优化准则，选择满足优化准则的最优解作为机器人运动学的确定反解.本文采用“最短行程”准则选取一组最接近于当前操作臂的解.算法流程图如图2 所示.

图2 最短行程准则流程图

4 验 证

按照如图3 所示的具体步骤，利用计算机程序进行计算，可以验证运动学解的正确性.

图3 运动学验证流程图

已知输入各关节角分别为-18.495 4，-37.618 3，-59.786 4，19.860 0，110.967 2，7.364 8，正解得到机器人位姿为387.217 0，-99.421 0，-104.717 0，180.000 0，-89.999 9，0.

逆解得到的关节角为-18.495 3，-37.618 3，-59.786 4，19.859 8，110.967 1，7.364 7.

计算结果表明，所得的解完全符合所赋初值.

5 结 论

2)在机器人逆解求关节角过程中，采用双变量反正切函数，通过自变量的符号就可以确定关节角度所在的象限，避免了解被丢失的可能性.

3)给出了六自由度机器人对应某一位姿的8个位行，采用“最短行程“准则选取一组最接近于当前操作臂的解.

4)本文提出的方法已经在深圳市元创兴科技有限公司自主研发的工业六自由度机器人中成功应用.

［1］PAUL R P，SHIMANO B E，MAYER G.Kinematic control equations for simple manipulations［J］.IEEE Trans SMC，1981，11(6):449-455.

［2］王雪松，许世范，郝继飞.MOTOMAN 机械手运动方程新的推导方法及求解［J］.中国矿业大学学报，2001，30(1):73-76.

［3］王奇志，徐心和.PUMA 机械手逆运动方程新的推导方法及求解.机器人.1998，20(2):81-87.

［4］FU K S，GONZALEZ R C，LEE C S G.Robotics Control Sensins Vision and Intelligence［M］.New York:McGrawHill，1987:78-82.

［5］MANOCHA D，CANNY J F.Efficient inverse kinematics for general 6R manipulators［J］.IEEE Transactions on Robotics and Automation，1994，10(5):648-657.

［6］KARLIK B，AYDIN S.An improved approach to the solution of inverse kinematics problems for robot manipulators［J］.Engineering Applications of Artificial Intelligence，2000(13):159-164.

［7］陈学生，陈在礼，谢涛.基于神经网络的机器人操作手IKP 精确求解［J］.机器人，2002，24(2):130-133.

［8］MAYROGA R V，SANONGBOOM.A radial basis function network approach for geometrically bounded manipulator inverse kinematics computation［J］//2003 IEEE/RSJ International Conference on Intelligent robots and system，2003，4(12):3564-3569.

［9］DENAVIT J，HARTENBERG R S.A kinematic notation for lower-pair mechanisms based on matrices［J］.ASM Journal of Applied Mechanics，1955，22(2):215-221.

［10］TAROKH M，KIM M.Inverse Kinematics of 7-DOF Robots and Limbs by Decomposition and Approximation［J］.IEEE Transaction on Robotics，2007，23(3):6-11.