高速线材减定径轧制变形特点与热模拟参数研究

曹 杰,刘雅政,阎 军,章 静

(1.北京科技大学材料科学与工程学院,北京 100083;2.安徽工业大学材料科学与工程学院,安徽 马鞍山 243002)

1 前言

现代高速线材轧机一般配备有减定径机组。减定径机组可提高高速线材轧机的生产作业率,满足用户对线材尺寸精度、表面质量、机械性能不断提高的要求。因此减定径轧制技术引起生产厂家的重视。高速线材减定径轧制具有轧制速度快、快速更换规格、重载或超重载等技术特点,可实现低温轧制,如摩根公司和达涅利公司现今设计的减定径机最低轧制温度都在 800℃以下,可以满足热轧的要求[1]。

配备减定径机组的高速线材轧机,其粗、中、(预)精轧机组孔型一般是所有规格共用一套孔型系统,所有规格产品都由减定径机组轧出,通过甩机架的办法实现不同规格产品的轧制。减定径机组孔型系统有多种,其中达涅利公司采用椭圆 -圆 -椭圆 -圆孔型系统。本文对该孔型系统的轧制变形特点进行分析,试图找寻合适的热模拟参数。

2 高速线材减定径轧制变形特点分析

2.1 有限元模型的建立

轧制产品的规格为 φ12 mm,孔型为椭圆 -圆 -椭圆 -圆孔型系统,四道次轧制。工艺参数的坯料、孔型尺寸与实际生产一致。

模型中轧辊视为恒温刚性体,轧辊表面温度取 200℃。初始条件主要是轧件的初始温度,初始温度取 750℃,均匀温度场。边界条件有摩擦条件和传热边界条件。轧辊与轧件接触面上采用库仑摩擦,摩擦系数取 0.2～0.3。传热边界条件包括轧件与周围环境的对流与辐射换热,轧件与轧辊接触时的接触传热。轧件与环境的对流换热系数取 0.02 kW/(m2·℃);轧件与环境间的辐射换热系数可根据辐射定律进行转换,热辐射率取 0.8;轧件与轧辊之间的接触热传导系数取15 kW/(m2·℃);轧件对称面采用绝热边界处理,即 q=0;由于金属变形和接触面的摩擦使轧件产生温升,其热功转换系数取 0.9。

为减少单元数量,节省计算时间,取 1/4轧件进行模拟。轧件材质取为 C22,材料的热物理性能参数和变形抗力模型取自 MARC材料库。单元类型选 8节点 6面体单元。为实现连轧,减少单元数量,缩短了机架间距。根据以上条件建立的有限元模型如图 1所示。

图 1 有限元模型

2.2 轧件变形程度分析

以等效塑性应变考察轧件的变形情况,K4～K1轧件的应变情况如图 2所示。

图 2 轧件断面等效塑性应变

由图 2可以看出,虽然减定径轧制的主要作用是控制成品的尺寸精度,但轧件仍然承受较大的变形量。单道次轧件的最大等效塑性应变在 0.4以上,轧件四道次累积的等效塑性应变范围为 1.097～1.890,轧件的变形渗透到中心。轧件中心的等效塑性应变大于外层的。但在 K3～K1道次,轧件表面以下的局部区域等效塑性应变达到最大值。

2.3 轧件温度变化

减定径轧制为高速轧制,变形和摩擦产生的热量会使轧件的温度升高。假设采用低温轧制,轧件初始温度为 750℃,K4～K1道次轧件变形后的温度分布如图 3所示。

图 3 轧件断面温度 (℃)分布

由图 3可以看出,每道次轧件断面的温度均大于初始温度 750℃。每道次轧件的最大温升≥15℃,轧件四道次累积温度升高为 49.4～76.7℃。轧件断面温升并不均匀,轧件中心温升较大,表面温升较小。K3～K1道次,轧件表面以下的局部区域温度达到最大值,这与等效塑性应变的分布相一致,可见温度升高主要是由变形引起的。

2.4 轧件变形速度分析

根据模拟计算的轧件尺寸和实际生产工艺规程中的轧制速度,计算终轧道次轧件的平均变形速度。轧制过程轧件平均变形速度可用式 (1)计算[2]。

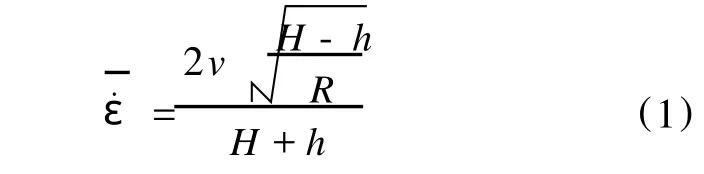
其中,H为轧件轧前高度;h为轧件轧后高度;R为轧辊半径;v为轧制速度。在孔型中轧制时,H、h、R用 Hc、hc、Rc的形式表示,分别表示轧件轧前平均高度、轧件轧后平均高度、轧辊平均工作半径。Hc可用轧件轧前面积与宽度的比值计算;hc可用轧件轧后面积与宽度的比值计算;Rc可用式 (2)计算。

式中,D为轧辊直径。按上述计算方法计算的各道次平均变形速度见表 1。

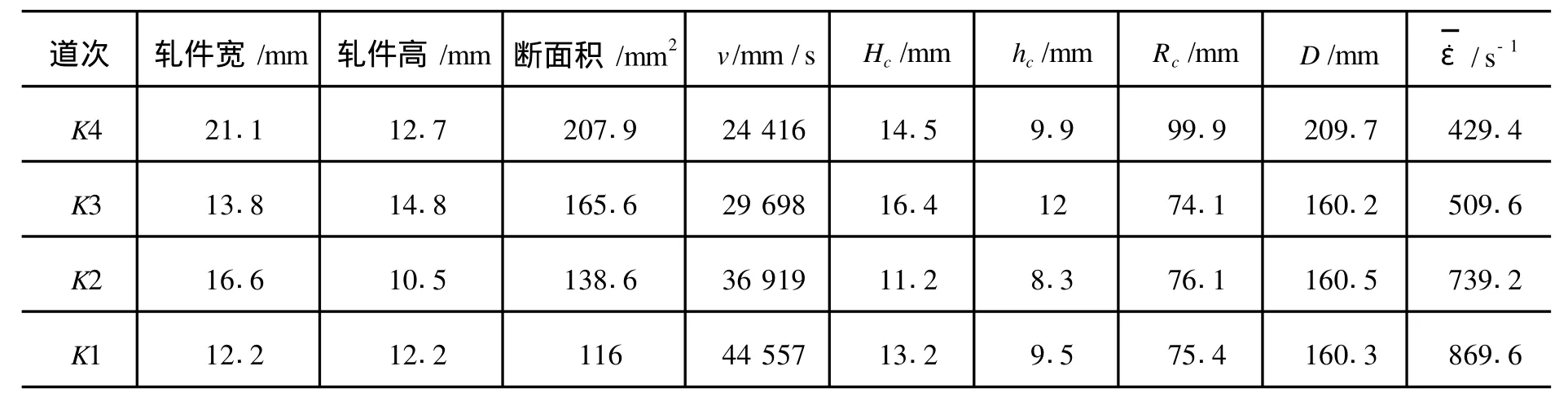
表 1 各道次平均变形速度

K4～K1道次平均变形速度分别为429.4 s-1、509.6 s-1、 739.2 s-1、869.6 s-1。可见减定径轧制变形速度相当高。

3 减定径轧制热模拟参数分析

3.1 减定径轧制的热模拟参数

在 Gleeble热模拟机上模拟轧制变形,需要确定的变形参数有变形温度 T、变形程度ε及变形速度等 。

变形温度 T可以取实际轧制的初始变形温度,但由于无法模拟高速变形造成的温升,所以对变形后轧件的温度也只能近似模拟。

减定径轧制变形程度可在 Gleeble热模拟机上较为准确地模拟。由于减定径轧制为高速轧制变形,机架间的时间间隔很短,可以把减定径轧制看成一次连续的变形。

3.2 减定径轧制热模拟实验变形程度的确定

通常,在 Gleeble热模拟机上可以采用压缩试样的方法模拟轧件变形。通过有限元模拟的方法确定了减定径轧制时轧件的变形程度,比如轧件四道次累积的等效塑性变形范围为 1.097～1.890。同样采用有限元模拟的方法可以模拟压缩试样的变形,确定变形量的大小。

根据热模拟试验条件,建立压缩试验的有限元模拟轴对称二维模型。有限元模型的建立的条件和过程与前面类似。试样为 φ8 mm×12 mm的圆柱状试样,变形温度为 750℃,压下速度为200 mm/s,取试样的 1/2模拟,采用剪切摩擦。试样上两点等效塑性应变与压缩量×100%)的关系如图 4所示。

试样的两端金属变形受工具影响,等效塑性变形差别较大。试样中间部分 (点 1、点 2所在区域)等效塑性应变差别较小,从点 1到点 2等效塑性应变逐渐减小。若以点 1到点 2等效塑性应变的范围对应于轧制时轧件断面的等效塑性应变范围,则 φ12 mm圆四道次减定径轧制轧件的变形程度与压缩量为 80%时的变形程度大致相当。

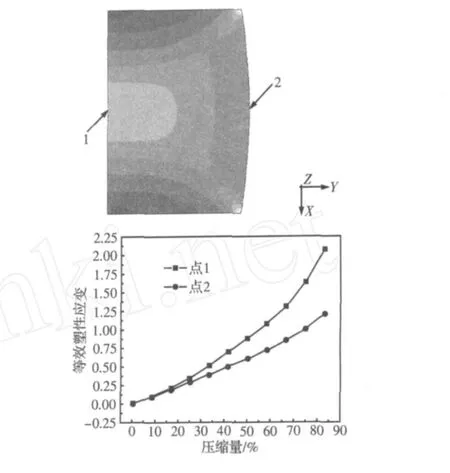
图 4 等效塑性变形与压缩量的关系

4 结论

(1)减定径轧制采用椭圆 -圆 -椭圆 -圆孔型系统,产品 φ12 mm圆四道次轧制累积的等效塑性应变范围为 1.097～1.890,温度升高为49.4～76.7℃。

(2)减定径轧制变形速度快,K4～K1道次平均变形速度分别为 429.4 s-1、509.6 s-1、739.2 s-1、869.6 s-1。

(3)减定径轧制变形程度可在 Gleeble热模拟机上较为准确地模拟,温度和变形速度只能近似模拟。

[1] 崔银会,张翠,李运虎.高速线材减定径机最新技术特点[J].马钢职工大学学报,2001,11(1):1-3.

[2] 赵志业.金属塑性变形与轧制理论 (二版)[M].北京:冶金工业出版社,1994,6.