周期混合信号和色关联噪声联合驱动下的单模激光随机共振

陈 培杰，汪志云

(襄樊学院 物理与电子工程学院，湖北 襄樊 441053)

周期混合信号和色关联噪声联合驱动下的单模激光随机共振

陈 培杰，汪志云

(襄樊学院 物理与电子工程学院，湖北 襄樊 441053)

研究周期混合信号和色关联噪声联合驱动下的单模激光系统的随机共振现象，运用线性近似的方法得到输出信号光强的功率谱和信噪比. 研究表明：信噪比都随泵噪声和量子噪声出现传统的随机共振现象；并讨论噪声的互关联时间和两信号的频率、振幅对信噪比的影响.

单模激光；随机共振；噪声；周期混合信号

近30年来，非线性系统中存在随机共振的动力学现象引起了人们的普遍关注，随机共振研究在理论和实验上都取得了较大的进展[1-3]. 激光系统中的随机共振现象也引起了人们的浓厚兴趣，曹力等人[4-14]运用线性近似的方法，首次将信号与考虑关联的泵噪声和量子噪声相乘的形式引入单模激光系统，在激光系统中发现了信噪比随关联强度的变化出现单峰的随机共振，并深入研究了具有信号调制噪声、调幅波和调频波在各种关联噪声驱动下单模激光系统的随机共振.

以上研究工作都是采用单周期信号，对于多周期信号激励下激光系统的随机共振至今没有研究. 但多周期信号激励的双稳态系统中的随机共振现象，也有了较为深入地研究，如周丙常等[15]研究了周期混合信号和噪声联合激励下的非对称双稳态系统的随机共振现象，发现对于基频和高阶谐频情形下均出现随机共振. 本文主要研究周期混合信号和指数关联的噪声共同驱动单模激光模型，得到信号的输出光强信噪比随噪声强度的变化情况，及两个输入信号的振幅和频率对信噪比值的影响.

1 混合信号和白噪声联合驱动下的单模激光信噪比

单模激光增益模型输入周期混合信号后的光强郎之万方程为:

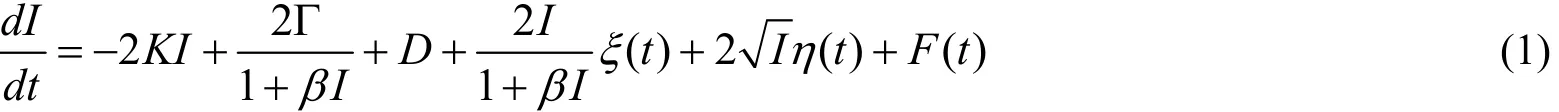
式(1)中，I为激光光强，β和Γ分别为自饱和系数和增益系数，K为损失系数，F(t)为周期混合信号

A1和A2分别为两信号的振幅，Ω1和Ω2分别为两信号的频率，ξ(t)和η(t)分别为泵噪声和量子噪声，其统计性质为：

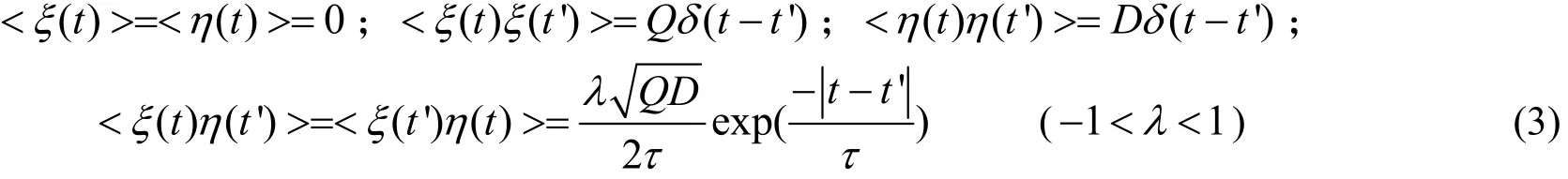
式(3)中，Q和D分别为泵噪声和量子噪声的噪声强度，τ为噪声互关联时间，λ为噪声关联参数. 令I(t)=I+ε(t) ε(t)为微扰项，代入(1)式，并在定态光强I=Γ−K附近对(1)式线性化，可得到线性化方程：

00βK

由式(4)可解得：

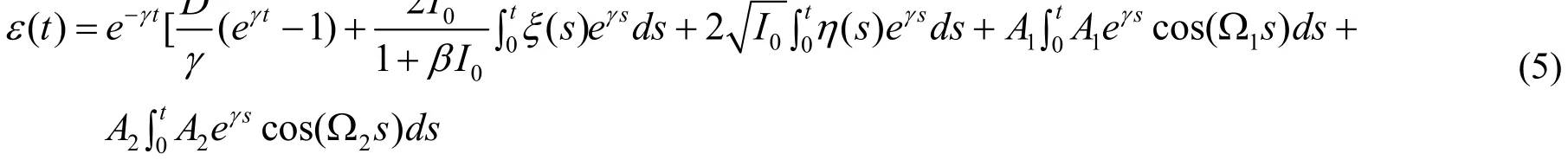
由(3)式和(5)式可以求得<ε(t)>，<ε(t+t')>和<ε(t)ε(t+t')>.根据平均光强相关函数的定义：

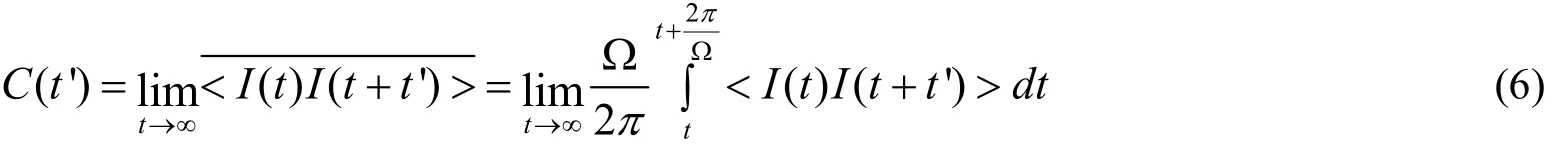
现假设输出信号中所含的谐波主要是由输入的两种频率(Ω1、Ω2)成份构成，而忽略高阶谐频的情形，则可得到平均光强相关函数(γ≠τ−1)：将式(7)进行傅利叶变换，得到光强功率谱为：式中S1(ω)为输出信号功率谱，S2(ω)为输出噪声功率谱，具体表达式为：

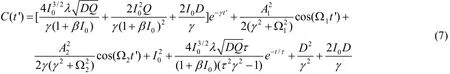
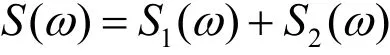
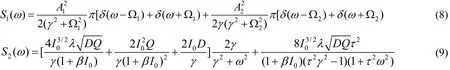
由(8)式和(9)式可知，输出信号功率谱中的二个信号频率(Ω1、Ω2)处的单位噪声功率分别为输出信号的总功率为将输出信号功率与输出噪声功率之比定义为信噪比(取正ω的谱)，即可以得到输出信号的信噪比为

2 输出信号光强的随机共振

下面主要讨论泵噪声强度Q、量子噪声强度D和互关联时间对由输入的两种频率(Ω1、Ω2)为主要成份构成的输出信号对信噪比(SNR)的影响，以及其中一个输入信号的振幅和频率对信噪比的影响.

在图1中，画出了输出信号的信噪比分别作为泵噪声强度Q和量子噪声强度D的函数随不同的噪声关联系数λ变化的曲线. 从图中可以看到：当λ≥0时，输出信号光强的信噪比值曲线都是单调衰减，没有出现随机共振现象；当λ<0时，输出信号的信噪比(SNR)随Q和D曲线都出现了峰值，信噪比随泵噪声强度的变化出现随机共振现象，且当λ绝对值越大，共振峰越高，并其位置向Q(或D)增大的方向移动，这与单周期信号作用的结果相同.

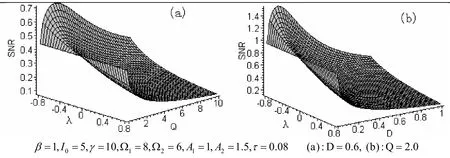
图1 信噪比SNR随量子噪声强度D和泵噪声强度Q的变化

图(2)是信噪比与噪声互关联时间τ和泵噪声强度Q的变化情况，从图中可以看出：信噪比随Q的变化出现随机共振现象；当Q取一定的值时，信噪比随互关联时间τ的增长而减小，信噪比随Q变化的共振峰随τ的增大而减小，且位置相同. 由于当τ趋近于0时，色关联噪声过渡到白关联噪声，这也说明了白关联噪声引起的随机共振现象比色关联噪声要明显.

图3(a)是输出信号光强的信噪比SNR随输入信号的振幅和泵噪声强度Q的变化曲线，由图可知：当2A取较小的值时，信噪比SNR随Q 单调变化，并没有出现随机共振现象；而随着2A值的增大，信噪比不断增大，且随泵噪声强度Q的变化出现了共振峰，存在随机共振现象，且不同的2A值，峰值的位置都相同，即所对应的为同一泵噪声强度Q值. 由图3(b)中可知，当噪声强度和输入信号的频率一定时，信噪比随两输入信号的振幅单调增加.

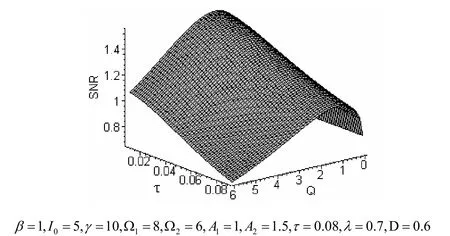
图2 信噪比SNR随噪声互关联时间τ和泵噪声强度Q的变化

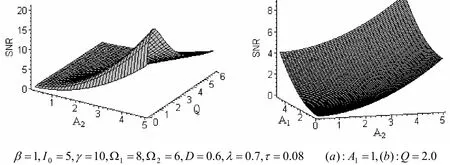
图3 信噪比SNR随振幅2A和泵噪声强度Q的变化

图4(a)信噪比SNR和两信号的频率的变化曲线. 由图可知：在2Ω取一定值的情况下，信噪比随Q的变化出现了随机共振现象，振峰的位置随Q的增大而右移；随着2Ω的增大，信噪比的峰值越小. 图4(b)中给出了当噪声的强度一定时，信噪比随两个输入信号的频率之间的关系曲线. 从图中可以看出，信噪比随2Ω和1Ω单调变化，都随频率的的增大而减小. 这与文献[15]中得出的结论是相同的，即谐频阶数越高、非对称双稳态的输出信噪比随噪声强度的变化共振曲线的共振峰越低.

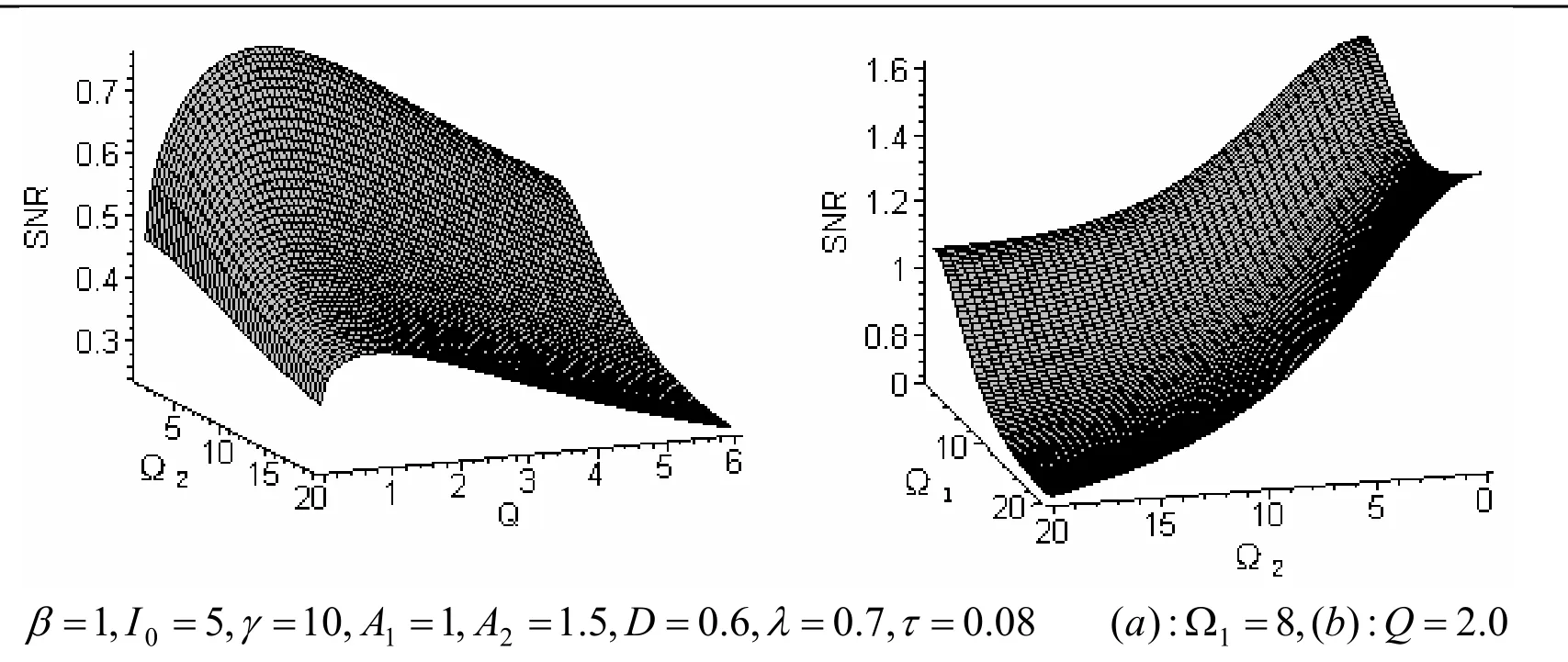
图4 信噪比SNR随频率1Ω、2Ω和泵噪声强度Q的变化

3 结语

本文研究了周期混合信号和色关联噪声联合驱动下单模激光输出光强的随机共振现象. 当λ为负值时，信噪比随泵噪声强度Q和量子噪声强度D的变化都出现了的随机共振现象. 两输入信号的振幅和频率对输出的信噪比都产生了影响，在实际的激光系统中，输入的信号往往是多频率成份，这些频率成份在随机共振过程中所起的作用至今尚未完全解决. 引入双周期信号作用于单模激光系统的研究，不仅对处理多频率信号激励下的激光系统提供了很好的研究思路和方法，还可以通过调控两输入信号的振幅和频率，来对激光系统共振现象进行调控，在优化激光通讯系统的实验研究方面提供理论依据.

[1] 刘 立, 吴大进. 随机共振研究新进展[J]. 大学物理, 2009, 28(9): 46-50.

[2] 祝恒江, 吴锡田. 随机共振研究进展[J]. 大学物理, 1997, 16(7): 28-31.

[3] 胡 岗. 随机力与非线性系统[M]. 上海：科技教育出版社, 1994: 219-254.

[4] 程庆华, 曹 力, 吴大进. 信号调制泵噪声和实虚部间关联量子噪声驱动下单模激光的随机共振[J]. 物理学报, 2004, 53(8): 2556-2562.

[5] 韩立波, 曹 力, 吴大进, 等. 偏置信号调制下色关联噪声驱动的单模激光的光强相对涨落[J]. 物理学报, 2004, 53(10): 2127-2132.

[6] 许德胜, 曹 力, 吴大进. 平方泵噪声驱动的单模激光立方模型及光强定态概率分布[J]. 物理学报, 2006, 55(02): 0692-0695.

[7] 程正则, 吴子瑕, 曹 力, 等. 信号调制下单模激光增益模型的动力学性质[J]. 华中科技大学学报, 2007, 35(10): 67-69.

[8] 张良英, 曹 力, 吴大进. 单模激光线性模型初态的随机共振[J]. 华中科技大学学报, 2004, 32(2): 106-108.

[9] 张良英, 曹 力, 吴大进. 单模激光线性模型瞬态的随机共振[J]. 华中科技大学学报, 2004, 32(12): 103-105.

[10] 张良英, 曹 力, 金国祥. 调幅波的单模激光线性模型随机共振[J]. 物理学报, 2006, 55(12): 6238-6212.

[11] 张良英, 金国祥, 曹 力. 调频的单模激光线性模型随机共振[J]. 物理学报, 2008, 57(08): 4706-4711.

[12] 张良英, 曹 力, 金国祥. 色噪声驱动下调幅波的单模激光随机共振[J]. 物理学报, 2007, 56(9): 5093-5097.

[13] 张良英, 曹 力. 信号调制噪声的单模激光随机共振[J]. 华中科技大学学报, 2005, 33(8): 119-120.

[14] 张良英, 曹 力, 吴大进. 指数形式关联噪声驱动下单模激光线性模型的随机共振[J]. 中国激光, 2004, 31(1): 53-56.

[15] 周丙常, 徐 伟. 周期混合信号和噪声联合激励下的非对称双稳系统的随机共振[J]. 物理学报, 2007, 56(10):5623-5628.

Stochastic Resonance in Single-mode Laser Driven by M ixed Signal Periodic and Noises w ith Color Cross-Correlation

CHEN Pei-jie，WANG Zhi-yun
(School of Physics and Electronic Engineering, Xiangfan University, Xiangfan 441053, China)

It probed the phenomenon of stochastic resonance (SR) in single-mode laser driven by mixed signal periodic and noises w ith color cross-correlation is investigated. The intensity power and signal-to-noise ratio (SNR) of signal is derived using the linear approximation method. The result shows that the resonance of SNR appeared w ith the change of intensities of the pump noise and quantum noise; and the influence on SNR from the correlation time between noises and frequency and amplitude of m ixed signal periodic was also discussed.

Single-mode Laser; Stochastic Resonance; Noises; M ixed periodic signal

O414

A

1009-2854(2010)08-0016-04

（责任编辑：饶 超）

2010-07-10;

2010-08-09

陈培杰(1975— ), 女, 湖北枣阳人, 襄樊学院物理与电子工程学院讲师.