基于离散Hopfield神经网络的高校科研能力评价模型
2010-11-07何黎
何 黎
(武汉科技大学 管理学院,湖北武汉430081)
基于离散Hopfield神经网络的高校科研能力评价模型
何 黎
(武汉科技大学 管理学院,湖北武汉430081)
本文将高校科研能力分为很强(Ⅰ)、较强(Ⅱ)、一般(Ⅲ)、较差(Ⅳ)及很差(Ⅴ)五种状态,将通过预测的20所高校科研能力指标及相对应的等级状态作为输入节点构建基于离散Hopfield神经网络的评价模型。并将另5所高校的相关数据输入进行仿真实验,结果表明该模型能较好地对高校科研能力进行评价,但对优劣势并存且都很突出的高校,该模型无法作出有效评价。
离散Hopfield;高校科研能力
一、引言
目前,作为高校核心能力的科研能力,其高低已经成为衡量一所高校综合实力的重要指标。它不仅影响着高校自身的发展,也对高校所在地区的经济发展产生很大影响。影响科研能力的因素众多,且相互交叉互相影响,无法用确定的数学模型进行描述。目前,对高校科研能力评价的方法很多,但普遍存在工作繁琐、时间滞后等缺点。因此,如何准确评价高校科研能力已经成为摆在政府、企业和高校面前一个十分重要的问题。
二、离散Hopfield神经网络概述
1.网络结构
Hopfield神经网络及学习算法最初是由美国物理学家J.J Hopfield于1982年首先提出的,它作为一种全连接型的神经网络,曾经为人工神经网络的发展开辟了新的研究途径。Hopfield最早提出的网络是二值神经网络,神经元的输出只取1和-1,所以也称离散Hopfield神经网络(DHNN,Discrete Hopfield Neural Network)。在离散Hopfield网络中,所采用的神经元是二值神经元,因此所输出的离散值1和-1分别表示神经元处于激活和抑制状态,它是一种单层、输出值为二值的反馈网络。
以一个由三个神经元组成的Hopfield神经网络为例,其结构如下图1-1所示:

图1-1
图中第0层仅作为网络的输入,它不是实际的神经元,所以没有计算功能;第一层是神经元,故而执行对输入信息与权系数的乘积求累加和,并经非线性函数f处理后产生输出信息。f是一个简单的阀值函数。如果神经元的输出信息大于阀值θ,那么神经元的输出取值为1;小于阀值θ,则神经元的输出取值为-1。

其中xj为外部输入,且有:

一个DHNN的网络状态是输出神经元信息的集合,对于一个输出层是n个神经元的网络,其t时刻的状态为一个n维向量:
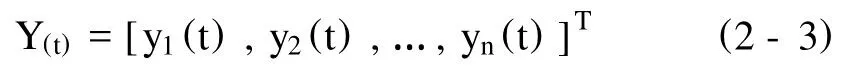
Yi(t)(i=1,2,…,n)可以取值为1或-1,故n维向量Y(t)有2n种状态,即网络有2n种状态。考虑DHNN的一般节点状态,用yi(t)表示第j个神经元,即节点j在时刻t的状态,则节点的下一个时刻(t+1)的状态可以求得:
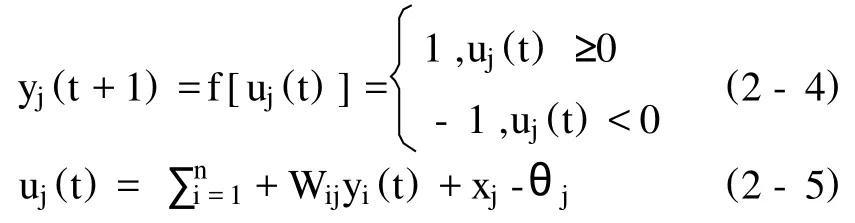
2.网络工作方式
Hopfield网络按动力学方式运行,其工作过程为神经元状态的演化过程,即从初始状态按“能量”(Lyapunov函数)减小的方向进行演化,直到达到稳定状态,稳定状态即为网络的输出。其主要的工作方式有两种:
①串行(异步)工作方式。在任一时刻t,只有某一神经元i(随机的或确定的)依式(2-4)与(2 -5)变化,而其他神经元的状态不变。
②并行(同步)工作方式。在任一时刻t,部分神经元或全部神经元的状态同时改变。
3.网络的稳定性
从DHNN的结构可以看出:它是一种多输入、含有阀值的二值非线性动态系统。在动态系统中,平衡稳定状态可以理解为系统某种形式的能量函数在系统运动过程中,其能量值不断减小,最后处于最小值。
Coben和Grossberg在1983年给出了关于Hopfield网络稳定的充分条件,他们指出:如果Hopfield网络的权系数矩阵W是一个对称矩阵,并且对角线元素为0,则这个网络是稳定的。即在权系数矩阵W中,如果
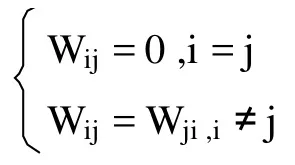
则Hopfiled网络是稳定的。
以上只是Hopfield网络稳定的充分条件,而不是必要条件。在实际中有很多稳定的Hopfield网络,但它们并不满足权系数矩阵W是对称矩阵这一条件。
三、离散Hopfield神经网络学习规则
离散Hopfield神经网络学习规则的关键点是其权系数矩阵的设计方法。常用的设计方法有:外积法和正交化法。
设计权系数矩阵的目的是:
①保证系统在异步工作时的稳定性,即它的权值是对称的;
②保证所有要求记忆的稳定平衡点都能收敛到自己;
③使伪稳定点的数目尽可能少;
④使伪稳定点的吸引力尽可能大。
1.外积法
对于一给定的需记忆的样本向量{t1,t2,…, tn},如果tk的状态为+1或-1,则其链接权值的学习可以利用“外积规则”,即

利用外积法设计离散型Hopfield的步骤可归结为:
步骤1:根据需要记忆的样本,按式(2-1)计算权系数矩阵。
步骤2:令测试样本pi(i=1,2,…,n)为网络输出的初始值yi(0)=pi(i=1,2,…,n),设定迭代次数。
步骤4:当达到最大迭代次数或神经元输出状态保持不变时,迭代终止;否则返回步骤3继续迭代。
2.正交化法
MATLAB神经网络工具箱中newhop()函数采用的权值修正方法即为正交化法,调整步骤如下:
步骤1:输入N个输入模式t={t1,t2,…,N-1, tN}及参数ζ,h。
步骤2:计算A={t1-tN,t2-tN,…,tN-1-tN}。
步骤3:对A做奇异值分解A=USVT,并计的秩K=rank(A)。
步骤4:分别由Up={U1,U2,…,UK}和um= {uk+1,uk+2,…,un}计算
步骤5:计算Wt=Tp-ζ*Tm,bt=tN-wt*tN。
步骤6:计算W=exp(h*Wt)。
四、高校科研能力评价模型
影响高校能力的因素很多,本文以较为重要的11个影响因素作为评价指标:科研队伍(X1)、科研基地、科技学识及相应的载体(图书情报资料)、科研经费、科研管理、信息接收加工能力、学识积累与技术储备能力、科研技术创新能力、知识释放能力、自适应调节能力、科学决策能力。
高校科研能力分为五个等级:很强(Ⅰ)、较强(Ⅱ)、一般(Ⅲ)、较差(Ⅳ)及很差(Ⅴ)。将若干个典型的分类等级所对应的评价指标设计为离散型Hopfield神经网络的平衡点,Hopfield神经网络学习过程即为典型的分类等级的评价指标逐渐趋近于Hopfield神经网络平衡点的过程。学习完成后,Hopfield神经网络储存的平衡点即为各个分类等级所对应的评价指标。当有待分类的高校的评价指标输入时,Hopfield神经网络即利用其联想记忆的能力逐渐趋近与某个储存的平衡点,当状态不再改变时,此时平衡点所对应的便是待求的分类等级。主要步骤如下图4-1所示

图4-1-1
1.设计理想的等级评价指标
本文所研究的20所高校的科研能力等级与11个评价指标之间的关系,如下表4-1-1所列:

表4-1-1
将各个等级的样本对应的各评价指标的平均值作为各个等级的理想评价指标,即作为Hopfield神经网络的平衡点,如表4-1-2所示:
2.理想的等级评价指标编码
离散型Hopfield神经网络神经元的状态只有1和-1两种,所以将评价指标映射为神经元的状态时需要将其进行编码。
编码规则:当大于或等于某个等级的指标值时,对应的神经元状态设为“1”,否则为“-1”。理想的5个等级评价指标编码如下图4-2-1所列:●表示神经元状态为“1”,即大于或等于对应等级的理想评价指标值,反之则用○表示。
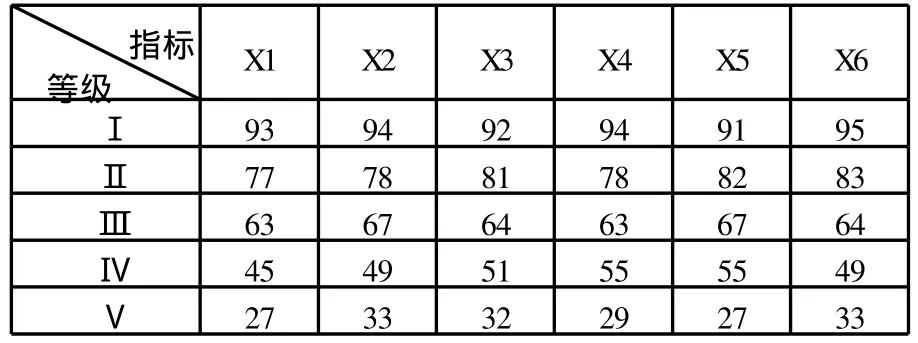
表4-1-2

图4-2-1
3.待分类的等级评价指标编码
5所待分类的高校等级评价指标如表4-3-1所示,根据上述的编码规则得到对应的编码如表4-3-1所示。
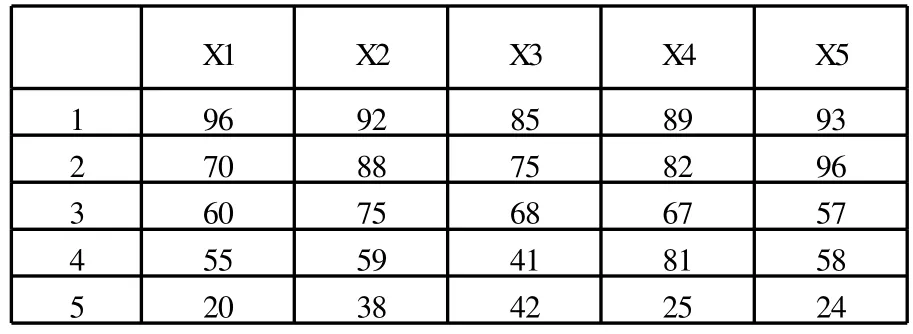
表4-3-1

图4-3-1
4.创建网络
利用MATLAB自带的神经网络工具箱函数创建离散型Hopfield神经网络理想的5个等级评价指标编码为5个11*5的矩阵,每个矩阵只包含“1”和“-1”两种取值。数据保存在class.mat文件中,以此为class_1、class_2、class_3、class_4和class_5。
待分类的5所高校等级评价指标的编码保存在sim.mat文件中,5个编码矩阵分别为sim_1、sim_2、sim_3、sim_4和sim_5。

5.仿真、分析
网络创建完毕后,将待分类的5所高校等级评价指标的编码作为Hopfield神经网络的输入,经过一定次数的学习,利用MATLAB自带的sim函数进行仿真便可以得到结果。将仿真结果与真实的等级进行比较,可以对该模型进行合理的评价。
仿真结果如下图4-5-1所示:
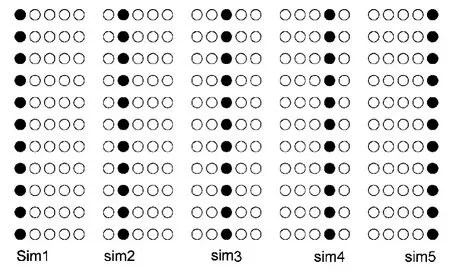
图4-5-1
五、结果分析
分别与前文图4-2-1,图4-3-1对应,可以看出,设计的Hopfield网络能够有效地进行分类从而对高校的科研能力进行客观公正地评价。
但本文所设计的Hopfield神经网络并非适用与任何场合。当某所高校的优势与劣势并存且相当明显(例如:某些影响因素得分很高,另一些得分很低)时,Hopfield神经网络将得不到确切的分类。
[1]张良均,曹晶,蒋世忠.神经网络实用教程[M].北京:机械工业出版社,2008.
[2]吴简彤,王建华.神经网络技术及应用[M].哈尔滨:哈尔滨工程大学出版社,1998.
[3]史忠植.神经网络[M].北京:高等教育出版社,2009.
[4]Fredric M.Ham,Ivica Kostanic.神经计算原理[M].叶世伟,王海娟译.北京:机械工业出版社,2007.
[5]张晓安,杨庆.高校科研能力与科研持续发展[J].中国科技论坛,2003,(6).
[6]宋涛,唐德善,曲炜.基于离散型Hopfield神经网络的项目风险分析模型[J].统计与决策,2005,(3).
责任编辑:张洪洋
G472.5
A
1009-1890(2010)03-0065-04
2010-07-19
何黎(1986-),女,湖北武汉人,武汉科技大学管理学院技术经济与管理专业风险管理专业硕士研究生。
