系统噪声对挠性卫星姿态控制稳定性能的影响*

2010-11-07谈树萍雷拥军

空间控制技术与应用 2010年1期

谈树萍，雷拥军，汤亮

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190)

挠性卫星姿态快速机动模式主要用来实现对地面不同目标的观测、对地面同一目标的立体观测和对空间目标的跟踪.在姿态快速机动模式中要求在尽可能短的时间内完成从一个姿态向另外一个姿态的机动控制.为了满足有效载荷的工作需求，往往要求复杂卫星在快速机动后能够快速稳定[1-3].

针对具有高精度控制、大尺寸大柔性附件、多贮箱、大充液量、复杂多体运动的卫星，快速机动与快速稳定在复杂卫星控制中相互制约，相互牵连，其难点主要来源于两个方面：非线性不确定系统的动态与稳态性能指标的影响分析和达到综合指标的控制器动态规划.目前关于控制器动态规划的相关文献很多，例如文献[4]提出了一种基于非约束模态方程的方波序列控制方法，并给出了最小机动时间的方波规划方法.复杂卫星的快速机动与快速稳定总体性能指标的影响因素众多，如复杂卫星的挠性部件、推进燃料、测量部件、执行部件等.但是目前为止，关于复杂卫星在快速机动后快速稳定过程中的稳态性能指标的影响分析工作还很少，尤其是缺乏测量随机噪声和力矩随机噪声对卫星稳态性能影响方面的分析工作.

本文针对挠性卫星和中心刚体卫星，对存在随机噪声情况下，挠性附件对卫星姿态指向精度和稳态性能的影响进行了分析.根据分析结果，挠性部分对卫星姿态指向精度和稳定度的影响主要体现在帆板模态频率和快速机动后模态位移初值上.当存在测量噪声和力矩噪声时，挠性附件降低了卫星的指向精度和稳态性能.

1 带有太阳帆板的复杂卫星动力学模型

1.1 挠性卫星的动力学模型

本文针对典型的挠性卫星给出其结构示意图[5](见图1)和动力学方程.设OBxByBzB为卫星本体坐标系，ONxSGNySGNzSGN、OSxSGSySGSzSGS分别为北、南帆板坐标系，当帆板转角αp=0时，xB的方向与帆板平面垂直.

图1 由中心刚体和南北两翼太阳帆板构成的卫星

姿态动力学方程为

(1)

(2)

(3)

本文暂不考虑帆板转角测量噪声及SADA步进力矩噪声，假设帆板转角αp=0.做变量代换，令

x1=ηl,x2=ηr,

(4)

并记

其中Im×m表示m阶的单位矩阵，则方程(1)～(4)可写为

经过简单的运算，可得

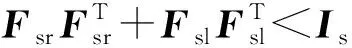
(5)

引理1[6].对于适当维数的矩阵A、B、C、D，在假定有关矩阵可逆的情形下，有

(6)

根据式(5)～(6)，卫星姿态角速度和挠性模态位移及其一阶导数满足

(7)

(8)

1.2 测量噪声和力矩噪声建模

假设φN、θN、ψN和φ1,N、θ1,N、ψ1,N分别是t时刻的姿态角测量噪声和姿态角速度测量噪声，τc为力矩噪声，且姿态角测量噪声、姿态角速度测量噪声和力矩噪声两两独立.定义φN、θN、ψN、φ1,N、θ1,N、ψ1,N和τc为如下的布朗运动的微商：

其中D1(t)、D2(t)、D3(t)分别为3维列向量，且测量噪声和力矩噪声的期望值和方差满足

EΦN=0,EΦ1,N=0,Eτc=0,

2 控制器设计

令Kp=a1Is,Kd=a2Is.卫星受到的所有外力矩Ts由控制力矩Tc和外扰动力矩Td共同构成，即

Ts=Tc+Td

(9)

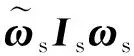
对小角度机动，卫星相对于惯性空间的角速度在本体坐标系下有关系式

dYt=AYtdt+Tδdt+DdWt,

其中，

根据随机噪声的定义，W为标准布朗运动，满足

EW=0, E(WWT) =tI.

3 系统噪声对挠性卫星姿态控制稳态性能的影响

不考虑外干扰力矩的随机性，则Yt期望值为

(10)

Yt的方差为

σ2(Yt) =E((Yt-EYt)(Yt-EYt)T)

(11)

其中σ2(Y0) =E((Y0-EY0)(Y0-EY0)T)，表示考虑挠性附件情况下系统初值的方差.

显然，根据式(10)，当模态位移初值较大且稳定时间较短时，姿态角指向精度指标变差，根据式(11)，姿态稳定度指标由机动后系统初值的方差、状态矩阵A、噪声矩阵D和稳定时间决定，其中状态矩阵A与挠性耦合系数矩阵Fsr、Fsl，卫星转动惯量Is，PD控制器参数相关.

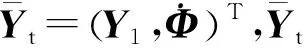
(12)

式中，

根据文献[7]，解式(12)，得

(13)

方差为

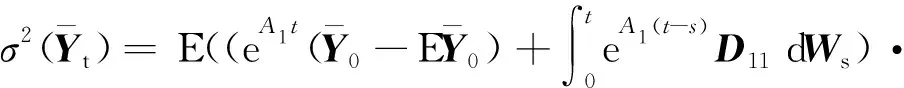
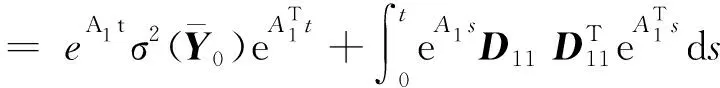
(14)

4 算例

为了对以上结论有更直观的认识，下面给出一个具体的算例.

针对某卫星，假设转动惯量矩阵、控制律系数、干扰矩阵分别为

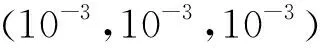
为了简化计算，假设三轴的测量噪声和力矩噪声相同，控制周期为64 ms，D1(t)=(4.8×10-6,4.8×10-6,4.8×10-6)Trad，D2(t)=(1.2×10-6,1.2×10-6,1.2×10-6)Trad/s，D3(t)=(8×10-3,8×10-3,8×10-3)TN·m，并且模态位移初值服从均值为5×10-3，标准差为10-4的正态分布，机动后姿态角偏差的初值服从均值为3.5×10-4rad，标准差为1.2×10-4rad的正态分布，姿态角速度服从均值为10-4rad/s，标准差为10-5rad/s的正态分布.

基于某卫星的挠性参数，可以计算得A、Tδ、D，这里A和D分别为30×30和30×9的矩阵，为了节省篇幅，本文不再详细列出矩阵A和D.当不考虑外干扰Tδ时，如果控制时间为60 s，根据式(10)～(11)姿态角和姿态角速度的期望值分别为

E(Φ-Φm) = (0.2，0.1，1.3)T×10-2(°)，

偏航轴姿态角速度标准差为1×10-4(°)/s.

当视卫星为中心刚体时，同样是机动后采用姿态稳定控制器控制60s后，根据式(13)～(14)姿态角和姿态角速度的期望值分别为

E(Φ-Φm) = (1.3，1.3，1.3)T×10-3(°)，

偏航轴姿态角速度标准差为2.5×10-5(°)/s.

显然，测量噪声、力矩噪声和挠性附件均会降低卫星的指向精度和稳态性能.