挠性卫星PID受控系统特征频率
2010-11-07李丽琼苟兴宇
李丽琼, 苟兴宇
(1.北京控制工程研究所,北京 100190; 2. 空间智能控制技术国家级重点实验室,北京 100190)
相对于刚体卫星,挠性卫星由于带有各种挠性附件,结构变得更加复杂,因此增加了建模和控制等方面的难度.为提高挠性卫星的控制精度,除了在姿态控制算法上进行改进外,还可以采用在轨辨识技术.
在轨辨识是一项新技术,在所能查阅到的国外文献中,最早利用在轨辨识技术的是1989年美国的木星探测器Galileo[1].其控制器设计中采用了陷阱滤波器,而滤波器的设计需要精确知道卫星的关键模态频率,因此引入了在轨辨识技术.
为避免卫星姿态因在轨辨识时的激励而失去基准,最好采用闭环在轨辨识的方式,即辨识时保持控制器工作.此时辨识得到的参数实际上并不是卫星挠性附件的模态参数,而是包括控制器在内的整个受控系统的特征参数,这个值是与控制器参数相关的.
本文以一类挠性卫星为研究对象,提出受控系统的特征频率的概念,着重研究PID控制器参数与受控系统特征频率之间的关系,并通过在传统PID控制系统中引入谐振滤波器的仿真实例说明了受控系统特征频率在在轨辨识中的应用.
1 PID控制器参数与受控系统特征频率的关系
1.1 几类不同的特征频率
挠性卫星的模型可以分为约束模型和整体模型两种,对应的有约束模态频率与非约束模态频率.忽略阻尼项时,非约束模态与约束模态的频率和增益存在确定的关系[2].
若进一步将从设定输入到量测输出之间的包括PID控制器在内的整个卫星受控系统作为一个整体对象来考虑,则根据经验,这个“整体对象”将表现出新的振荡频率,称之为“受控系统特征频率”.受控系统特征频率是有别于约束模态频率和非约束模态频率的另一种频率,它的值与控制器参数有关.
1.2 理论分析
以图1所示的简单受控系统为研究对象.其中,
卫星对象只保留一阶模态频率,将卫星的惯性加速度、太阳帆板的转速、太阳帆板的弹性变形位移等视为小量,并忽略所有角速度非线性项后,得到简化的线性化模型,其约束模型可写为
(1)
式中,ω1和k1分别表示约束模态频率和增益,I是卫星的转动惯量,ξ为阻尼系数.经推导,在忽略阻尼项的情况下,可得到其整体模型如下:
(2)
式中Ω1和K1分别为非约束模态频率和模态增益.

图1 简单PID受控系统框图
PID控制器的传递函数为
(3)
选用式(2)所示的整体模型作为卫星对象的模型,则受控系统的传递函数如式(4)所示.
(4)
令式(4)中的分母N(s)=0,如能解出其特征根,即可得到描述受控系统特征频率与PID控制器参数之间关系的解析式.但是,从式(4)可以看到,N(s)=0是一个五次方程.根据阿贝尔定理,五次方程一般无法求得解析解.因此以下将从数值角度来分析控制器参数与受控系统特征频率间的关系.
首先通过计算体会PID控制参数选为某特定值时受控系统特征频率与约束模态频率、非约束模态频率间的数值差异.取PID控制器参数为Kp=13.235,Kd=92.502,Ki=0.001;卫星的约束模态频率ω1=0.11 Hz,约束模态增益k1=0.018,根据公式可算得非约束模态频率Ω1=0.111 Hz和模态增益;卫星转动惯量I=462.51 kg·m2.将以上参数代入式(4),可得到五个特征根,其分布情况见图2.
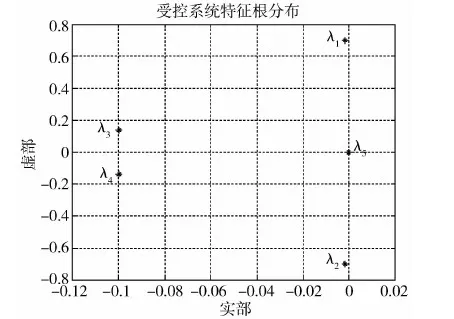
图2 受控系统特征根分布图
从图2可以看出,受控系统在接近原点处有一个负实根,另外有两对共轭复根λ1,2和λ3,4.其中λ1,2离虚轴很近,可认为λ1,2是主导极点.
因而受控系统有两个特征频点,分别对应于特征根λ1,2和λ3,4.基于物理概念可初步做出如下分析:λ1,2的虚部绝对值较大,且所对应的阻尼值较小,因而振荡频率较大且振荡时间较长,相应的频率应该是挠性卫星的非约束模态在受控时表现出来的频率,称之为“受控非约束模态频率”,记为fc1或Ωc1;相应的阻尼称为“受控非约束模态阻尼”,记为ξc1.而λ3,4虚部绝对值较小,且所对应的阻尼值较大,因而振荡频率较小且振荡被较快地衰减,相应的频率则应是卫星的刚性转动自由度在控制器作用下形成的频率,称之为“受控刚体模态频率”,记为fc2或Ωc;相应的阻尼称为“受控刚体模态阻尼”,记为ξc2.
经简单推导得出,无阻尼角频率及阻尼与特征根之间存在如下关系:
(5)

(6)
而阻尼角频率与无阻尼角频率的关系如下:
(7)
根据公式(5)~(7),代入数据计算,可得到非约束模态受控频率值
fc1≐0.110 98 Hz
(8)
与设定的约束模态频率和非约束模态频率值比较,可见受控系统的非约束模态频率值与卫星的非约束模态频率值非常接近.虽然三者有明显的概念区别,但某些情况下三者在数值上很相近.
1.3 仿真研究及分析
下面通过仿真研究PID控制器参数变化时受控系统两个特征频率的变化规律.需说明的是,仿真中发现,某些情况下fc2对应的特征根将由共轭复根蜕变为两个负实根,即阻尼值从欠阻尼变为过阻尼,此情况下,仍旧按式(5)和式(6)计算频率和阻尼值.
(1)Kp与受控系统频率的关系
取Kd=92.502,Ki=0.001,Kp取值区间为[1, 1001],每间隔10取一个值.
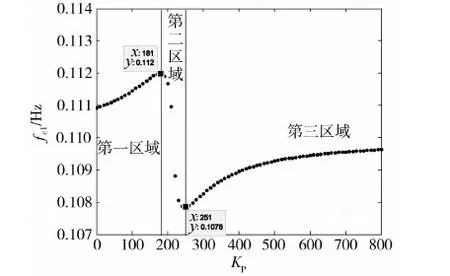
图3 Kp与非约束模态受控频率fc1的关系图
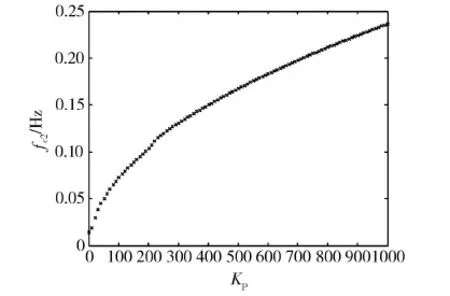
图4 Kp与刚体受控频率fc2的关系图
先考察受控非约束模态频率fc1.从图3和表1可以看出,当Kp增大时,fc1的变化范围不大,基本在(0.110±0.002) Hz的范围内.按fc1变化规律的不同,图3大致可分为三个区域,fc1较大的变化主要出现在第二个区域内.从表1可以看到,在此区域内受控刚体模态频率fc2的值约为0.097 71~0.119 85 Hz,接近fc1的值.这说明,此时受控刚体模态与一阶非约束模态发生了较大的耦合作用,因此导致fc1发生较大变化.以下将第二区域称为耦合区域.
从物理概念上分析,可以将卫星受控系统理解成一个简单弹簧-阻尼器-质量系统,当Kp趋于无限大时,相当于弹簧的刚度趋于无限大,这种情况相当于卫星的中心体被牢牢“卡”住,因而此时非约束模态受控频率趋于卫星帆板的约束模态频率.
再考察刚体受控频率fc2.从图4和表1的结果可以看出,当Kp值增大时,受控系统的刚体受控频率fc2将随之增大.对此可从理论上分析如下:对于简单的单刚体卫星,经推导,其受控系统特征频率(用ωrgd表示)与Kp和Kd存在如下关系:
(9)
由式(9)可见,ωrgd相对于Kp呈抛物线变化趋势(由于ωrgd>0故抛物线只有半支),该结果与仿真结果相符(见图4和表1).
(2)Kd与受控系统频率的关系
取Kp=13.235,Ki=0.001,Kd取值区间为[1,1001],每间隔10取一个值.
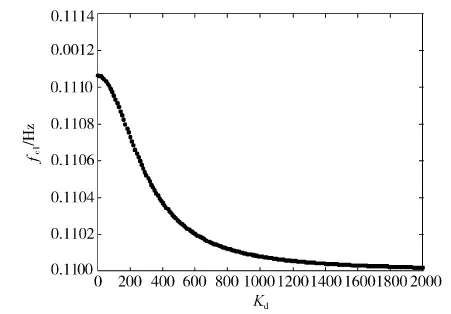
图5 Kd与受控非约束模态频率fc1的关系图
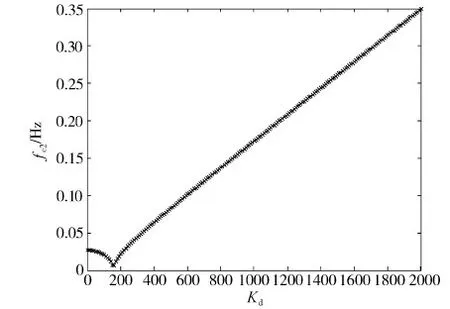
图6 Kd与受控刚体模态频率fc2的关系图
从图5和表2可以看出,当Kd值在较大范围内变化时,非约束模态受控频率fc1的变化范围较小.当Kd值增大时,fc1的值随之单调减小;当Kd值增长到较大值并持续增大时,fc1的值缓慢减小并逐渐逼近频率值0.110 Hz,即卫星的约束模态频率值.
同样可以从物理概念上对上述结果进行分析.将卫星受控系统理解成一个简单弹簧-阻尼器-质量系统,当Kd趋于无限大时,相当于阻尼器的阻尼趋于无限大,这种情况相当于卫星的中心体被牢牢“粘”住,因而此时非约束模态受控频率趋于卫星帆板的约束模态频率.
从图6和表2可见看出,当Kd值增大时,刚体受控频率fc2的值先减小而后增大,图中存在一个转折点,转折点处Kd=161.经分析知,在Kd=161这一特定值处,受控刚体模态阻尼ξc2由小于1变为大于1,即由欠阻尼变为过阻尼.
(3)Ki与受控系统频率的关系
取Kp=13.235,Kd=92.502,Ki取值区间为[0.001,2.501],每间隔0.1取一个值.
从图7可以看出,当Ki变化时,受控非约束模态频率与受控刚体模态频率fc2的变化范围均很小.说明参数Ki对受控系统特征频率的影响很小,可以忽略不计.
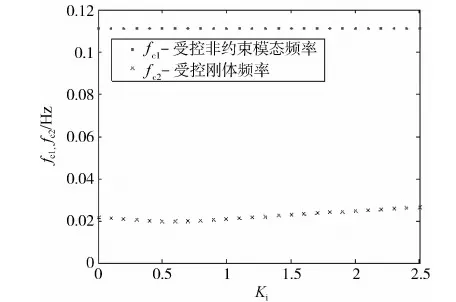
图7 Ki与受控非约束模态频率及受控刚体模态频率的关系图

表1 Kp与受控系统两个频率的关系仿真数据列表

表2 Kd与受控系统两个频率的关系仿真数据列表
综合上述三个仿真可见,PID控制器参数中,对受控系统特征频率有影响的主要是Kp和Kd,而Ki的影响很小,可以忽略.图8给出了Kp和Kd与非约束模态受控频率fc1之间的三维关系图.
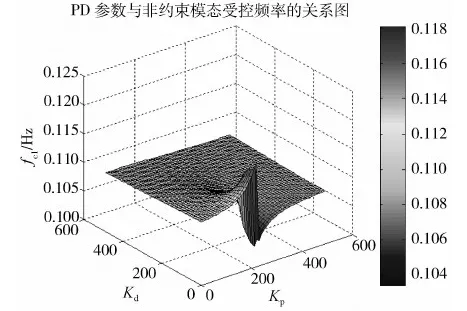
图8 Kp、Kd与受控非约束模态频率fc1的三维图
从三维图可以直观看出PID控制器参数取不同值时所对应的受控非约束模态频率值及其变化趋势.从图8中的色柱可以看到,当Kp和Kd在较大范围内变化时,受控非约束模态频率的变化区间大约为[0.104 Hz, 0.116 Hz],变化范围是比较小的,大部分区域对应的频率值都非常接近0.11 Hz,即卫星的约束模态频率值.当Kp值在如图3所示的耦合区域且Kd值较小时(小于100),受控非约束模态频率fc1的变化幅度相对较大(见图8曲面中凸起的区域).
保留高阶模态后,对应非约束受控频率变化情况与图8类似.
2 受控特征频率在闭环在轨辨识中的应用
仍以1.3节的卫星模型为控制对象,即一阶约束模态频率值为0.11 Hz.PID控制器参数按剪切频率ωc=0.2·2π≐1.256 6 rad/s和相位裕度γ=40°进行设计,取Kp=570.25,Kd=363.14,Ki=0.001.此时受控系统的带宽将包含一阶模态频率点,为兼顾系统带宽和稳定性要求,引入谐振滤波器.
PID控制中引入谐振滤波器后的控制系统示意框图如图9所示.
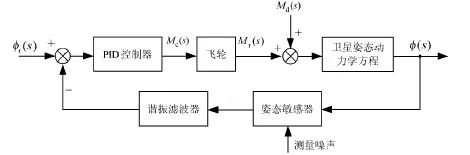
图9 引入谐振滤波器的PID控制系统框图
谐振滤波器的一般形式为[3]
(10)
式中,ωz和ωp分别为滤波器的零、极点频率,由在轨辨识结果确定,通过将谐振滤波器的极点频率设置在特定模态频率附近,加强该频率的负反馈,能够起到抑制振荡的作用.
前面已经提到,受控系统特征频率在轨辨识的结果即为卫星的受控非约束模态频率.根据PID控制器参数的设置,容易计算得到受控非约束模态频率值的理论值,计算结果为:fc=0.110 43 Hz.假设通过在轨辨识准确地得到了该频率值,即取ωz=ωp=2πfc≐0.693 85 rad/s,同时设置ξz=0.1,ξp=0.005,由此得到谐振滤波器的传递函数为
(11)
对引入谐振滤波器的受控系统进行0°到1°阶跃响应仿真,并与不加结构滤波器时的结果进行比较.仿真结果显示,引入谐振滤波器后,姿态角速度由4.396×10-3(°)/s减小为1.557×10-4(°)/s,姿态角偏差如图10所示.
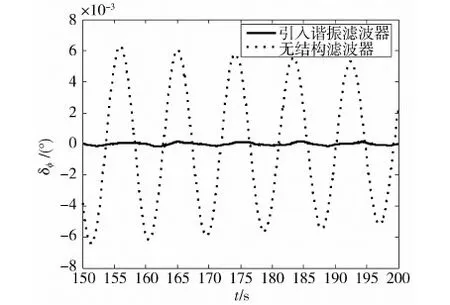
图10 阶跃响应姿态角偏差比较
从以上仿真结果可以看出,在谐振滤波器的作用下,阶跃响应的姿态角偏差大幅度减小,取得了良好的控制效果,同时稳定度得到了提高.
以上结果是在假设在轨辨识能够准确得到受控模态频率值的前提下得到的,而实际中受各种因素影响必然会存在着辨识误差,此时便不能准确地设置谐振滤波器的零极点频率值.下面进行进一步研究,通过仿真观察滤波器的零极点频率设置对滤波效果的影响.
分别将谐振滤波器的零极点频率设置为卫星约束模态频率0.11 Hz附近的不同值,观察最终输出姿态角偏差的变化情况.结果见图11.
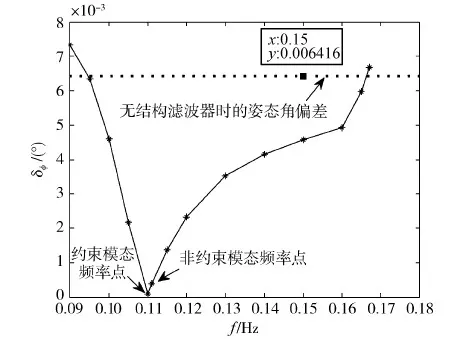
图11 谐振滤波器频率设置与姿态角偏差的关系曲线
从图11可以看出,当谐振滤波器零极点频率设置在卫星约束模态频率点时,可取得最佳的滤波效果;当零极点频率在约束模态频率值附近较大的范围内变化时,都可以得到良好的滤波效果.
3 结 论
本文研究了挠性卫星的两类模态频率及其在受控情况下的特征频率.仅保留一阶挠性模态时,挠性卫星的PID受控系统有两个特征频率,分别为挠性卫星的非约束模态在受控时表现出来的频率fc1(即受控非约束模态频率)以及卫星的刚性转动自由度在控制器作用下形成的频率fc2(即受控刚体频率).仿真结果表明,Kp和Kd的值越大,则fc1越接近卫星的约束模态频率值,从数值仿真及物理概念中,可以预见当Kp和Kd趋于无穷时,fc1将趋于约束模态频率值;刚体模态频率fc2随Kp近似按抛物线形式变化,随Kd的增大近似呈线性趋势增长.Ki对非约束模态受控频率和刚体受控频率几乎没有影响.在保留多阶模态时也有相似结果.
本文最后结合仿真算例研究了受控系统特征频率在在轨辨识中的应用,通过在传统PID控制系统的反馈通道中引入谐振带通滤波器,并以在轨辨识得到的受控系统特征频率设置谐振滤波器参数,能够有效提高控制精度,并且谐振滤波器对参数的设置精度要求相对比较宽松.
