脉冲星导航的整周模糊度解算方法研究*
2010-11-07黄震,李明,帅平
黄 震,李 明,帅 平
(中国空间技术研究院,北京 100094)
X射线脉冲星导航(XPNAV)是一种全新的航天器自主导航方法.它直接探测来自于脉冲星的X射线光子,使在轨航天器可以高精度地自主确定包括位置、速度、姿态和时间在内的全部导航信息.这种导航系统不仅可以为航天器提供10 m量级的自主定轨精度,而且还可以为导航卫星提供外部的时空基准,解决导航星座的整体旋转问题[1],广泛适用于地球卫星、深空探测器和行星着陆器,具有重要的理论研究意义和工程实践价值.
XPNAV导航系统的几何定位原理是:通过测量同一个脉冲信号到达太阳系质心(SSB)和到达航天器所在位置的时间差(TDOA)来确定航天器相对于SSB在脉冲星视方向上的距离,从而估算出航天器在太阳系中的位置平面,若对3颗或3颗以上的脉冲星进行观测,就可以得到一系列可能的位置平面,这些平面的交点就确定了航天器在空间中的真实位置[2].
TDOA可以通过比较脉冲波形的相位差间接提取.但是在航天器上测量得到的脉冲相位只能反映实际相位的小数部分[3],而从航天器到SSB的距离上究竟存在多少个整周期的脉冲信号却无法测量,只能通过数学方法获得脉冲整周数的估计值,这就是脉冲星导航中的整周模糊度解算问题.可以说,整周模糊度的确定直接决定了XPNAV导航系统的所有预报参数的正误.因此本文对基于XPNAV导航的整周模糊度进行了初步探索和研究.首先通过与GPS载波相位模糊度的对比,分析了脉冲星信号整周模糊度的基本特征,然后根据其特点提出了3种可能的模糊度解算方法,最后通过数值仿真分析验证了这些方法的有效性.
1 脉冲相位模糊度的基本特征
脉冲星导航中的整周模糊度解算方法可以借鉴GPS载波相位模糊度解算问题的快速求解方法,但是由于X射线脉冲星辐射信号的特点,两者也存在着不小的差距,具体体现在:
1)作为人造系统,GPS的导航电文中添加了卫星的星历信息和电文播报的时标信息,可以轻易地计算出卫星到接收机天线间的伪距;而X射线脉冲星到太阳系的距离十分遥远,其距离不能精确测定,且没有任何附加信息.
2)任意一颗GPS卫星均在L1和L2个中心频率上播发导航信号,可以通过高精度地测量双频伪距解算出载波的模糊度[4];而X射线脉冲星仅有1个频段的辐射信号.
3)目前每颗GPS卫星的导航电文都在L频段播报,其信号波长比较统一,利于空间划分和搜索;而脉冲星的辐射信号波长完全由脉冲星的自转周期决定,其波长可相差1000倍.
4) GPS载波相位模糊度解算方法中需要考虑多径效应、电离层延迟等影响因素;而在X射线脉冲星导航系统的模糊度解算中,由于接收设备在地球大气层以上,通常只需考虑系统噪声和测量误差的影响.
5) GPS导航电文的波长相对较小,仅为20 cm,一旦发生周跳现象将严重影响导航精度,需要立即通过先进的数学方法进行估算,修复失锁的模糊度参数;而脉冲星辐射信号的波长均在几百公里以上,在通常情况下,即使发生整周计数跳变,航天器仍然可以根据先验的轨道预报信息,正确地估计出所有脉冲星的相位模糊度.
可见,脉冲星导航的整周模糊度在通常情况下并不需要专门求解,但是当电子计数器发生故障、导航系统初始化或处于恢复阶段、深空探测器完全迷失方位等极端情况下,即不能保证当前航天器位置的预测值与真实值相差100 km以内时,才需要进行整周模糊度解算.由于脉冲星辐射信号没有星历、时钟等信息,一般仅能采用空间搜索法进行解算[5].
2 脉冲星整周模糊度解算的一般方法
空间搜索法按搜索空间可以分为在模糊度估值域的搜索和在坐标估值域的搜索两类[6],是解算脉冲星信号整周模糊度问题的首要方法.图1以二维平面为例,描述了在模糊度估值域进行空间搜索的一般方法.图中搜索信号1和搜索信号2的平行线表示所有脉冲相位为测量相位的空间点集,平行线间距表示脉冲信号的一个周期.这些平行线在二维平面内交织成网,其在搜索半径以内的交点组成了模糊度估值域,在这些待测的模糊度估值中,与检测信号的测量相位相符的就是要解算的正确模糊度(TA,true ambiguity).本文采用3种模糊度空间搜索法进行解算,现分别介绍如下.
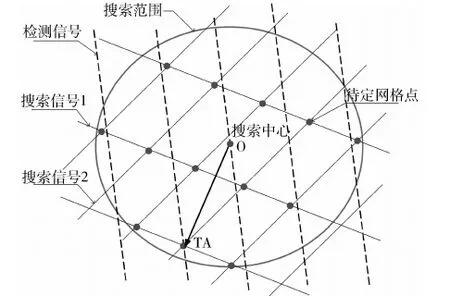
图1 二维平面内的模糊度空间搜索法示意图
2.1 单差搜索法
单差是指航天器在轨观测的脉冲相位与该时刻SSB预报的脉冲相位之差.采用单差搜索法,首先要建立整周模糊度的搜索空间,确定模糊度的估值域.模糊度搜索空间是一个关于中心点对称的三维空间,其中心点的选取应视情况而定.对于计数器故障造成的模糊度跳变,可以选取最近已知的空间位置作为搜索中心;对于导航系统正处于初始化阶段的地球卫星可以选取地球质心为中心点;对于迷失在宇宙中的深空探测器可以选取任意已知点作为模糊度搜索空间的中心.模糊度搜索空间的搜索半径可以选取为航天器所有可能的空间位置与搜索中心之间的最大距离.
利用式(1)可以建立空间搜索范围与模糊度取值范围的对应关系:
(1)
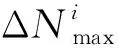
任选3颗导航脉冲星按式(1)进行变换可以得到3个模糊度取值空间,对这些待定模糊度进行组合就形成了待搜索的模糊度估值域.在模糊度估值域中任选1个元素,记作:(ΔN1,ΔN2,ΔN3),则有[7]:
(2)
式中,X是航天器相对于SSB的位置向量,ΔNi为选定的脉冲相位整周模糊度,Δφi为观测相位与SSB预报相位之差.由此可反求出航天器位置的预测值Xe.
将计算得到的预测值Xe代入式(3)统计相位残差,当残差的模大于某临界值(如0.1)时,便将该组模糊度估值从域中剔除.重复该匹配过程,直至域中剩余最后一个元素,就是要求解的相位模糊度.
(3)
式中,函数round(·)表示对变量按四舍五入取整数.
2.2 最小二乘搜索法
最小二乘搜索法的基本思想是,在所有的双差整周模糊度中,只有3个是独立的,即只要能确定3个脉冲相位双差模糊度就可以唯一确定所有的双差模糊度.双差观测量如式(4)所示:
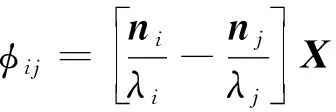
(4)
式中,Δ▽Nij是双差模糊度,Δ▽φij是双差相位.双差观测量实际上是两个单差观测量之差,采用双差模糊度代替单差模糊度可以消除两个观测量之间的公共误差,提高筛选效率.最小二乘搜索法的具体方法可以分为以下3步:
(1)确定模糊度搜索空间
最小二乘搜索法也是在模糊度估值域内的搜索方法,其搜索空间的确定与单差搜索法十分接近.需要注意的是,该模糊度估值域是3个模糊度取值空间的差的组合,即
(5)
(2)最小二乘确定位置估值
由于所有双差模糊度方程中只有3组是独立的,因此在模糊度估值域中的任何一个元素都能唯一确定所有脉冲信号的双差模糊度,称为模糊度预测值.将该组模糊度预测值代入式(4)中可以得到一系列方程,以矩阵的形式表述为:
(6)
式中,A为量测方程的系数矩阵,Z为量测向量.则对航天器位置的预测值Xe可以根据最小二乘准则得到:
Xe=(ATA)-1ATZ
(7)
(3)固定整周模糊度
将利用最小二乘法得到的位置预测值Xe代入方程(4)中,计算出每个脉冲信号的相位残差向量V,其方差因子可以写成矩阵的形式[4]:
(8)
式中,C为双差相位观测量的协方差阵,n为脉冲相位双差观测值的个数.若σ2小于某一限值,则保存该组模糊度估值和σ2,重复(2)、(3)步,直到所有模糊度估值对应的方差因子σ2均小于该定值为止.
此时,模糊度估值域中若仅剩余一个元素,则该模糊度估值即为正确的整周模糊度.否则对所有保存的σ2进行检验,令
(9)
式中,下脚标sub min表示次小值,min表示最小值.若Ratio>2,则认为σ2最小值所对应的整周模糊度估值为正确的整周模糊度.
2.3 模糊度函数法
模糊度函数法是在坐标估值域内的空间搜索法,它首先将整个搜索空间划分成均匀的密集的网格,然后比较每个网格中心点的脉冲相位与测量相位的差异,剔除差异大的格点,直至搜索到正确的坐标.利用模糊度函数的解算步骤如下:
(1)确定坐标估值域
首先按照与模糊度估值域搜索法相同的方法确定搜索空间中心O和搜索半径R,然后以首颗观测脉冲星信号波长的1/10为边长,将整个空间划分成大量的小立方体,每个小立方体的中心代表一个坐标估计值.
(2)网格细化搜索
脉冲星导航的模糊度函数可以定义为:
A(x,y,z)=exp(2πi[Δφ(Xr)-Δφ(X)])
(10)
式中,(x,y,z)表示待检测点的三维坐标,Xr和X分别表示航天器和网格点相对于太阳系质心的位置向量,Δφ(·)表示该位置的脉冲相位,其中Δφ(Xr)由星载X射线探测器直接测量,通过微弱信号处理技术直接获得;Δφ(X)可以通过式(11)进行估算.
ΔN+Δφ(X)
(11)
式中,D0表示脉冲星到太阳质心的距离,b表示SSB相对于太阳质心的位置向量,μ表示太阳引力常数.为计算方便,仿真忽略了SSB和地球质心的位置误差.
对坐标估值域进行网格细化,首先将第(1)步产生的所有坐标估计值代入式(10)中,若A(x,y,z)>0.855,则表示真实位置可能在以该坐标估值为中心以0.1λ为边长的立方体内,保存该坐标估值;然后将通过第一轮筛选后剩余的所有立方体细化为1000个以0.01λ为边长的小立方体,同时对坐标估值域进行更新;最后将所有小立方体的中心点作为坐标估值再次代入式(10)中进行第二轮筛选,若模糊度函A(x,y,z)>0.998,则保留该坐标估计值.
(3)确定整周期模糊度的解
完成第(2)步以后,若坐标估值域中仅剩余1个元素,则该元素即为模糊度的解.若仍存在多个网格点,则需要判断这些点是否集中在半径为100 km的球内,若所有格点聚集成团,则说明航天器位置的真实值就在这个小区域内,可以用它们的均值作为位置的估计值,解算所有脉冲信号的模糊度;若格点不集中,则说明观测数据不足,还需要增加下一历元的观测数据.
值得注意的是,历元更新后,所有的坐标估计值都需要做相应的位置推移.另外由于脉冲星波长差异很大,每次转换观测目标都需要将待定的搜索空间按新信号波长的1/100重新划分网格点,并对坐标估值域进行相应地更新.
3 仿真计算
本文选取了10颗典型的导航脉冲星进行仿真计算[8-9],其数据如表1所示.

表1 脉冲星数据表
假定情景为:地球卫星因故障而完全迷失,导航系统重启后进行初始化,需要重新解算其位置的模糊度.因此,仿真系统将搜索中心定为地球的质心,搜索半径为4万公里,设此时航天器真实的运行轨道为:长半轴a=26 578 100 m,偏心率e=0.001,倾角i=65°,升交点赤经Ω=120°,近地点幅角ω=30°,过近地点时刻τ=0.测量相位信息由航天器真实位置和TOA转换模型[10]计算生成.一般认为要获取来自X射线脉冲星的脉冲信号轮廓需要500 s以上的积分时间,因此本文的仿真计算步长设定为500 s.
3.1 模糊度估值域搜索法
单差搜索法和最小二乘搜索法都属于模糊度估值搜索法,其性能如表2所示.表中模糊度搜索空间表示初始时刻模糊度估值域的大小,正确率指用最终确定的模糊度估值推算表1中列举的所有脉冲星的相位模糊度的正确率.从表中可以看出,这两种方法的解算正确率都是100%,均可以满足模糊度在轨解算的需求.
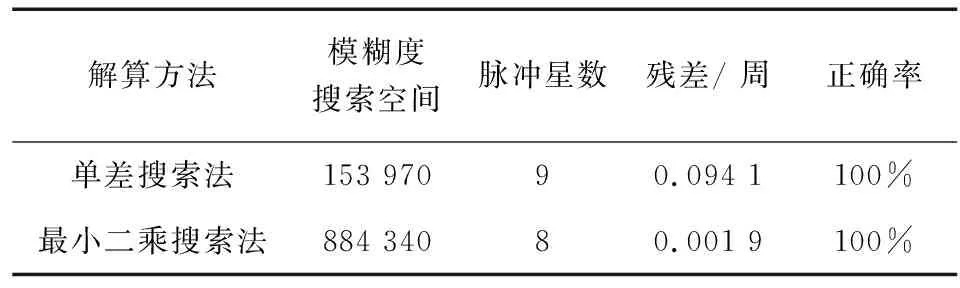
表2 模糊度估值域搜索法比较
虽然单差搜索法的模糊度搜索空间远小于最小二乘搜索法,但是由于最小二乘搜索法采用了Ratio判据,减少了系统的迭代次数,使得二者的总体运算次数在同一量级.同时,最小二乘搜索法采用了双差相位观测量,削弱了观测量共同误差的影响,所以可以利用更少的脉冲星数据正确地计算出相位模糊度.另一方面,该方法采用了最小二乘法推算航天器位置预测值,比单差搜索法利用3个方程直接求解得到的预测值更加接近于真实值,因此大幅度缩小了残差,提高了该搜索方法的准确度和稳定性.
比较式(11)、式(2)和式(4)可以发现,式(2)和式(4)是航天器位置与相位关系的简化形式,所以在仿真中用式(2)和式(4)计算得到的相位预测值与用式(11)计算的“真值”相比,存在10%左右的偏差.仿真试验表明,引入10%左右的相位偏差,并不会影响模糊度参数确定的正确率,但却需要额外多增加2~3颗脉冲星的观测数据.
3.2 坐标估值域搜索法
设仿真过程中速度误差为: [0.5 m/s, 0.5 m/s, 0.5 m/s]T,则采用模糊度函数法的仿真系统利用了7颗脉冲星的相位观测量正确地搜索出了所有脉冲相位的整周模糊度,其相位残差仅为0.00115周,可以用于航天器的模糊度解算.但是,模糊度函数法作为坐标估值域搜索法的一种,其运算量远大于模糊度估值域搜索法,详见表3.
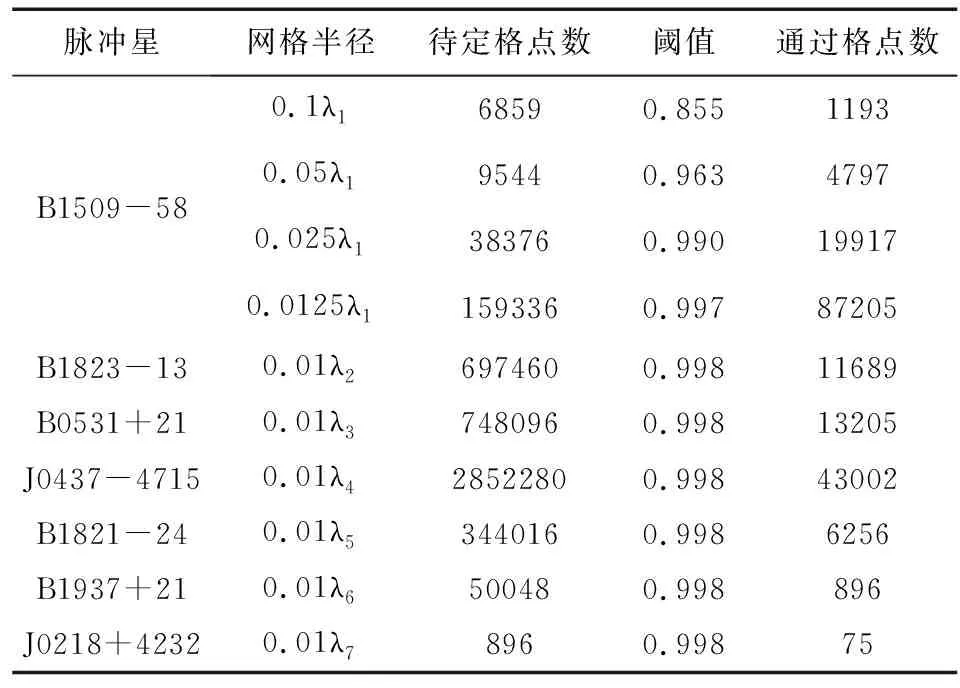
表3 模糊度函数法搜索范围
特别是由于脉冲星的波长差距很大,每次更换观测目标都需要对尚未排除的搜索空间进行重新划分,这种重复的空间划分将不可避免地产生搜索空间重叠的情况,耗费了大量的计算资源,需要进一步的研究加以改进.
为了减少计算量,仿真中采用了逐步细化的方法分4次将空间细分成边长为0.0125λ的立方体集合,并按照波长递减的方式选取检测脉冲星,避免了由于检测点增长过快造成内存不足的缺陷.
另外,利用模糊度函数法通常需要一个以上历元的观测数据,要对坐标估值域中的所有的空间格点进行运动学推算,计算耗时长.但是,这种方法却不需要同时观测3颗以上的脉冲星,可以在单位历元内仅观测1颗脉冲星的相位数据,综合多个历元完成模糊度的解算,适用于装配单X射线探测器的脉冲星导航系统.
进一步的仿真计算表明,在这3种算法中添加1%的相位误差,1′的脉冲星视方向偏差,以及5%的测量误差对模糊度的求解均不能造成明显的影响.这是因为脉冲星信号的波长很长,即使求解过程中对位置的估计有所偏差,也不会导致模糊度求解失败.
4 结 论
装有X射线脉冲星导航系统的航天器在绝大多数情况下,并不需要进行模糊度解算.但是当导航系统初始化、航天器迷失方位等极端情况发生时,仍然需要准确确定脉冲相位的模糊度参数,其解算方法可以采用单差搜索法、最小二乘搜索法和模糊度函数法.最小二乘搜索法在计算残差、量测信息需求等方面明显优于单差搜索法,但是至少需要同时观测4颗脉冲星才能确定模糊度估值域.模糊度函数法的计算量大、计算时间长,但可以通过状态估计综合处理多个历元的观测数据,解决了装配单探测器的X射线脉冲星导航系统无法解算相位模糊度的难题.
下一步工作可以考虑用LAMBDA法、遗传算法等先进的优化方法解算脉冲相位的整周期模糊度,进一步减小模糊度解算方法的搜索空间,提高算法的搜索效率,并结合多普勒测速法,对星载时钟存在钟差等复杂情况进行分析研究.
