一种空间交会绕飞段的小推力滑移制导方法

刘鲁华，郑 伟，汤国建

(国防科技大学航天与材料工程学院，长沙 410073)

空间自主交会技术是未来空间应用的一项关键技术，倍受各航天大国的青睐.近年来，美国已经对DART和OE[1]等自主交会飞行器进行了演示验证试验.从空间自主交会技术的发展趋势看，空间交会技术已经从理论研究进入了实际应用阶段，未来的空间交会技术将成为航天器的一项经常性空间操作，包括空间在轨服务、空间侦查与监视、空间编队飞行等[1]，这些任务中追踪航天器常常需要对目标飞行器或目标区域执行绕飞机动，随着航天器在轨服务任务的多样化，绕飞控制技术将从简单控制走向复杂控制，从特殊形式绕飞走向任意平面绕飞，新的绕飞任务对空间绕飞技术的需求越来越紧迫.另外，随着航天任务对在轨寿命、运营成本和可靠性要求的不断提高，具有体积小、比冲高、成本低廉的小推力推进系统已成为绕飞应用的一种趋势，这种推进系统在小卫星任务中已得到应用，也进一步拓展了绕飞技术的应用范围.

在空间交会任务对绕飞技术强劲需求的背景下，本文研究了一种采用滑移制导实现绕飞机动的方法.滑移制导方法最早用于航天飞机近程交会任务中[2-3]，在考虑导航误差的情况下，文献[4]研究了滑移轨道制导方法在接近、撤离、绕飞和停靠等操作中的应用，文献[5]在前述文献研究的基础上，提出了用于滑移轨道设计的微分方程法和待定系数法，并给出了快速滑移轨道和慢速滑移轨道的概念，文献[6]研究了最优滑移制导方法.这些方法在近程交会轨道操作中具有重要的实用价值，本文进一步研究采用这种方法如何实现绕飞任务的问题.

1 滑移制导在绕飞任务中的应用

1.1 滑移制导基本原理

rm=rT+ρ(tm)ρ°,tm=mT/n,

m=0,…,n-1

(1)

滑移轨道的主要设计内容即确定ρ(t)的变化规律，当ρ(t)确定后，相对运动状态参数即可确定.如果在交会过程中执行靠拢与撤离段操作，则可以直接设计ρ(t)的变化规律.但在绕飞阶段，由于相对距离变化律不具有单调递增或者单调递减的性质，而是在空间形成一个接近封闭的几何构形，其特点不同于靠拢与撤离操作.以下从滑移制导方法的思想出发，分别基于冲量制导和有限推力制导建立空间任意平面的绕飞制导律.

1.2 绕飞约束轨道下的滑移制导

针对近圆轨道绕飞问题，定义目标轨道坐标系O-xyz：原点取为目标飞行器质心，z轴方向为目标质心与地心连线方向，朝向地心为正，x轴垂直于z轴，沿速度方向为正，y轴服从右手法则.以五次机动的绕飞任务为例，在xz坐标面内分圆形绕飞与椭圆形绕飞两种情况，如图 1、图 2所示，其中t1到t5点对应按冲量变轨时每次变轨机动的时刻，圆与椭圆则表示滑移制导方法中的约束轨道，虚线为采用冲量变轨条件下的绕飞轨迹，带端点的实线表示有限推力条件下发动机开机时刻和发动机关机时刻，表示发动机工作的整个过程.由图可见，滑移制导通过一个滑移轨道(即约束轨道)实现对飞行器的绕飞控制，这种方法具有计算简单、控制容易的特点.另外，由于时间T可预先给定，在紧急条件下利用滑移制导方法可以实现快速绕飞控制.

图1 圆绕飞过程示意图

图2 椭圆绕飞过程示意图

以xz轨道平面内的绕飞为例，可以按相位角确定每次机动的位置，假设机动n次，则每次机动的位置为

θym=θy0+2πm/n

(2)

(3)

式中,Δt为机动时间，φ为状态转移矩阵，定义如下：

其中s=sin(ωt)，c=cos(ωt)，ω为目标轨道角速率.

2 空间绕飞滑移制导方法

将坐标平面内的绕飞推广到任意空间绕飞，采用O-xyz坐标描述具有一定的局限性，需要引入一个参考坐标系，将O-xyz绕z轴和绕x轴分别转过两个角度θz、θx形成一个新的坐标系，并将此坐标系定义为参考坐标系O-xryrzr，如图 3所示.

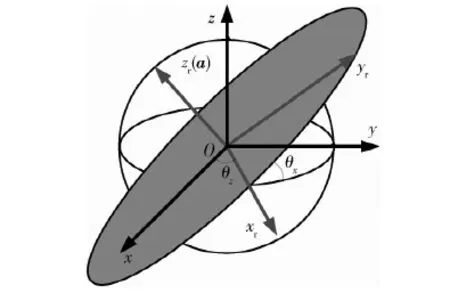
图3 O-xyz与O-xryrzr的关系

坐标系O-xryrzr与O-xyz之间的转换关系为

(4)

式中，Mx(θx)、Mz(θz)分别为绕x轴和z轴旋转θx和θz的单位转换阵，如给定轨道坐标系中的初始位置(x0,y0,z0)，则在参考坐标系中的描述为

(5)

为了描述任意绕飞轨道，引入约束轨道的法向量概念，定义约束轨道法向量为a，利用式(4)可得a在O-xyz坐标系中表示为

(6)

于是有

(7)

y0cosθzcosθx+z0sinθz-x0cosθzsinθx=0

(8)

在参考坐标系中令每次机动时间间隔一定，可定义每次机动对应的相位角为

(9)

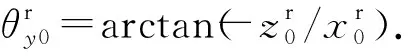
2.1 圆轨道绕飞

针对任意平面内的圆轨道绕飞，则有如下关系成立：

(10)

式中rc为圆轨道绕飞半径，将式(10)转换到O-xyz坐标系中，则有

(11)

2.2 椭圆轨道绕飞

针对任意平面内的椭圆轨道绕飞，则有如下关系成立：

(12)

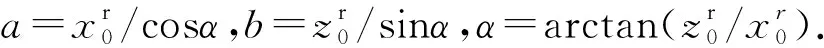
(13)

3 仿真算例

3.1 冲量制导绕飞轨道的实现

给出如表1所示4组绕飞条件，条件1～3为特殊平面绕飞，条件4为任意平面绕飞，则可得如图4所示仿真结果，可以实现任意平面的绕飞操作.

表1 绕飞条件定义

3.2 小推力绕飞轨道的实现

设绕飞飞行器质量为1 000 kg，小推力发动机各方向产生的推力为0.5 N，采用8次机动实现xz平面内的绕飞.若采用开环制导，直接按冲量结果进行小推力绕飞控制会造成较大的偏差，位置误差约为30 m，故需要在绕飞过程中实时进行误差反馈，如果误差超出预期值，则需要进行重新计算，实现一种闭路制导.在工程应用中可以定义一个最大误差球，当绕飞轨道超出误差球，重新进行一次制导计算，以修正累积误差.采用闭路制导可以将误差控制在一定范围内，本算例选择误差球半径为10 m，在此约束下在轨道机动过程中进行了一次修正，控制效果如图5所示.

图4 任意平面内的绕飞控制

图5 有限推力绕飞控制

4 结 论

滑移制导方法可以满足不同周期的绕飞控制任务的要求，此制导方法计算简单，对控制系统要求较低，如果采用闭路制导，可以将制导精度控制在要求的范围内.本方法能够实现任意平面的绕飞控制，可应用于空间营救、安装、维护、监视等在轨任务中去.