动态情况下星敏感器探测灵敏度研究

李 晓，赵 宏，卢 欣

(1.北京控制工程研究所，北京 100190；2.中国空间技术研究院，北京 100094)

星敏感器的探测灵敏度是指星敏感器能够探测到的最弱星等的能力，探测灵敏度的高低决定了视场内恒星的数量.在动态情况下，星像在像平面不断移动，与静态情况相比，星光产生的有效信号电荷分散到更多像元，从而降低了星敏感器的探测灵敏度.

本文以从噪声中检测信号的理论为基础，通过分析像元输出模型，得出单个像元被探测到的条件；进而通过研究星像提取方法和动态情况下星像能量分布特性，推出星像被提取的条件；最后以给定的星敏感器参数为例进行计算和分析.

1 动态情况下星像能量分布特征

在静态情况下，星像能量满足正态分布，点扩散函数可以用二维高斯函数来表示[1]：

(1)

式中， (xc，yc)表示星像中心的实际位置，σPSF为高斯半径，表示点扩散函数的能量集中度.

动态情况下，由于在曝光期间星像中心一直在移动，星像能量分布可以用如下函数表示：

(2)

式中，Te为曝光时间，xc(t)和yc(t)为时刻t(0≤t≤Te)的星像中心位置坐标.考虑到星体角速度一般不大于2(°)/s，曝光时间不大于0.5s，星像中心轨迹很短且近似为直线，因此近似认为xc(t)和yc(t)是线性函数.设星像中心轨迹为线段L，其参数方程为：

(3)

式中，u为星像中心移动速率，θ为轨迹与x轴夹角.设l为轨迹L的长度，l=uTe.将式(3)代入式(2)，并令积分变量t=τ/u得出星像能量分布函数：

(4)

可以看出，在高斯半径一定的情况下，星像能量分布函数只与初始位置(x0，y0)、轨迹L的长度l和轨迹与x轴的夹角θ有关.

2 星像的提取方法

星像的提取通常需要经过两步：

(1)图像的半阈值化

采用全局阈值的方法对图像进行阈值分割，目的是将含有有效信号的像元检测出来，从而确定星像所处区域.阈值由实时得到的图像数据计算获得：

Gth=E+αδ

(5)

式中，E为整幅图像所有像元的灰度均值，δ为整幅图像灰度的标准差，α可根据需要设定.半阈值化函数如下：

(6)

(2)连通域分析

对半阈值化后的图像IT(x，y)进行连通域提取，并通过判断连通域中的像元数目剔除孤立噪声点，获得星像区域.一般要求连通域中的像元数目不小于4，小于4的连通域被认为是孤立噪声点予以剔除.因此星像被提取的条件是，星像区域中大于阈值的像元能形成一定面积的连通域.

3 含有效信号的像元探测

3.1 像元输出模型

星敏感器像元噪声有多种，为简化分析过程，只考虑暗电流噪声、光子散粒噪声、读出噪声、背景噪声和量化噪声，而将其它噪声一并归入读出噪声进行分析.

像元产生的电荷数可用如下的随机变量来表示[2]：

N=Ns+Ndark+B+Nron

(7)

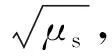
(8)

设像元输出灰度I与像元产生的电荷数N满足如下正比关系：

(9)

m为比例系数，n为量化位数，Nsatu为饱和光电子数.量化过程中会产生服从0～1均匀分布的量化误差，其方差为1/12.所以像元输出灰度I的均值E(I)和标准差为：

(10)

设σquan为量化噪声的等效电荷数：

(11)

则像元输出灰度I的均值E(I)和标准差为：

(12)

恒星在曝光时间Te内产生的总信号电荷数μ0为：

(13)

式中，E0(λ)为零等星λ波段的辐照度，M为星等，D为镜头口径，Eph为单个光子能量，QE(λ)和τ0(λ)分别为λ波段的量子效率和光学系统透过率，Kfill为填充系数.像元产生的有效信号电荷μs可根据总信号电荷数和星像能量分布函数确定.

暗电流μdark可以按如下公式计算：

μdark=JdarkSTe/q

(14)

式中，Jdark为暗电流密度，S为像元面积，q为一个电荷所带电量；背景噪声μB相当于10等星产生的电荷数，读出噪声σron和量化噪声σquan为常数，可根据星敏感器的参数获得.

3.2 含有效信号的像元探测

图像半阈值化的目的是将含有效信号的像元提取出来.根据从噪声中检测信号的理论，从噪声中提取目标像元存在两个指标：一是将目标像元有效提取的概率称为探测率PDET；二是将非目标像元判断为目标像元的概率称为虚警率PFA.理想的探测系统应当使探测概率达到最大，虚警概率达到最小，但两者不可能同时达到最佳，能做到的只是保证虚警概率为某个许可值时，而使相应的探测概率尽可能大[4].

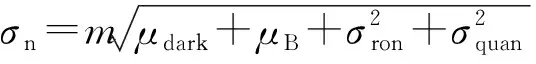
(15)

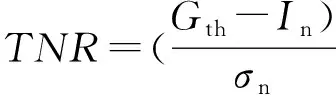
(16)

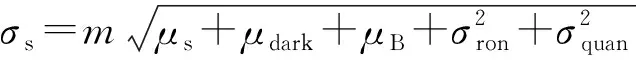
(17)

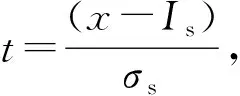
(18)

式中积分上限L为：

(19)

当给定虚警概率PFA和探测概率PDET指标时，通过查正态分布表，可以获得PFA对应的TNR值和PDET要求的最高积分上限Lm.定义像元的信噪差比SNDR为：

SNDR=-L

(20)

则像元满足探测概率的条件为：

SNDR≥-Lm

(21)

根据TNR的定义，理论阈值Gth=TNR·σn+In，由于实际图像处理过程中无法获得σn的精确值，可以用实时图像的样本均值和标准差作为其真值的估计，即E≈In,δ≈σn.故式(5)中系数α等于阈值噪声比TNR.

4 动态情况下星敏感器探测灵敏度

4.1 星像被提取的条件

由星像的提取方法可知，星像能够被提取的条件是：灰度大于域值的像元能形成一定面积的连通域.为便于分析，将星像轨迹区域的像元进行分类，如图1所示.图中斜线为星像中心轨迹L，根据L的走向确定星像区域像元的分类方式，若L的行跨度比列跨度大，则选择按行分类方式，反之选择按列分类方式.当选择按行(列)分类方式时，在每一行(列)像元当中，含有有效信号电荷最多的像元定义为p像元，含有有效信号电荷仅少于p像元的定义为w-1像元，依次类推定义w-2像元、w-3像元……w-n像元.

在同一星像轨迹中，不同的w-1像元所含有的有效信号电荷不尽相同，将其中含有有效信号最少的像元定义为w-1m像元.若w-1m像元满足探测条件SNDR≥-Lm，所有w-1像元和p像元显然满足探测条件，经过图像半域值化，p像元和w-1像元可以形成一定面积的连通域，星像就能够被提取.因此星像能够被提取的条件为：w-1m像元满足探测条件SNDR≥-Lm.

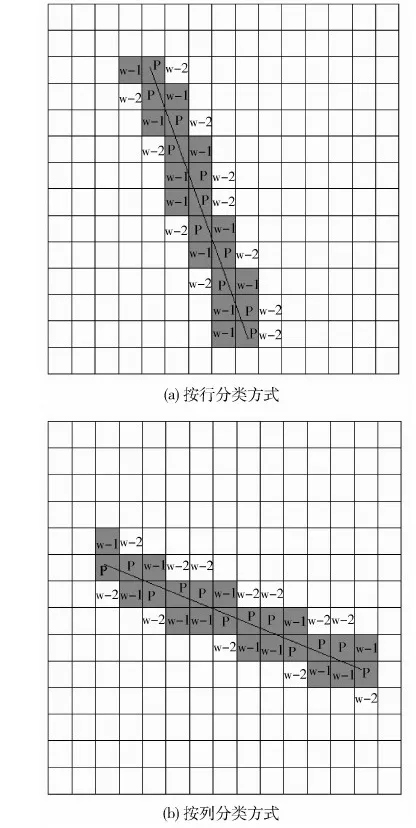
图1 像元分类示意图

4.2 星敏感器的探测灵敏度计算

星敏感器的探测灵敏度是指星敏感器能够探测到的最弱的星的能力.星等越大，产生的有效信号电荷μ0越小，相应的w-1m像元越不易被探测，星像越不易被提取.

设η为w-1m像元生成的信号电荷μsw-1m占总信号电荷μ0的比例：

∬Asw-1mg(x,y)dxdy

(22)

式中，Asw-1m为w-1m像元所在区域；g(x，y)为信号电荷分布函数，只与星像中心轨迹L的长度l，与x轴夹角θ，初始位置(x0,y0)有关.对于确定的星像中心轨迹，η可以通过数值计算得出，而与总信号电荷μ0无关.

当给定虚警率和探测率指标时，TNR和Lm可获得.由式SNDR≥-Lm可确定μsw-1m的最小值，再根据式(22)可以确定总信号电荷μ0的最小值，最后根据式(14)可确定星等的极限值，即星敏感器的探测灵敏度.

实际情况中，η随l、θ、(x0，y0)的变化而变化，是不定值.因此，为保证求出的极限星等在任何情况下都可以被探测到，η应取最小值进行计算.在l确定的情况下，当θ=0且星像中心轨迹L位于p像元中心线时，调整y0的位置，可使η取得最小值ηmin.因此当给定角速度的模ω，求对应的探测灵敏度时，应令角速度的方向平行于y轴或x轴，求得η的最小值ηmin.

当σPSF=1像元时，通过数值计算可得出不同的l对应的ηmin，如表1所示.

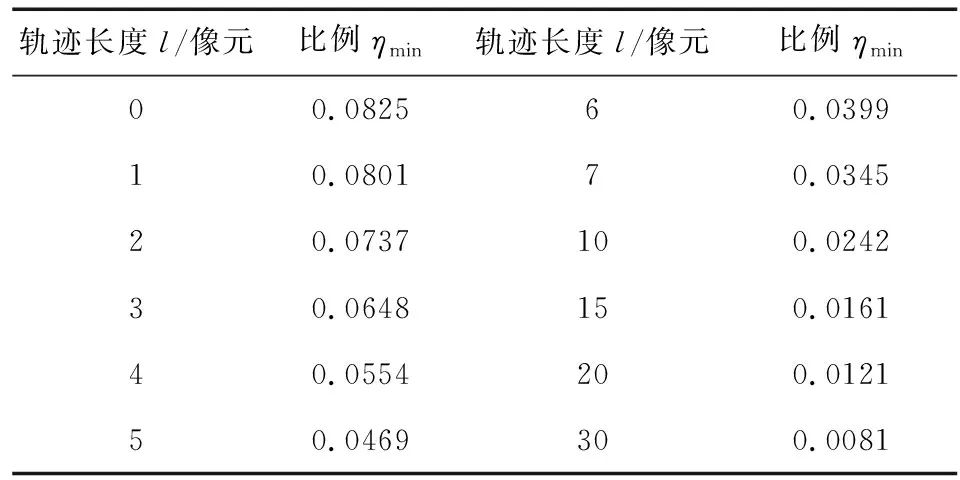
表1 σPSF=1时w-1m像元有效信号占总信号的最小比例ηmin

可以看出，当长度l>5时，ηmin与轨迹长度的乘积近似为定值0.242，因此ηmin近似计算为：

(23)

对于不同的高斯半径，都可以采用数值计算的方法近似得出ηmin与轨迹长度l的关系.轨迹长度l可由式(24)来估算：

l=fωTe

(24)

式中f为焦距，其单位是像元.

4.3 给定星敏感器的探测灵敏度计算实例

表2给定了星敏感器的典型参数，以此为例计算动态情况下星敏感器的探测能力.

图3给出在虚警率PFA=0.01、探测率PDET=0.99，即TNR=2.33、Lm=-2.33时，给定星敏感器在不同的曝光时间下的探测灵敏度.

可以看出，探测灵敏度随角速度增大而减小.同时可以看出，在角速度较小时，曝光时间越长，探测灵敏度越高；而当角速度较大时，增加曝光时间并不能提高星敏感器的探测灵敏度，因为像元接收的信号电荷并没有随着曝光时间的增加而增加，相反暗电流噪声和背景噪声会随曝光时间增加而增加，从而使探测灵敏度略有降低.

表2 给定星敏感器的参数

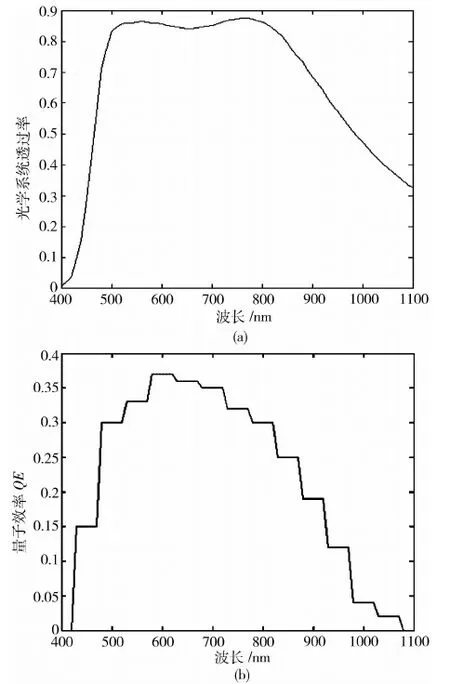
图2 给定星敏感器的光学系统透过率和量子效率

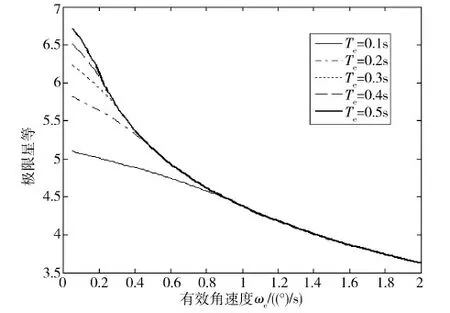
图3 给定星敏感器在不同曝光时间下的探测灵敏度

5 结 论

本文从探测率和虚警率的角度分析了像元能被探测到的条件；并根据像元输出模型和星像提取方法，论证了用w-1m像元的信噪差比来判断星像能否被提取的可行性；最后以给定星敏感器参数计算动态情况下的探测灵敏度，得出在角速度较大时增加曝光时间并不能提高探测灵敏度的结论.