转动惯量未知的非合作目标角速度估计方法研究*

刘智勇，何英姿，刘 涛

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190)

早在20世纪70年代就有人提出了在轨服务型航天器(OOSS，on-orbit servicing spacecraft)的概念，即专门为其他航天器提供在轨燃料补给、仪器设备维修与升级更换服务、轨道与姿态重置等一类机动性较强的航天器.目前，在轨服务已经从概念转化为现实，例如美国利用航天飞机成功地实现了对哈勃望远镜在轨维修，这些实践让人们看到了在轨服务在未来航天技术发展中所具有的重大意义.未来在轨服务任务的对象航天器很多情况下将是非合作目标，研制具备非合作目标在轨服务能力的航天器是目前在轨服务领域的研究方向，各主要航天大国均积极开展了相关研究和在轨试验，如通用轨道修正航天器(SUMO)[1-2]等.

大部分失控和被废弃航天器处于翻滚状态，并且旋转轴指向任意[3].针对这类非合作目标的在轨服务任务中，在轨服务航天器需要利用非合作目标的姿态信息，以保证在轨服务的顺利实施.但是，失控和被废弃航天器的姿态测量系统或是通信设备往往不能正常工作，非合作目标不能提供其姿态信息.从而，在轨服务航天器将配置双目视觉测量系统，测量在轨服务航天器和非合作目标的相对姿态.并且，在轨服务航天器还将配置星敏感器，提供其自身的惯性姿态.联合相对姿态和在轨服务航天器的惯性姿态，可以解算出非合作目标的惯性姿态信息.虽然，在轨服务航天器的姿态角速度可以通过陀螺测得，但是，由于相对姿态角速度不能测量，使得非合作目标的姿态角速度不能直接解算出来，需要进行估计.

非合作目标角速度估计问题，现在国内外研究很少.文献[4]针对利用机械臂对哈勃望远镜在轨维修问题，进行了哈勃望远镜姿态角速度估计算法研究，但是其假定目标转动惯量已知，没有考虑转动惯量不确定性对角速度估计的影响.而由于航天器失效前运行过程中的燃料消耗以及各种复杂环境因素引起的结构变形，非合作目标的转动惯量往往难以了解其准确值.所以，有必要考虑转动惯量不确定性情况下，非合作目标的姿态角速度估计问题.

本文针对转动惯量未知的非合作目标的角速度估计问题进行研究，提出了一种利用解算出来的非合作目标惯性姿态信息，同时对非合作目标的姿态角速度和转动惯量比进行估计的方法.文中利用了微分几何知识，对待估计的状态扩维系统的能观性进行了分析.分析表明，非合作目标的姿态角速度非零是增广系统能观的充分条件.

基于无迹变换(UT)设计的Unscented卡尔曼滤波器(UKF)[5-7]保留了卡尔曼滤波器的递推形式，不需计算Jacobian矩阵，且估计精度较EKF高，非常适合于非线性系统的滤波估计问题.本文在分析了待估计系统的能观性的基础上，利用UKF设计相应的滤波估计算法，估计出非合作目标的姿态角速度和转动惯量比.仿真结果表明，本文所设计的方法能够得到非合作目标姿态角速度和转动惯量比的精确估计.

1 非合作目标运动学及动力学方程

利用姿态四元数描述航天器的姿态[8]

(1)

式中，q为姿态四元数，矢量部分qv和标量部分q4，φ为欧拉转角，e为欧拉转轴.非合作目标的姿态四元数记为qt，定义为从惯性坐标系到目标本体坐标系的转动.在轨服务航天器惯性姿态四元数记为qc.

定义在轨服务航天器和非合作目标的相对姿态为

(2)

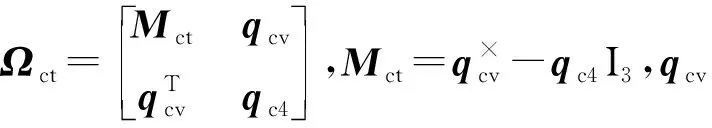
对非合作目标姿态四元数求导，可得其姿态运动学方程

(3)

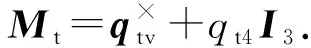
当非合作目标为能料耗尽、系统故障或结构损坏的失效航天器时，由于其不能提供任何主动控制力矩，在空间处于翻滚状态.取非合作目标的主轴惯量坐标系为本体坐标系，主轴惯量分别为J1，J2，J3.在主轴惯量坐标系下，非合作目标的姿态动力学方程

(4)

由于非合作目标的转动惯量为未知常值，所以转动惯量比λt1,λt2,λt3也为未知常数，即

(5)

为了在转动惯量比未知情况下，估计出非合作目标的姿态角速度，现将姿态系统的状态进行扩展，将转动惯量比作为系统状态变量的一部份，即扩维后的系统状态变量为

(6)

根据式(3)～(5)可知扩维后的系统状态方程可记为

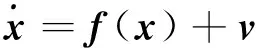
(7)

由于目标是非合作的，目标的惯性姿态、姿态角速度信息未知.为了得到非合作目标的姿态信息，在轨服务航天器将配置星敏感器测量自身的惯性姿态qc，同时还将装配双目视觉测量系统测量非合作目标和在轨服务航天器的相对姿态qe.利用在轨服务航天器惯性姿态qc和相对姿态qe，可以解算出非合作目标的惯性姿态

(8)

将计算得到的非合作目标的惯性姿态作为待估计系统的测量量，故测量方程可以表示为

y=h(x)+w=Cx+w

(9)

2 待估计的扩维系统的能观性分析

定理1.对如式(7)和式(9)所表示的非合作目标姿态系统，系统局部能观的充分条件为非合作目标姿态角速度非零.

证明.

由观测方程式(9)可知

进而有

(10)

(11)

式中,

D13=0.

系统输出的二次李导数为

(12)

式中，*表示不含x8，x9以及x10的多项式.

(13)

下面证明rank(D12)=3.

由于

所以x4≠0时，rank(D12)=3.

当x4=0时，

而

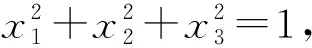
下面对D23的秩进行分析：

由于x5,x6,x7非零，当x4≠0时，rank(D23)=3.

当x4=0时，

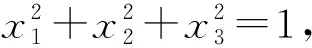
系统能观矩阵为

(14)

从能观性矩阵可以看出，只要

rank(D12)=rank(D23)=3

则能观性矩阵满秩.从上述分析可以看出，只要非合作目标的姿态角速度都不为零，即x5,x6,x7非零，能观性矩阵满秩.根据引理1可得，对于如式(7)和式(9)所表示的非合作目标的扩维姿态系统，当姿态角速度都不为零时，系统为局部能观的.

证毕.

其实，当非合作目标三轴的姿态角速度中有一个为零时，即x5,x6,x7至少有一个为零，系统姿态动力学方程为

(15)

系统状态方程中已无转动惯量比这一参数，非合作目标姿态角速度为常值或零.然而，由于非合作目标受到空间环境力矩的作用，这种状态是不可能长时间存在的.所以，扩维系统的能观性条件实际上是容易满足的.

3 基于UKF的非合作角速度估计滤波算法

采用如文献[4-6]所述的UKF对如式(7)和式(9)所表示的非合作目标姿态系统进行估计滤波算法设计，可得如下UKF算法流程.

(1)一次采样

利用UT变换计算sigma点

(16)

(2)一步预测

(17)

(18)

(19)

(3)二次采样

(20)

(4)测量更新

(yk+1|k)i=h((χk+1|k)i)

(21)

(22)

(23)

(24)

(5)滤波更新

(25)

(26)

(27)

式中，

(28)

(29)

(30)

β用来结合x的分布的先验分布信息，对于高斯分布，β的最优值为2.

4 仿真算例与分析

在完成了如式(7)和式(9)所表示的非合作目标姿态系统的能观性分析和UKF滤波算法设计后，下面将进行相关的数值仿真，验证理论分析的正确性和滤波算法的有效性.

设定非合作目标的转动惯量为Jt=diag{2250,1750,2625}kg/m2，可见惯量比为[0.389 0.214 0.190].转动角速度初值为ωto=[0.04 0.030.06]Trad/s，姿态四元数初值为qto=[0.10350.0518 0.2315 0.9659]T.相应的滤波器估计初值分别为非合作目标姿态四元数为[0.5 0.5 0.5 0.5]T，姿态角速度0rad/s，惯量比0.测量噪声为标准差为0.1°的随机白噪声序列，并且考虑了重力梯度力矩等环境干扰力矩.协方差矩阵的初始值为P0=0.1I10，过程噪声的方差矩阵V=diag{10-12I4，10-10I3，10-12I4}，测量噪声的方差矩阵W=1.6×10-5I4.采样周期为0.02 s.

根据以上设置的估计参数和初始条件进行了数值仿真，仿真结果如下：

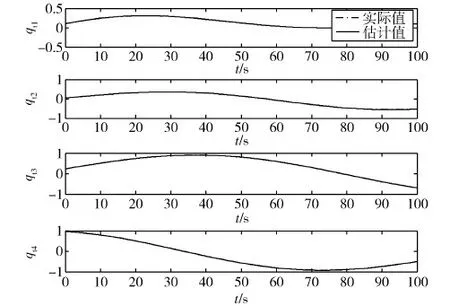
图1 目标姿态四元数和估计值

图2 目标姿态四元数估计误差

图3 目标角速度和估计值

图4 目标角速度估计误差

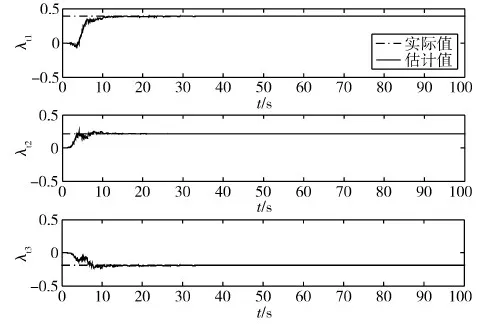
图5 转动惯量比和估计值

图6 转动惯量比估计误差

由图1～4的非合作目标姿态四元数和姿态角速度的参数估计可以看出在10 s内实现估计，姿态角估计精度为0.02°，姿态角速度估计精度为0.003(°)/s；由图5和图6的非合作目标转动惯量比估计参数可以在10 s内实现估计，估计精度为0.003.以上仿真表明，实现了对非合作目标的角速度和转动惯量比的精确估计.证明了文中能观性分析的正确性和基于UKF非合作目标状态估计算法的有效性.

5 结 论

针对转动惯量未知的非合作目标，通过将计算得到的非合作目标惯性姿态作为观测量，将姿态角速度和转动惯量比作为扩维系统的状态，利用UKF设计相应的滤波器，估计得到了非合作目标的姿态角速度和转动惯量比.文中以定理1的形式给出了所设计的姿态确定系统满足局部能观性的充分条件，并指出该充分条件在实际系统是容易得到满足的.仿真结果表明，本文所提出的方法在非合作目标转动惯量未知的情况下，能够精确估计出非合作目标的姿态角速度和转动惯量比.