基于准滑模控制的空间拦截末制导律设计

王国梁，郑建华

(1.中国科学院空间科学与应用研究中心,北京 100190;2.中国科学院研究生院,北京 100049)

随着现代战争格局的改变和航天需求的增大，空间拦截显得日益重要.而末制导的精确与否决定拦截器最终能否拦截到目标.关于空间拦截的制导律问题很多人都已经研究过，如比例导引律[1-2]、非线性制导律[3-4]，这些控制方法有的比较复杂，使用起来不方便，需要发动机提供变推力，工程实现较难，而且不具有抗外界干扰能力.理想滑模控制虽然具有对外界干扰的不变性，但是存在抖振问题[5].

本文针对发动机工作特性，依据准滑模控制思想提出一种操作起来简单，又能控制精度的末制导律.该制导律易于工程实现，而且当边界层趋于零时，具有很好的抗干扰性.

1 空间拦截问题的数学描述

本体坐标系及视线坐标系的数学描述如图1所示.其中：本体坐标系为Oxbybzb，其坐标原点O定义在拦截器质心，在零姿态情况下，Oxb为拦截器滚动轴，指向卫星飞行方向，Oyb为拦截器俯仰轴，Ozb为拦截器偏航轴，指向地心；视线坐标系为Oxsyszs，其坐标原点O定义在拦截器质心，Oxs由拦截器质心指向目标航天器质心，Oys和Ozs由本体坐标系通过高低角θ和方位角φ来确定.

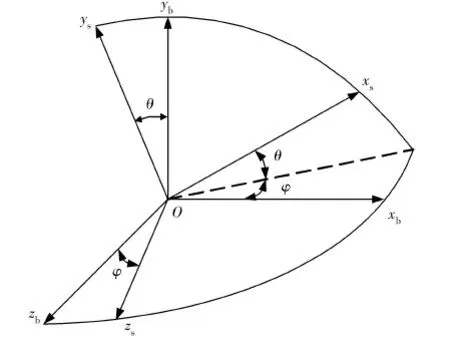
图1 视线坐标系和本体坐标系

两坐标系之间的转换关系如下：

(1)

(2)

式中，x1是拦截器和目标航天器的相对距离，x2是拦截器和目标航天器的相对速度，x3是纵向平面的视线角速度，x4为横向平面的视线角速度，u1是拦截器在zb轴上的推力加速度，u2是拦截器在yb轴上的推力加速度.

控制时，可以对纵向平面和横向平面分别进行控制.

对纵向平面的控制可以表示为

(3)

对横向平面的控制可以表示为

(4)

2 制导律设计

以纵向平面控制为例，采用准滑模控制方法进行制导律设计.

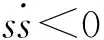
空间拦截最终要实现拦截器以一定的速度撞击目标，这就要求x1=0而x2≠0.选取切换函数

s=x3

(5)

这样就可以保证拦截器以一定的速度撞击目标.

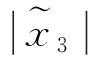
(6)

式中Tb为允许的最大脱靶量，B为盲区最大允许范围，tf为进入盲区的时刻.

选取制导律为

(7)

式中U为发动机提供的推力加速度.

如果Δ选取得太大，精度就达不到要求，会产生脱靶现象；如果Δ选取得太小，就会造成发动机的频繁开关机，不能有效地减少抖振.Δ的选取与x3所要达到的精度有关，即与脱靶量有关.

横向平面的控制与纵向平面的控制类似.

3 数学仿真

设仿真初值为：x1(0)=5×104m，x2(0)=-2.5×103m/s，x3(0)=6×10-4rad/s.发动机提供的加速度U=10m/s2.制导律中，边界层Δ取为1×10-5.采用准滑模控制，仿真结果如图2～5所示.

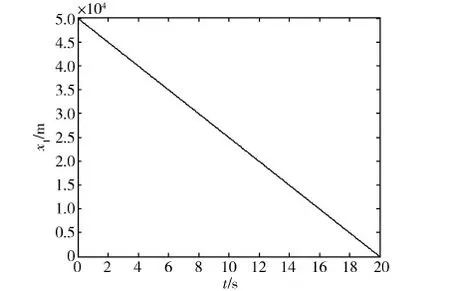
图2 采用准滑模控制时相对距离随时间的变化

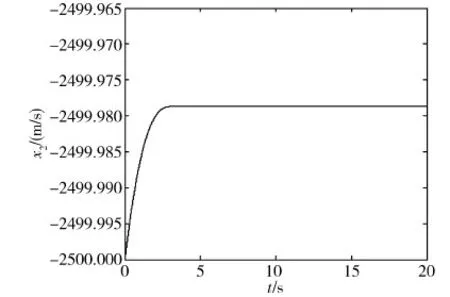
图3 采用准滑模控制时相对速度随时间的变化

图4 采用准滑模控制时视线角速度随时间的变化

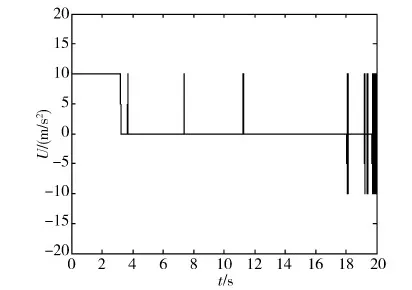
图5 采用准滑模控制时发动机开关状态

从图2～5的仿真结果可以看出，在准滑模制导律的作用下，视线角速度保持在预定的精度范围内，使得相对距离能够收敛到满足脱靶量要求的数值，从而保证拦截器以一定的相对速度撞击目标.而且这种制导律操作简单，控制过程中开关机频率不是很高，易于工程实现.

如果采用理想滑模控制，即Δ=0，仿真结果如图6～9所示.

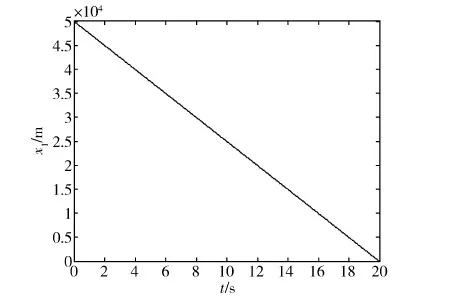
图6 采用理想滑模控制时相对距离随时间的变化

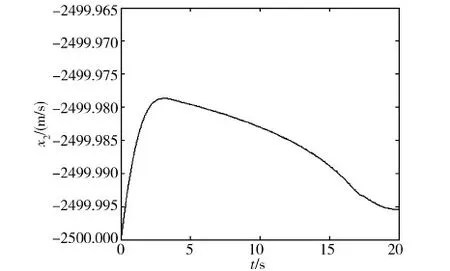
图7 采用理想滑模控制时相对速度随时间的变化

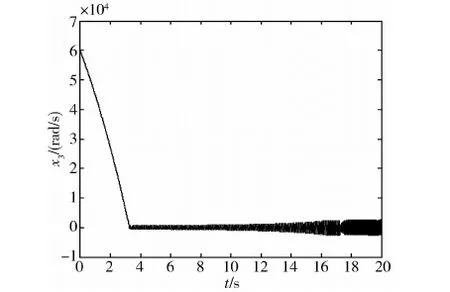
图8 采用理想滑模控制时视线角速度随时间的变化

图9 采用理想滑模控制时发动机开关状态

对比图5和图9可以看出，采用准滑模控制后，发动机的开关机频率明显降低，有效地抑制了抖振，而理想的滑模控制发动机的开关机则过于频繁，在实际应用中很难实现.

4 结 论

本文主要研究了准滑模制导律在空间拦截中的应用，并进行了数学仿真和对比.仿真结果表明：采用准滑模控制有效地降低了发动机的开关机频率，削弱了抖振，并能够控制精度，实现最终的空间拦截；而且该制导律相对简单，易于实现.