一类积图的测地数

王 兵，吕长虹，张 梅

（1.华东师范大学 数学系，上海200062；2.滁州学院 数学系，安徽 滁州239000）

一类积图的测地数

王 兵1，2，吕长虹1，张 梅2

（1.华东师范大学 数学系，上海200062；2.滁州学院 数学系，安徽 滁州239000）

图中的度量空间是（V（G），d），测地数是其中的一个重要参数.强积图是图与图之间通过一种乘积运算得到的图.文中得到了极点测地图的强积图的测地数，由此得到了树的强积图的测地数。

测地数；强积图

0 引言

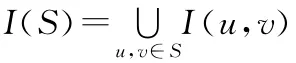
对于u∈V（G），若u的闭邻域是一个团，则称u为图G的一个极点.我们记Ext（G）为G中的极点集，显然Ext（G）必须包含在G的任一测地集中，从而｜Ext（G）｜≤g（G）.若图G满足｜Ext（G）｜＝g（G），则称G为极点测地图（extreme geodesic graph）.为了方便，将所有的极点测地图构成的集合记为Γ.这类图被G.Chartrand，P.Zhang等人在文献［2］中提到和研究.

下面介绍图的一种积运算：也称为图G，H的强积图［3］，记为G⊗H，它的顶点集为：

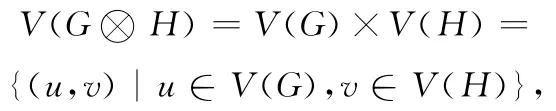
并满足两顶点（u1，v1），（u2，v2）（ui∈V（G），vj∈V（H）；i，j＝1，2）在G⊗H邻接当且仅当

（1）u1＝u2且v1，v2在H中邻接，或

（2）v1＝v2且u1，u2在G中邻接，或

（3）u1，u2在G中邻接且v1，v2在H中邻接.

在本文中，我们主要研究一类特殊的图即极点测地图（extreme geodesic graph）的结构，给出两个极点测地图的强积图的测地数，由此推出任意两个树的强积图的测地数.

1 预备知识

这一节，我们介绍一些测地数的相关结果和强积图的测地集的一些性质.

引理1［1］图G的极点属于G的任一个测地集.特别地，度为1的点属于G的任一个测地集.

引理2［3］设图G1，G2为连通图，且（u，v），（u′，v′）为G1⊗G2中的任意两顶点，则有：

2 主要结果

我们首先研究两极点测地图G1，G2的强积图G1⊗G2的测地数，然后给出它的一些应用.

定理3 设G1，G2∈Γ且｜G1｜，｜G2｜≥2.m1，m2分别为G1，G2的极点数，分别记：

为对应于G1，G2中的极点集.则有：

（1）（e1i，e2j）（i＝1，2，…，m1；j＝1，2，…，m2）为G1⊗G2的极点.

（2）g（G1⊗G2）＝m1×m2，且S＝｛（e1i，e2j）｜（i＝1，2，…，m1；j＝1，2，…，m2）｝为G1⊗G2的最小测地集.

证明 （1）考虑G1⊗G2中的顶点（e1i，e2j），因为e1i，e2j分别为G1，G2中的极点，不妨设e1i，e2j在G1，G2中的邻居分别为u1，…，up；v1，…，vq（p，q≥1）.则（e1i，e2j）在G1⊗G2中的邻居为三类点：（e1i，vt），（us，e2j），（us，vt）（s＝1，…，p；t＝1，…，q）.由强积图的定义，这三类点中任两个点都邻接.所以（e1i，e2j）为G1⊗G2中的极点.

（2）由（1）和引理1的结果，可知g（G1⊗G2）≥m1×m2＝｜S1×S2｜＝｜S｜，下面我们证明S为G1⊗G2的一个测地集.为此，只需证明G1⊗G2中的任意顶点x，都位于某条端点在S中的测地线上.分四种情形讨论：

（a）存在某个1≤i≤m1，1≤j≤m2使得：x＝（e1i，e2j），这时有x∈S，结论显然成立；

（b）存在某个1≤i≤m1使得：x＝（e1i，v），其中v∈V（G2）＼｛e21，e22，…，e2m2｝，这时v在G2中必位于某条以G2中两极点为端点的测地线上，不妨设位于e2s－e2t（1≤s≠t≤m2）测地线上.结合引理2有：

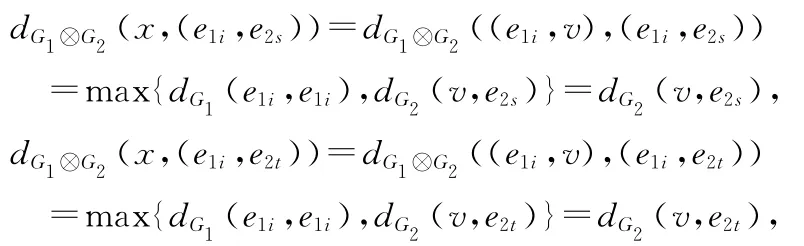
又由v位于e2s－e2t（1≤s≠t≤m2）测地线上，我们可以得到：

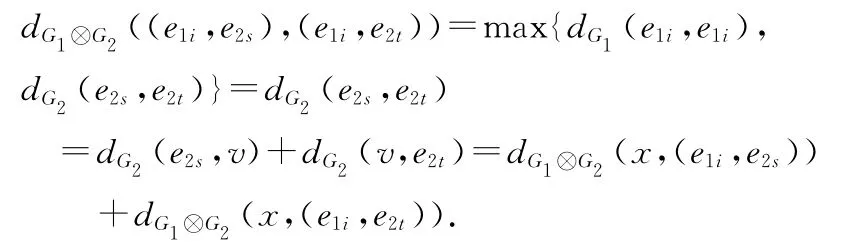
即x位于（e1i，e2s）－（e1i，e2t）测地线上.

（c）存在某个1≤j≤m2使得：x＝（u，e2j），其中u∈V（G1）＼｛e11，e12，…，e1m1｝.类似（b）可证.

（d）x＝ （u，v），u∈V（G1）＼｛e11，e12，…，e1m1｝，v∈V（G2）＼｛e21，e22，…，e2m2｝.我们考虑G1中所有过u点且端点均为极点的测地线族，记S′1为这个测地线族的所有端点的并，显然S′1⊆S1.类似地记G2中对应的集合S′2.令

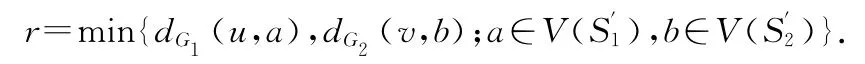
不失一般性，设对某个1≤i≤m1，有dG1（u，e1i）＝p.G2中存在e2s，e2t∈S′2，使得v位于e2s－e2t测地线上.下证x位于（e1i，e2s）－（e1i，e2t）测地线上.

结合引理2与r的最小性，得：

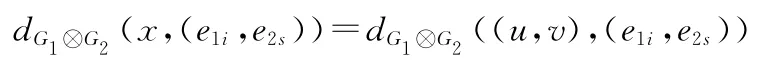
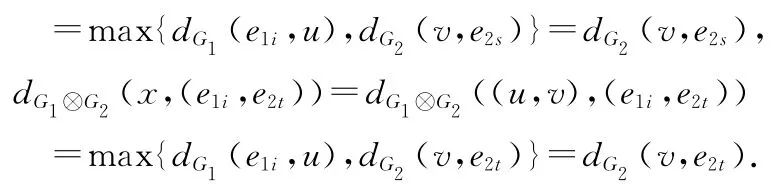
又由于v位于e2s－e2t测地线上，我们可以得到：

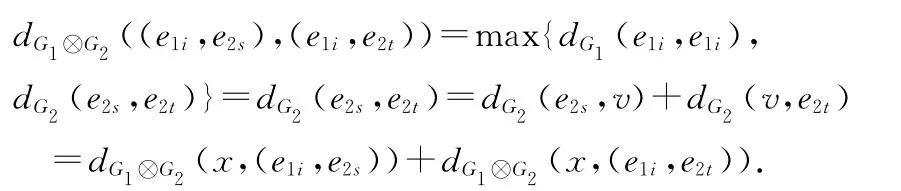
则x位于（e1i，e2s）－（e1i，e2t）测地线上.结合四种情形，结论得证.

定理4［4］设树T有m个叶子l1，l2，…，lm，则g（T）＝m且｛l1，l2，…，lm｝为它的最小测地集.

推论5 设T1，T2为阶数不小于2的树，m1，m2分别为T1，T2的叶子数，则g（T1⊗T2）＝m1m2.

证明 结合引理1和定理4可知T1，T2∈Γ，极点数分别为m1，m2，由定理3可得结论.

［1］G..Chartrand，P.Zhang，The geodetic number of an oriented graph［J］，European J Combin，2000（21）：181－189.

［2］G.Chartrand，P.Zhang，Extreme geodesic graphs［J］，Czechoslovak Mathematical Journal，2002（52）：771－780.

［3］W.Imrich，S.Klavzar.Product graphs：Structure and Recognition［M］，Wiley－Interscience，New York，2000.

［4］M.Farber，R.E.Jamison.Convexity in graphs and hypergraphs［J］，SIAM J.Algorithn Disc Math.1986（7）：433－444.

［5］吕长虹.图和有向图的测地数［J］.中国科学 A辑.2007（37）：579－586.

The Geodesic Number of Strong Product Graphs

Wang Bing1，2，Lu Changhong1，Zhang Mei2
（1.Department of Mathematics，East China Normal University，Shanghai 200062，China；2.Department of Mathematics，Chuzhou University，Chuzhou 239000，China）

It is known that（V（G），d）is a metric space on a graph G，where geodesic number is an important parameter.A strong product graph is obtained from two graphs by aproduct operation.This paper obtains the geodesic numbers of strong product of two extreme geodesic graphs.As a corollary，the geodesic number of strong product of two trees is given.

geodesic number；strong product graphs

O157

：A

：1673－1794（2010）05－0016－02

王 兵（1982－），男，华东师范大学在职研究生，研究方向：图论。

安徽省教育厅自然科学研究项目（kj2009B002）

2010－11－12