Banach空间中一阶非线性微分方程组的终值问题解的存在性
2010-11-02张海燕
张海燕
(宿州学院 数学与统计学院,安徽 宿州234000)
Banach空间中一阶非线性微分方程组的终值问题解的存在性
张海燕
(宿州学院 数学与统计学院,安徽 宿州234000)
用Mnch不动点定理,研究了Banach空间中一阶微分方程组的终值问题,在较宽松的条件下获得了解的新存在性定理,改进和推广了某些已知的结果.
Banach空间;终值问题;Mnch不动点定理;非紧性测度
1 引言
有关一阶非线性常微分方程终值问题,文献[1-2]在实空间对终值问题作了基础性讨论,文献[3-4]利用锥理论结合上下解方法将其推广到Banach空间中,得到了更为一般的结果,文献[5]在一定的紧型条件下,对系数加以限制,利用Sadovskii不动点定理给出了其解的存在性定理,他们所用的限制性条件都较为严格,对先验估计和非紧性测度估计有较强的要求.而且对于Banach空间方程组的终值问题至今未有很好的结果,受文献[1-6]启发,本文去掉了上述一些较强的限制性条件,在较宽松的条件下,利用Mnch不动点定理,获得了Banach空间一阶微分方程组的终值问题解的存在性定理.
令(E,‖·‖)是 Banach空间,J=[0,+∞),R+=(0,+∞),f,g∈C[J×E×E,E],u∞∈E且有界.本文考察Banach空间E中一阶非线性微分方程组的终值问题(TVP):
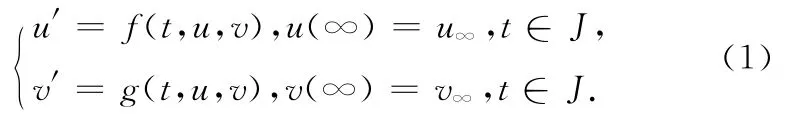
2 预备知识和引理

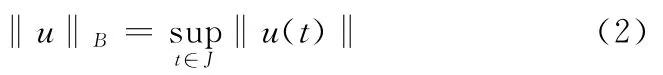
易知(BC[J,E],‖·‖B)为Banach空间.令X=BC[J,E]×BC[J,E],定义范数
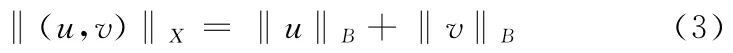
可证X在范数‖(u,v)‖X下为一Banach空间.定义算子A:X→X如下:

其中
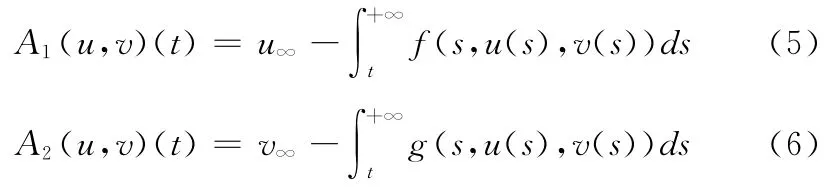
对Banach空间中的有界集C,用α(C)表示Kuratowski非紧性测度.有关非紧性测度的详细定义及性质参见文献[7].另记Br={u∈BC[J,E]|‖u‖≤r}(r>0).
下面给出几个我们需要用到的引理:
引理1[8]设m(t),γ(t)∈C[J,R+],,若,t∈J,其中K≥0,M>0,则,t∈J.
引理2[5]设B={un(t)}⊂C[J,E],若存在ρ(t)∈L[J,R+],使得‖un(t)‖<ρ(t)(n=1,2,…),则α(B(t)),在R+上可积,并且

引理3[9](Mnch定理)设E是Banach空间,Ω⊂E是有界开集,θ∈Ω,A:E→E是一个连续算子,且满足下列条件:
(1)x≠λAx,∀λ∈[0,1],x∈∂Ω;
3 主要定理
为方便叙述,先列出下列假设:
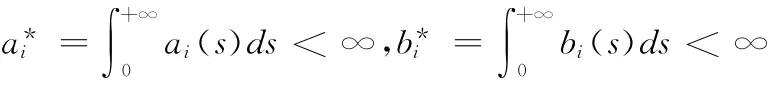
‖f(t,u,v)‖≤a1(t)+a2(t)‖u‖+a3(t)‖v‖,
‖g(t,u,v)‖≤b1(t)+b2(t)‖u‖+b3(t)‖v‖;
(H2)∀t∈J和H1,H2⊂Br,存在ci(t),di(t)∈C[J,R+],,使得
α(f(t,H1,H2))≤c1(t)α(H1)+c2(t)α(H2),
α(g(t,H1,H2))≤d1(t)α(H1)+d2(t)α(H2).
定理3.1 假设条件(H1)-(H2)成立,则TVP(1)在BC[J,E]∪C1[J,E]×BC[J,E]∪C1[J,E]中至少有一个解.
证明 由算子 A的定义易知(u,v)∈BC[J,E]∪C1[J,E]×BC[J,E]∪C1[J,E]是TVP(1)的解等价于(u,v)∈X是算子A的不动点.类似于文[6]的证明方法,容易证明A是连续算子.下面证明算子A至少有一个不动点.
首先证明Ω0={(u,v)∈X|(u,v)=λA(u,v),0≤λ≤1}是X中的有界集.
事实上,任给(u,v)∈Ω0,则存在0≤λ≤1,使得
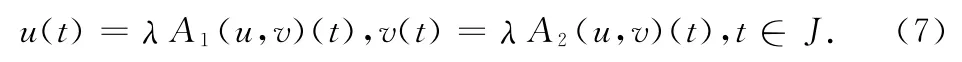
当t∈J=[0,+∞)时,由(5)-(7)式及假设(H1)得

令
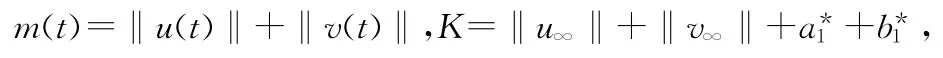
则m(t)∈C[J,R+],于是结合(8)(9)式得
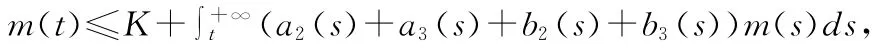
故由引理1知:
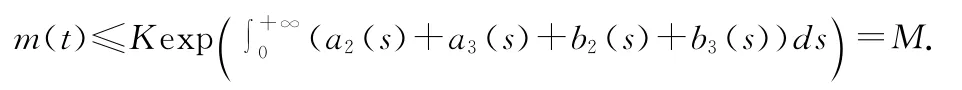
因此,‖u‖B+‖v‖B≤M,t∈J,即‖(u,v)‖X≤M,故Ω0是X中的有界集.
取R>M,令Ω={(u,v)∈BC[J,E]|‖(u,v)‖X<R},则Ω为X中的有界开集.并且(θ,θ)∈Ω,对任何(u,v)∈∂Ω,(u,v)≠λA(u,v),∀λ∈[0,1].即引理3的条件(1)满足.
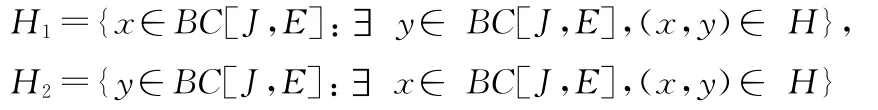
则

由(5)(6)式和假设(H1)容易证明Ai(H1×H2)(i=1,2)
在区间J上是等度连续的,从而由(10)式推出Hi(i=1,2)
在区间J上是等度连续的.令
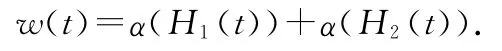
由非紧性测度的性质,算子A的定义,假设(H1),(H2)和(10)及引理2,我们有
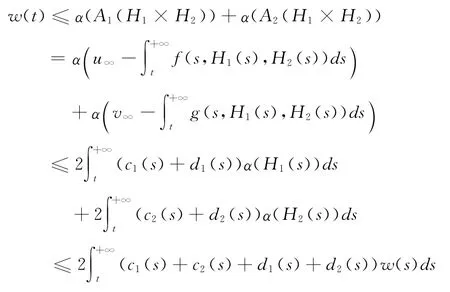
于是由引理1知,w(t)=0,t∈J,于是α(Hi(t))=0(i=1,2),t∈J.即Hi(i=1,2)是BC[J,E]中的相对紧集,由(10)可知,H是X中的相对紧集,引理3的条件(2)满足.故由引理3知,A在Ω内至少有一个不动点.
从而TVP(1)在BC[J,E]∩C1[J,E]×BC[J,E]∩C1[J,E]中至少有一个解.证毕.
注1 当E=R1时,本文定理1的结论仍然成立,因此本文推广了[1-2]中的结果.
注2 文[5]在使用Sadovskii不动点定理研究TVP(1)时,使用了先验估计的限制性条件:
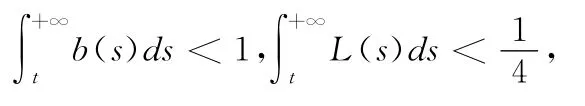
本文去掉了上述的限制性条件,利用不动点定理获得了方程组的终值问题解的存在性定理,对于单个方程情形也是成立的.
注3 文[6]在研究无穷区间方程组解的存在性时,要求f(t,H1,H2),g(t,H1,H2)在Br上是相对紧的,这是非常强的要求.本文条件相对弱得多.
注4 本文方法不同于文[1-6],且去掉了文献中的先验估计和紧性条件,在较宽松的条件下得到了无穷区间解的存在性定理.
4 应用
考虑一阶非线性微分方程组的终值问题:

结论 终值问题(11)至少有一个解.
证 令
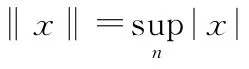
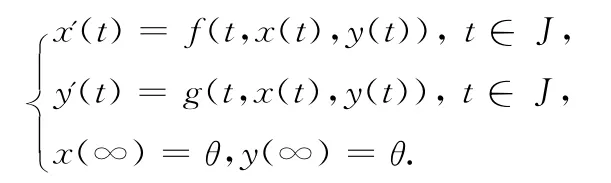
其中

而
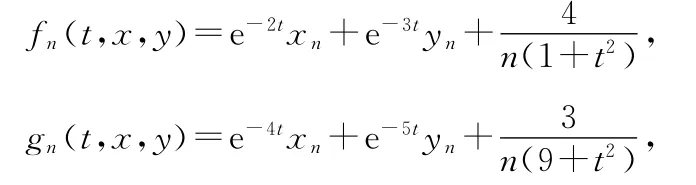
显然f,g∈C[J×E×E,E].
对∀x,y∈E,
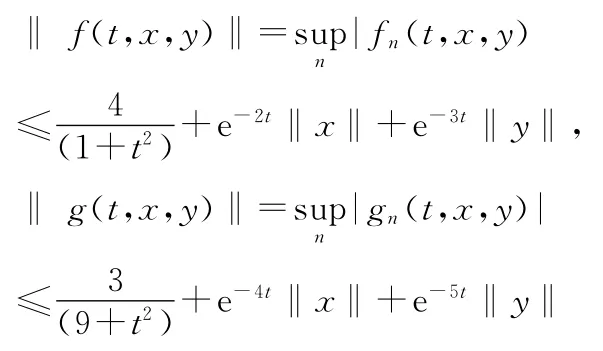
即
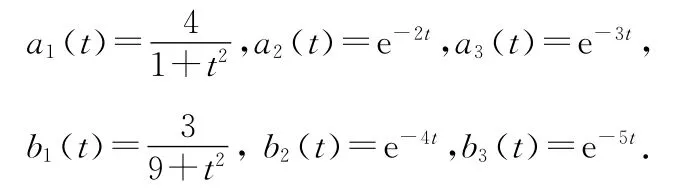
类似文[10]中例题的方法容易知,存在c1(t)=e-2t,c2(t)=e-3t,d1(t)=e-4t,d2(t)=e-5t.且,,使得对任何t∈J,有界集H1,H2⊂E,
α(f(t,H1,H2)<c1(t)α(H1)+c2(t)α(H2),α(g(t,H1,H2)<d1(t)α(H1)+d2(t)α(H2),故条件(H2)满足.由定理1即知结论成立.
[1]Aftabizadeh A.R,Lakshmikantham V.On the theory of terminal value problems for ordinary differential equations[J].Nonlinear Analysis,1981(5):1173-1180.
[2]郭大钧,孙经先,刘兆理.非线性常微分方程泛函方法[M].济南:山东科技出版社,1995:12-15.
[3]Qi Shishuo.Extremal solutions of terminal value problems for nonlinear impulsive intergo-differential equations in Banach spaces[J].Appl.Math.J.Chinese Univ,2000,15(1):37-44.
[4]Zhou Youming.The solution of extremal value problems for first order differential equation[J].Systems sci.Math.Sci.1999,19(3):264-267.
[5]李 莹,秦丽娟.无穷区间上Banach空间终值问题解的存在性[J].甘肃科学,2005,17(1):13-15.
[6]Liu Zhenbin,Liu Lishan.The existence of positive solutions of infinite boundary value problems in a Banach space for first order differential systems[J].Acta Math.Sinica,2007,50(1):97-104.
[7]郭大钧.非线性泛函分析[M].济南:山东科技出版社,2001.
[8]张海燕,李耀红.Banach空间中一阶非线性微分方程终值问题解的存在性[J].淮北煤炭师范学院学报,2008,29(4):12-15.
[9]Deimling Klaus.Nonlinear Functional Analysis[M].Berlin:spring-Verlag,1985.
[10]Zhang Xingqiu.Infinte boundary value problems for first order differential in a Banach[J].Math.Appl,2005,18(1):153-160.
Existence of Solutions of Terminal Value Problems for Nonlinear First Order Differential Equations Systems in Banach Spaces
Zhang Haiyan
(School of Mathematics and Statistics,Suzhou University,Suzhou 234000,China)
By using Mnch fixed theorem,we study existence of solutions of terminal value problems for nonlinear first order differential equations systems in Banach spaces.Under weaker conditions,the new existence theorem is obtained and some known results have been improved.
Banach spaces;terminal value problems;Mnch fixed point theorem;measure of noncompactness
0177.91
:A
:1673-1794(2010)05-0004-03
张海燕(1980-),女,讲师,硕士,研究方向:应用非线性泛函分析。
高校省级自然科学项目(KJ2010B226),宿州学院自然科学基金(2009yzk17)
2010-07-22
