沪深股市波动相关性的实证研究
2010-11-02武以敏刘小茂
武以敏,刘小茂
(宿州学院 数学系,安徽 宿州234000;华中科技大学 数学与统计学院,湖北 武汉430074)
沪深股市波动相关性的实证研究
武以敏,刘小茂
(宿州学院 数学系,安徽 宿州234000;华中科技大学 数学与统计学院,湖北 武汉430074)
文章选取上证指数和深成指数的收益率数据,使用时间序列分析的方法,利用向量自回归模型(VAR)及脉冲响应函数探讨了两个股市之间波动相关性的问题,得到两个市场存在明显的联动关系,通过上证综指滞后五期的收益可以预期深圳成指当期的收益,同样,通过深圳成指滞后六期的收益可以预期上证综指的当期收益.
股票指数;收益率;VAR模型;脉冲响应函数
1 引言
早在20世纪60年代,Fmaa(1965)[1]就观察到投机性价格的变化和收益率的变化具有稳定时期和易变时期,即价格波动呈现集群性,方差随时间变化.自回归条件异方差模型(ARCH 模型)最早由 Engel[2]提出,并由 Bollerslev[3]发展称为GARCH模型——广义自回归条件异方差模型.这些模型广泛应用于经济学的各个领域,尤其是用在金融时间序列分析中.1980年C.A.Sims将VAR模型引入到经济学中,推动了经济系统动态性分析的广泛应用.VAR模型常用于预测相互联系的时间序列系统及分析随机扰动对变量系统的动态冲击,从而解释各种经济冲击对经济变量形成的影响.Engle和Granger将协整与误差修正模型结合起来,建立了向量误差修正模型(VEC).VEC模型是含有协整约束的VAR模型,多应用于具有协整关系的非平稳时间序列建模[4].
本文主要使用ARCH类模型对沪深市场收益率的波动性进行分析,利用向量自回归模型(VAR)及脉冲响应函数探讨了两个股市之间波动相关性的问题.
2 数据分析
我们采用的数据均为深圳成指和上证综指每日的收盘价指数,即日内数据,选取自2005年1月4日至2009年3月11日共1013个日内数据进行分析.
每日的收盘价用xt表示,用rt表示每日的收益率,其中:
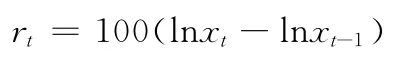
使用eviews5.0对收益率数据进行统计分析[5],结果如下.

表1 统计结果分析
从表1中可以看出,深圳成指的收益率均值为0.095267,标准差为2.266019,上证综指的收益率的均值为0.053604,标准差为2.088562,均值都远小于标准差,说明市场波动很大;两个偏度都满足S<0,分布都向右偏有个较长的左尾部.深圳股市峰度K=4.854607>3,上海股市峰度K=5.434092,说明它们的收益率分布都呈尖峰分布.J-B检验的概率几乎为零,说明收益率序列都不服从正态分布.股指收益率在零均值附近上下波动,波幅小于±10%,其波动表现出金融时序数据典型的集聚性、爆发性、持久性等特征.
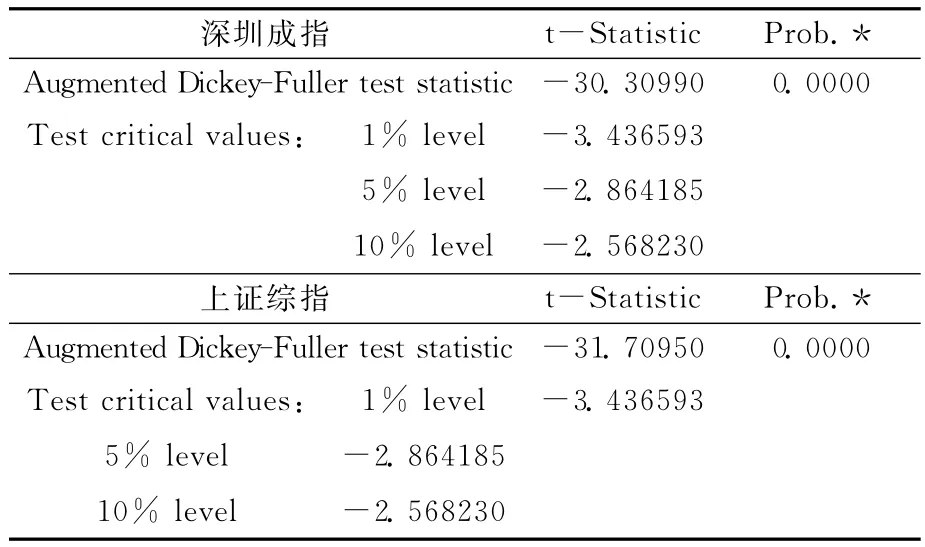
表2 ADF检验结果
先我们对序列的平稳性进行判断.检验序列平稳性的方法是单位根检验,这里我们使用的是ADF检验.
ADF检验结果表示两个序列都是平稳的时间序列.
为了检验股票价格指数的波动是否具有条件异方差性,先检验其残差序列是否还有ARCH效应.这里我们采用的是拉格朗日乘数检验即ARCH-LM检验.
利用ARCH-LM检验,对残差序列进行ARCH检验,结果如表3:

表3 ARCH-LM检验结果
检验的相伴概率P几乎为零,拒绝残差序列不存在ARCH效应的原假设,说明股票收益率序列存在着ARCH效应.
3 VAR模型及脉冲响应函数分析
3.1 VAR模型的选取
VAR(p)模型的数学表达式是[4]:

其中:yt是k维内生变量,xt是d维外生变量向量,p是滞后阶数,T是样本个数.多元时间序列rt是一个一阶的VAR过程,或者简称为VAR(1),如果它服从下面的模型:

这里φ0是一个k维向量,Φ是一个k×k维矩阵,{at}是序列不相关的随机向量序列,其均值为0,协方差矩阵为∑.实际应用中,要求协方差矩阵是正定的;否则可以简化rt的维数.通常假定at是多元正态的.
VAR模型中一个重要的问题就是滞后阶数的确定.在选择滞后阶数p时,一方面想使滞后数足够大,以便能完整反映所构造模型的动态特征.但是另一方面,滞后数越大,需要估计的参数也就越多,模型的自由度就减少.所以通常进行选择时,需要综合考虑,既要有足够数目的滞后项,又要有足够数目的自由度.
使用Eviews软件[9],根据滞后长度准则选取建立滞后期为多少的VAR模型最为合理,我们将结果列入表4,5个评价统计量各自给出的最小滞后期用“*”号表示.结果表明,建立六阶的VAR模型比较合理.
3.2 模型结果分析
通过约翰森检验,证实深圳股市、上海股市两市场的波动性之间存在着一阶协整关系,结果如表5:

表4 VAR模型滞后阶数的选取

表5 约翰森检验结果
结果显示两个市场的收益率存在长期协整关系,因此,通过建立向量误差修正模型(VEC),验证两个市场间的相互葛兰杰(Granger)因果关系.一个变量如果受到其他变量的滞后影响,则称它们具有Granger因果关系.
在此,我们选取六阶滞后VEC模型.结果如表6所示:

表6 向量误差修正模型结果
根据结果给出VEC模型的回归方程为:


上式中,DSZ、DSH分别表示深圳股市、上海股市异常收益率方差的一阶差分,DSZ(-i)、DSH(-i)分别表示异常收益率方差一阶差分的滞后i期.
根据回归系数的t值的数值,可以得到:上证综指的收益率能够影响深成指数的收益率,通过上证综指滞后五期的收益可以预期深圳成指当期的收益,说明上证综指是深证成指的葛兰杰原因.同样,深圳成指的收益率能够解释上证综指的收益率变化,说明深圳成指也是上证综指的葛兰杰原因,通过深圳成指滞后六期的收益可以预期上证综指的当期收益.两个市场间存在着明显的联动关系.
在上面的VEC模型上得出30期的脉冲响应函数图如图1.图中SER01表示深圳成指,SER02表示上证综指.横轴表示冲击作用的滞后期数(单位:日).

图1 脉冲响应函数图
可以看到,上证综指收益率的一个单位标准差新息对深圳成指收益率的影响不是很大,但响应程度第1期为0,第6期达到最大值0.081响应程度为正,其余各期响应程度均为负向,并且影响是长期的,响应程度渐趋于-0.119.深圳成指收益率对自身的一个标准差新息立即有较强的反映,其响应程度达到2.378,但自第2期开始响应程度渐趋于0.614,影响是长期的.深圳成指受益率的一个单位标准差新息对上证综指收益率的影响很大,其响应程度在第1期达到2.028以上,但是影响时间不长,第2期便回复到0.268,之后渐渐趋于0.474.上证综指收益率对自身的一个标准差新息反映不是很大,响应程度第1期为0.781,第2期时响应程度为负向,第6期为0.032,之后渐趋于-0.0939.
我们用深圳成指(RSZ)作为被解释变量,上证综指和深圳成指滞后六阶作为解释变量,进行脉冲响应函数回归.可以得到预测方程如下:

可以得到,T期深圳成指收益率一个单位的变动,引起T+1期深圳成指0.234452个单位的变动,T+2期0.087169个单位的变动,T+3期0.016075个单位的变动,T+4期0.028597个单位的变动,T+5期-0.222567个单位的变动,T+6期0.191061个单位的变动;T期上证综指收益率一个单位的变动,引起T+1期深圳成指-0.215221个单位的变动,T+2期-0.148061个单位的变动,T+3期0.029743个单位的变动,T+4期0.077094个单位的变动,T+5期0.243983个单位的变动,T+6期-0.264960个单位的变动.
用上证综指(RSH)作为被解释变量,上证综指和深圳成指滞后六阶作为解释变量,进行脉冲响应函数回归.可以得到预测方程如下:

可以得到,T期上证综指收益率一个单位的变动,引起T+1期上证综指0.075517个单位的变动,T+2期0.044835个单位的变动,T+3期0.058440个单位的变动,T+4期0.045658个单位的变动,T+5期-0.157646个单位的变动,T+6期0.188392个单位的变动;T期深圳成指收益率一个单位的变动,引起T+1期上证综指-0.072081个单位的变动,T+2期-0.067793个单位的变动,T+3期-0.009735个单位的变动,T+4期0.037234个单位的变动,T+5期0.164814个单位的变动,T+6期-0.250468个单位的变动.
4 结论
本文主要研究中国金融市场的波动变化,以上证综指和深圳成指的股指波动情况代表中国金融市场的走势,通过VAR模型,分析了上海股市与深圳股市之间的波动关系.实证研究得出以下结论:
第一,上海股市和深圳股市收益率分布都具有尖峰厚尾的特征,波动率表现出金融时间时序数据典型的积聚性、爆发性、持久性等特征,并且都存在高阶的ARCH效应.
第二,两个股票市场之间存在着明显的联动关系.通过上证综指滞后五期的收益可以预期深圳成指当期的收益,同样,通过深圳成指滞后六期的收益可以预期上证综指的当期收益.
[1]Eama,E.The Behavior of Stock Market Prices[J].Journal of Business,1965.38.
[2]Engle RF.Autoregressive conditional heteroskedasticity with estimates of the variance of United Kingdom inflation[J].Econometrica,1982,50:987-1007.
[3]Bollerslev T.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics,1986(31):307-327.
[4]Ruey S.Tsay著,潘家柱译.金融时间序列分析[M].机械工业出版社,2006.
[5]高铁梅.计量经济分析方法与建模:Eviews应用及实例[M].清华大学出版社,2006.
[6]潘红宇.时间序列分析[M].对外经济贸易大学出版社,2006.
[7]于俊年.计量经济学软件——Eviews的使用[M].对外经济贸易大学出版社,2006.
[8]周 建.时间序列建模中滞后阶数选取准则函数的检测效力及其特征[M].系统工程理论与实践,2005(11):20-27.
[9]张晓峒.Eviews使用指南与案例[M].机械工业出版社,2008.
An Empirical Study of Fluctuating Correlation between Shanghai and Shenzhen Stock Market
Wu Yimin1, Liu Xiaomao2
(1.Department of Mathematics,Suzhou College,Suzhou 234000,China;2.School of Mathematics and Statistics,Huazhong University of Science and Technology,Wuhan 430074,China)
The fluctuating correlation between Shanghai and Shenzhen stock market is discussed in this article by making analysis of the earning rate data of Shanghai Composite Index and Shenzhen Component Index using time series analysis,the vector auto-regressive(VAR)model and impulse response function.The result shows that there is a significant correlation between the two markets.The current income of Shenzhen Stock Exchange Component Index can be anticipated by the last five-period income of Shanghai Stock Exchange Composite Index,and likewise,the current income of Shanghai Stock Exchange Composite Index can be anticipated by the last six-period income of Shenzhen Stock Exchange Component Index.
stock index;rate of return;VAR model;impulse response function
O212;F8
:A
:1673-1794(2010)04-009-04
武以敏(1982-),女,硕士,讲师,研究方向:数理金融。
宿州学院自然科学研究项目(2009yzk16);宿州学院硕士启动基金项目(2008yss20)
2010-04-20
