一类二阶变系数线性微分方程的新解法
2010-11-02丁楠
丁 楠
(滁州学院 数学系,安徽 滁州239000)
一类二阶变系数线性微分方程的新解法
丁 楠
(滁州学院 数学系,安徽 滁州239000)
本文研究了二阶变系数线性微分方程的解法.通过寻找特解和变量代换的办法得到了一种新的求解一类二阶变系数线性微分方程通解的方法.
二阶变系数线性微分方程,特解,通解
0 引言
二阶线性微分方程具有很强的应用背景,在文献[1]中,作者对二阶常系数线性微分方程的通解求法作了详细介绍,但对二阶变系数线性微分方程通解,没有提供太多的求法.讨论二阶变系数线性微分方程的解法,有助于提高学生学习常微分方程的能力和解题能力.本文通过寻找特解和变量代换的方法得到了二阶变系数线性微分方程通解的求法.
1 主要结果
设n阶变系数线性非齐次微分方程
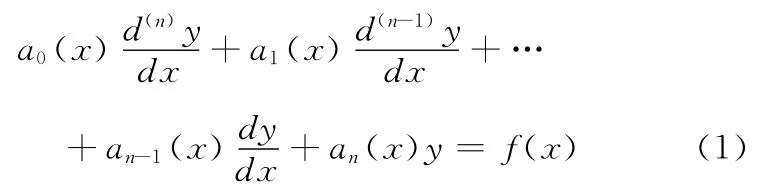
对应的齐次方程为

定理1 若方程(2)的特解为Y*(x),则方程(1)的通解为Y(x)=u(x)Y*(x).
定理2 对于n阶变系数线性齐次方程

有以下结论:
(1)若an-1(x)+xan(x)=0,则特解为y=x;
(2)若a0(x)+a1(x)+… +an(x)=0,则特解为y=ex;
(3)若(-1)na0(x)+(-1)n-1a1(x)+…+an(x)=0,则特解为y=e-x;
(4)若rna0(x)+rn-1a1(x)+…+an(x)=0,则特解为y=erx.
上述寻找特解的方法要求系数要满足一定的条件,有时并不好实现.而对于一些二阶变系数线性微分方程可通过变量代换化为常系数方程,从而很容易求解.
考虑二阶变系数齐次线性微分方程
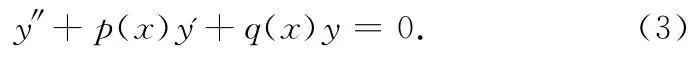
令t=u(x),则
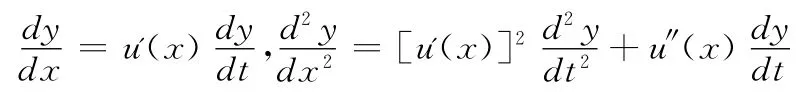
代入方程(3)得

若系数p(x),q(x)满足:
(a)u″(x)+p(x)u'(x)=0;
(b)[u'(x)]2+λq(x)=0,其中λ为常数,
则整理(a),(b)得,e-2∫p(x)dx+λq(x)=0.这样,我们就证明了以下结果.
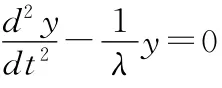
2 应用举例
例1 求方程xy″+2(1-x)y'+(x-2)y=2ex的通解.
解因为x+2(1-x)+(x-2)=0,则方程有特解y1=ex.于是,方程有形如y=u(x)ex的通解.将y=u(x)ex代入方程得
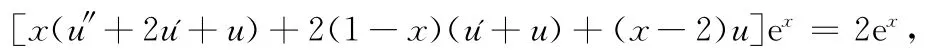
即

解方程(4)得

例2 求方程
xy″+(2x+1)y'+(x+1)y=(x2+x-1)e-x的通解.
解 因为x-(2x+1)+(x+1)=0,则方程有特解y1=e-x.于是,方程有形如y=u(x)e-x的通解.将y=u(x)e-x代入方程得

即

解方程(5)得

于是,原方程的通解为
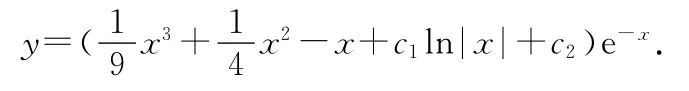
例3 解方程y″-y'cotx+4ysin2x=0
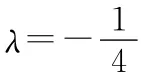

代入方程得

即

方程(6)为二阶常系数线性齐次微分方程,其通解为y=c1cos2t+c2sin2t.故原方程的通解为

例4 解方程xy″-y'-4x3y=x3ex2
解p(x)=-1/x,q(x)=-4x2.显然,存在常数λ=1/x,使得e-2∫p(x)dx+λq(x)=0.令t=x2,则
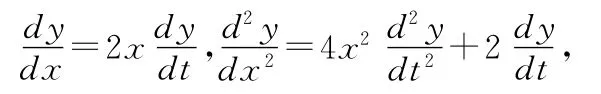
代入方程得

即


3 结论
本文讨论的仍然是一些具有特殊形式的二阶变系数线性微分方程,对于一般形式的二阶变系数线性微分方程的求解还有待于进一步研究.
[1]王高雄.常微分方程[M].北京:高等教育出版社,2006:120-156.
[2]陈惠汝,刘红超.二阶变系数线性微分方程的变量代换解法[J].高等函授学报(自然科学版),2008,21,(3):21-22.
[3]张金战.二阶变系数线性微分方程的特解[J].甘肃高师学报,2007,12(2):14-15.
[4]周 玲,张玲玲.关于二阶变系数线性微分方程的求解方法[J].安徽教育学院学报,2007,25(3):11-13.
[5]孟红丽,李文清.一类二阶变系数齐次线性微分方程的通解[J].西南民族大学学报(自然科学版),2009,35(4):726-729.
[6]范小勤,李金洋.变系数二阶线性微分方程的求解[J].高等函授学报(自然科学版),2009,22(3):41-42.
A New Solution to a Class of Second Order Linear Differential Equations with Variable Coefficients
Ding Nan
(Department of Mathematics,Chuzhou University,Chuzhou 239000,China)
In this paper,we present a new method of solving a class of second order linear differential equations with variable coefficients by means of searching special solution and variable substitution.
second order linear differential equations with variable coefficients;special solution;general solution
O175.1
:A
:1673-1794(2010)05-007-02
丁 楠(1981-),女,硕士,讲师,研究方向:微分方程稳定性理论。
安徽省应用数学省级教学团队建设项目,滁州学院院级教学项目(2009jyy025)
2010-06-15
