不允许卖空条件下不相关资产的实证分析

靳海娟，张作泉

（1.长治学院 数学系，山西 长治046000；2.北京交通大学 数学系，北京100044）

不允许卖空条件下不相关资产的实证分析

靳海娟1，张作泉2

（1.长治学院 数学系，山西 长治046000；2.北京交通大学 数学系，北京100044）

本文以选取的股票样本为依据，把传统的Markowitz模型和不允许卖空条件下不相关资产模型进行比较，通过相关数据的计算，证明了在相同收益的条件下，不相关资产模型能产生更小的风险，体现了不相关模型的优越性。因此，在实践中可以有效的指导投资者的投资行为。

投资组合；不允许卖空；允许卖空；不相关资产；实证分析

1952年，Markowitz发表了一篇题为“投资组合选择”的论文[1]，这个奠基性的工作对于金融学的发展所产生的影响是十分巨大和深远的。但是，Markowitz的理论并没有考虑投资比例系数的符号问题,由于负的投资比例系数意味着卖空相应的证券,而卖空程序在某些场合是很难实现的,所以研究不允许卖空条件下的资产组合理论有其实际意义。

本文引用了改进的不允许卖空条件下不相关资产的投资模型，并以深圳股市上选取的样本为依据验证了不存在无风险资产的情况下，改进的不允许卖空条件下不相关资产投资模型的可行性,并把其与传统的Markowitz不相关资产模型进行了对比研究，获得了更精确、更贴近实际、更有效的结果,从而能够指导投资者的投资行为。

本文研究的是无摩擦的情况，然而，在考虑了部分摩擦因素(如带交易费,税收等等)后，不允许卖空时证券组合有效前沿的分析表达式也应该可以相应的得到。这个问题有待读者考证。

一、Markowitz模型及不相关条件下的表示

当市场无摩擦且允许卖空时，标准的Markowitz均值方差模型：

Merton[2]给出了模型（M）的有效投资组合及有效前沿的解析表达式：

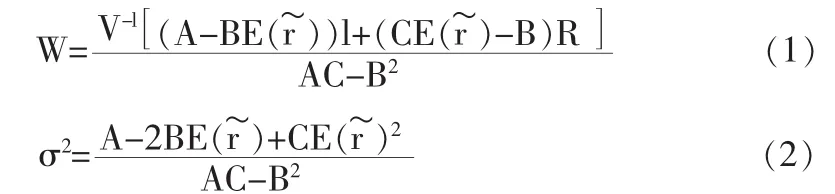
故式（1）可表示为：

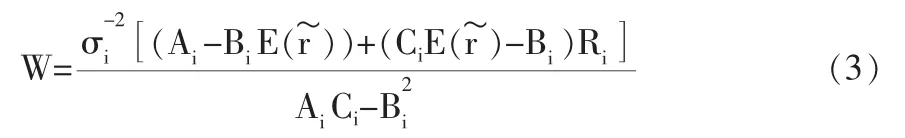
二、改进的不允许卖空条件下不相关资产的投资模型

当不考虑交易费且不允许卖空时,最优投资组合选择模型（M）就可等价地写成（M1）。

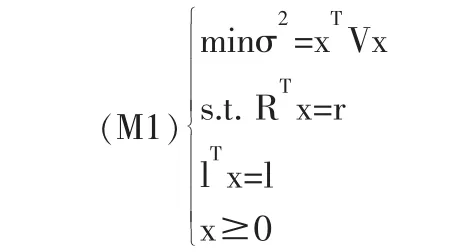
其中R=（R1，R2，…，Rn）为n种资产的期望收益率向量，r为给定的期望投资组合收益率，V=（σij）n×n是n种资产收益率的协方差距阵（假定为正定），l=（l，l，…，l）T是n维单位向量，x=（x1，x2，…，xn）T为投资组合（投资比例向量）。

模型 （M1）引起了众多学者的广泛重视。例如，Ross，Dybvig，Szego，杨德权等研究了有效投资组合的性质以及有效前沿的特征和解析表达式的确定方法,Markowitz提出了有效前沿的临界线算法,唐小我等提出了参数单纯形法。

此时最优投资组合选择模型成为：

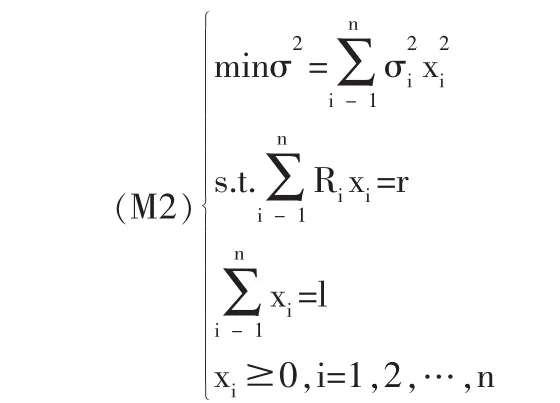
以下不妨假定记R1＜R2＜…＜Rn，记

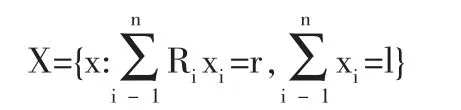
定理1[3]：当di-l燮r燮di（i=1，2，…，n-1）时，模型（M2）的最优投资组合为

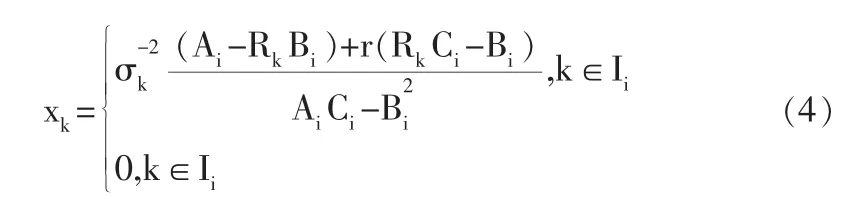
定理2[3]：模型（M2）的有效前沿是

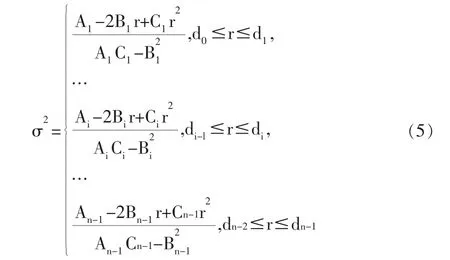
三、样本股的确定及计算结果

对于不允许卖空条件下不相关资产的投资组合，我们用实例来验证一下不存在无风险资产情况下的情形。

（一）样本股的确定

我们从深圳证券市场上的500多只股票中,按照行业代表性、流通市值规模、交易活跃程度、上市公司财务状况和经营业绩以及地区代表性等原则,优先从股本规模大、成长性较好的个股中选取了从2002年1月11日至2004年4月2日,约2年的周收盘数据作为本文的研究样本[4]。

为了研究方便我们做以下计算：

1.股票周收益率的计算：

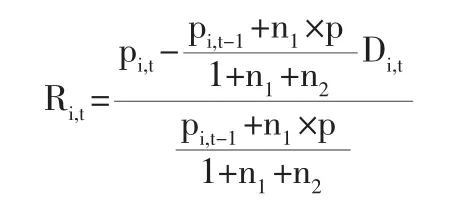
上式中，Ri,t为第i只股票第 t周的收益率；pi,t，pi,t-1分别为第i只股票在t，t-1周的价格；Di,t为第i只股票在第t周收取的现金股息；p为配股价；n1为配股比例；n2为送股比例。

2.第i只股票在这段时间中的平均周收益率为：

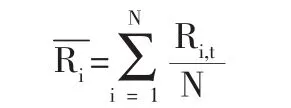
3.证券组合的平均周收益率和标准差公式为：

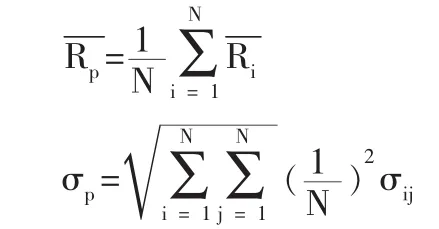
经过计算，得到各股的平均周收益率和标准差以及方差。根据平均周收益率大小，对这6只样本股进行从小到大的排序，见表1。

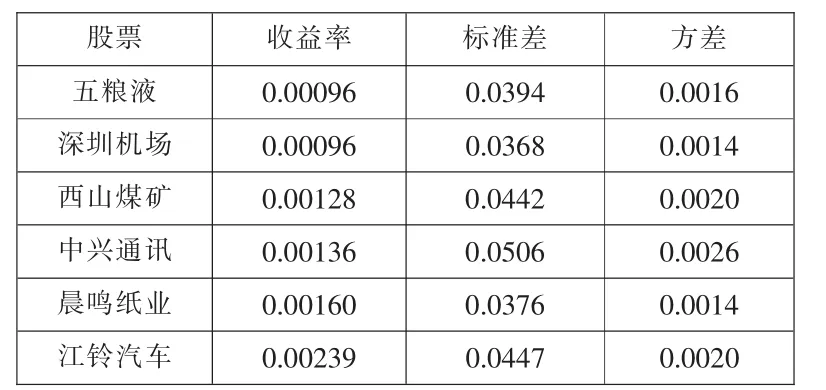
表1 ：样本股的平均收益率和标准差

（二）计算结果

由于我们选取的样本相互之间是不相关的,因此它们的协方差矩阵为对角矩阵,由表1我们可以得出所选取样本的协方差矩阵：

它的逆矩阵为：

且有

表2 ：各数值的计算结果

1.新模型的结果

用上面已经求得的数据我们来验证第4章中新建的不允许卖空条件下不相关资产模型。先把数据代入（4）式，并利用风险的计算公式，我们得到了以下数据：

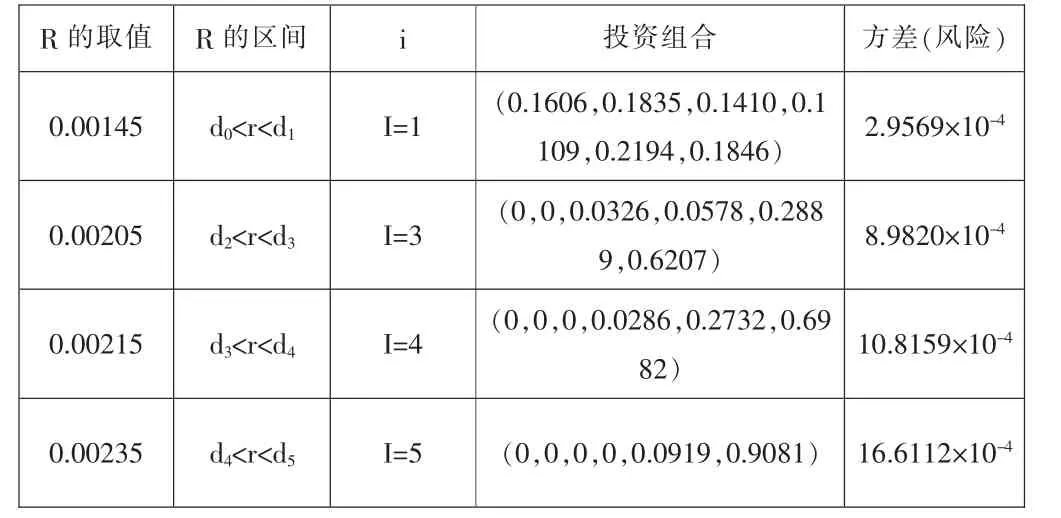
表3 ：模型（M2）的投资组合及风险的取值

2.Markowitz不相关资产模型的结果

同上面一样，把表格2中求得的数据代入（3）式，并运用风险的计算公式得到了以下结果：

表4 ：Markowitz不相关资产模型下投资组合及风险的取值

四、结论

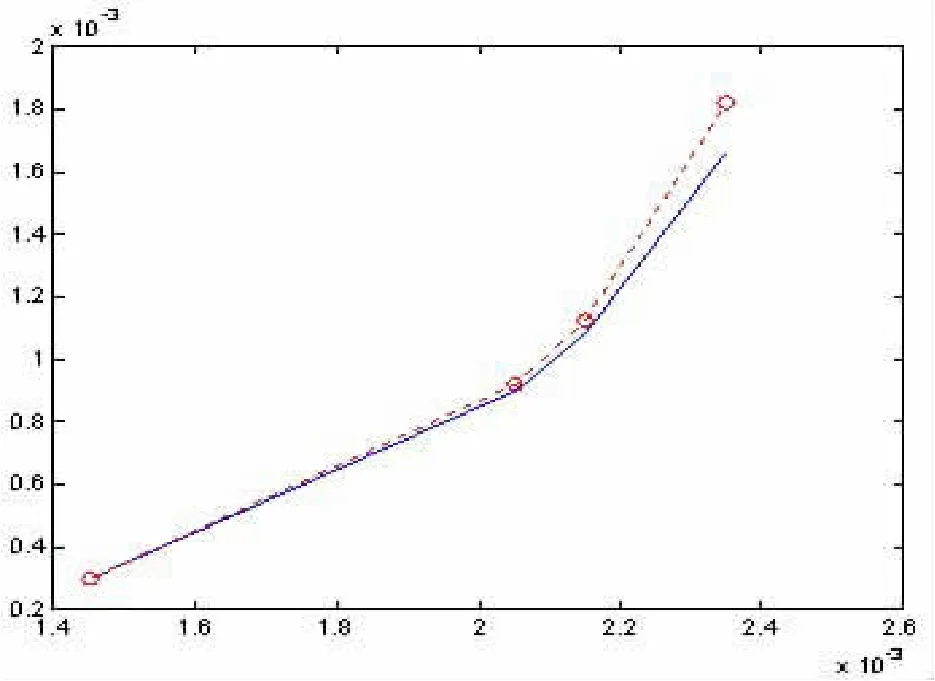
图1 两个模型风险的比较

从上图中风险的比较以及前一部分的计算结果中，我们可以得到以下结论：

1.我们从表3、表4的数据结果可以看出该模型的可行性及正确性。表3中投资比例的取值均为正数，且每组之和均为1。这验证了不允许卖空的条件：lTx=1及x叟0。

表4中投资比例的取值中有负数出现，这也符合Markowitz不相关资产模型中允许卖空的假设，同时也满足lTW=1。因此,我们选取的模型是正确且可行的。

2.在收益率的取值相同的条件下,当分别运用（3）、（4）式求出投资组合后，从表中我们可以看出在收益率相同的前提下,改进的不允许卖空条件下不相关资产投资模型比传统的Markowitz不相关资产模型产生的风险要小。这就说明,新的模型比传统的Markowitz不相关资产模型更有优越性。

3.从表3、表4的结果还可以看出：这一投资组合所产生的风险都非常小。这说明，不相关资产组合能产生更小的风险。也就是说，在实际操作中，投资者应当尽可能选取那些不同行业、不同种类的股票组合投资,这样相关系数低，有利于分散风险。[5]

致谢

在本文完成之际特别要感谢的是北京交通大学的张作泉教授。在撰写本文的过程中，他给予了极大的帮助和指导，在此表示衷心的感谢。

[1]Markowitz H.Portfolio selection[J].The Journal of Finance,1952,7(1): 77-91.

[2]Merton.An analytic derivation of the efficient frontier[J].Journal of Finance and Quantitative Analysis9,1972.1851-1872.

[3]李仲飞,汪寿阳.投资组合优化与无套利分析[M].北京:科学出版社, 2001,(5):73-76.

[4]陈剑利,诸葛莉,周明华.马克维兹模型在深圳股市应用中的实证研究[J].浙江工业大学学报,2005,(4):471-473.

[5]孙忠艳.分散化投资规模及风险资产比例选择的实证研究[J].重庆工商大学学报(社会科学版),2003,20(3):18-20.