谈如何将医学问题转化为数学问题

魏 杰，董

（兰州工业高等专科学校，甘肃 兰州 730050）

谈如何将医学问题转化为数学问题

（兰州工业高等专科学校，甘肃 兰州 730050）

对于医学中的大量实际问题，可通过分析和筛选，剔除次要因素，突出主要因素，做适当抽象和简化，将问题转化为数学问题，进而利用数学方法解决。

高等数学；数学模型；数学教学；医学

随着科学技术的发展和计算机的应用与普及，医学逐步由传统的定性描述阶段向定性、定量分析相结合的新阶段发展，即从能够有效探索医学科学领域中物质的量与量关系的规律性，向定量、精确、可计算、可预测、可控制的方向发展。而数学模型正是有助于医学家及生物学家将某些变量隔离出来、预测未来实验结果或推论无法测量的种种关系的强有力的工具。因此，数学模型及数学理论与方法在医学中的应用日益广泛和深入。最引人注目的是医疗诊断专家系统[1]及1974年丹麦免疫学家Niels K.Jerne在其论文《关于免疫系统的网络学说》中揭示的现代医学科研新模式：医学问题—数学化（定量分析）—数学模型—反馈修正（实践检验）—定性理论。还有一些作者在预防医学、基础医学和临床医学等传统学科试图建立数学模型和运用数学理论与方法来探索其数量规律[2]。

而目前大多数医学院校仅开设高等数学课程，并没有开设数学建模课程，使得数学教学内容与医学严重脱节，没有注意训练学生如何从实际医学问题中提炼出数学模型，以及如何将数学分析的结果用来解决实际问题，其结果是学生学了不少数学知识，但不会应用。所以高等数学作为医学院校的一门基础课程，应将数学建模思想渗透到教学内容中[3～6]。但由于高等数学的高度抽象性和严密逻辑性，往往会给学生的学习和教师的授课带来一定困难。为了使学生能更好地掌握这门课程并能用高等数学基础知识解决医学中的一些实际问题，正确理解和巩固所学知识，强化其应用数学解决实际问题的意识，我们结合一些具体的医学问题，分析和讨论数学模型方法的应用。

用数学方法解决医学问题的关键是如何将医学问题转化为数学问题，即如何在两者之间建立一座桥梁（建模）。我们根据多年的数学建模教学经验，分析、讨论如何建模并给出一些医学问题的数学模型。

1 如何将医学问题转化为数学问题

建立一个医学问题的数学模型，除需要必须的医学专业知识外，还需要一定的洞察力和想象力，以便筛选、剔除次要因素，突出主要因素，并作出适当的抽象和简化。全过程一般分为表述、求解、解释、验证几个阶段，通过这些阶段完成从现实对

象到数学模型、再从数学模型到现实对象的循环（见图1）。

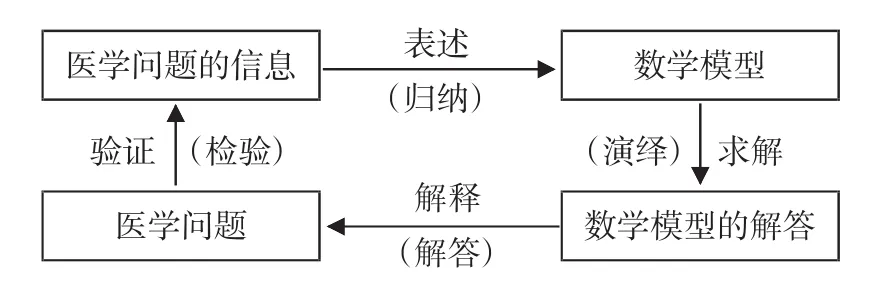
图1 医学问题建立数学模型流程

其中表述即将医学问题翻译成数学问题，用数学语言确切表达出来。这是一个关键的过程，需要对实际医学问题进行分析，甚至要调查研究，查找资料，对问题进行简化、假设、数学抽象，运用有关的数学概念、数学符号和数学表达式去表现医学对象及其关系。求解即选择恰当的方法，求得数学模型的解答。解释即为将数学解答用普通人能听懂的语言翻译为现实对象。最后通过实践验证解答的合理性。

由于医学问题的复杂性，建立数学模型不一定一次就能成功。一次建模不成功时，可以先剔除实际医学问题中的次要因素，建立比较简单的数学模型。然后逐次修改并逐渐强化条件，从而建立比较符合实际问题的数学模型。

2 模型实例

2.1 以血管中单位时间的血流量问题为例讨论如何将医学问题表述成数学问题

虽然血管呈现出一个不规则的几何形状，但其类似于圆柱体。首先在合理的假设下结合本问题所涉及到的专业知识建立一个粗略的模型，将血管看成一个圆柱形的管子去考虑。设其横截面的半径为R（cm），管中的血流平行于血管的中心轴。由于血管中血液在各点处的流速v是各点与血管中心距离r的函数，即v=v（r），故此时血流量等于流速乘以面积。而已知距离中心轴r处血的流速为：

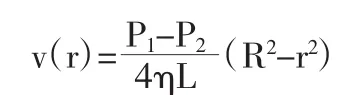
其中 η 为血液的粘滞系数，L 为血管长度，P1、P2（P1＞P2）为血管左、右端的血压。

然后求出单位时间内通过的血流量Q，但这只是粗略的近似值。那么如何才能得到精确的答案呢？联想到高等数学中在求不规则立体体积时使用的微元法，在取定的横截面任取一个内径为r，外径为r+dr（圆心在血管中心）的小圆环作为研究问题的微元（见图2），它的面积近似于2πrdr，在单位时间内，通过小环面的血流量dQ近似为：

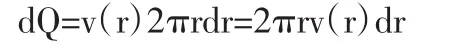
单位时间内通过该小环面的血流量为：

即为本问题的数学模型。

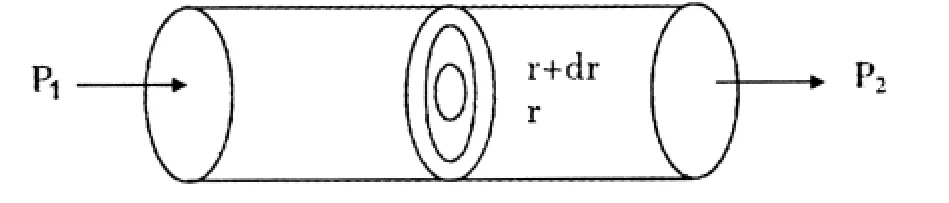
图2 血管中单位时间内血流量问题数学模型

2.2 以传染病模型[7]为例讨论如何由粗到细建模

传染病传播涉及的因素很多，如传染病患者的多少、易感人群的多少、传染率的大小、排除率的大小、人口的出生和死亡，以及人员的迁入和迁出、潜伏期的长短、预防疾病的宣传等因素的影响。如果一开始就把所有因素考虑在内，很难建立比较合理的数学模型，因此应先剔除众多次要因素，抓住主要因素，把问题简化，建立相应的数学模型；然后将所得结果与实际比较，找出问题，逐步修改原有假设，再建立一个与实际比较吻合的数学模型。

可大致通过以下4方面来考虑：描述传播过程，分析感染人数的变化，预报传染高峰时刻，制定相应的群体免疫与预防措施。传染的主体是人，传播是由于患者在被收治隔离前与其他人的传染接触而发生的，所以可通过对人群分类来建立数学模型分析传染病传播过程的一般规律，以达到预防与控制疾病的目的。

2.2.1 考虑最简单的情形（Malthus模型）设某地区共有n+1人，最初共有i人感染此病，t时刻已感染的患者数为i（t），假定每一已感染者在单位时间内将疾病传播给k个人（k称为该疾病的传染强度），且设此疾病既不导致死亡也不会康复，可导出：

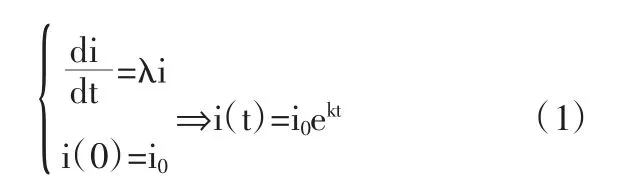
此模型即Malthus模型，它大体反映了传染病流行初期的患者增长情况，在医学上有一定的参考价值，但随着时间的推移，将越来越偏离实际情况。

原因在于已感染者与尚未感染者之间存在明显区别，有必要将人群划分为已感染者与尚未感染的易感染者，改进如下。

2.2.2 考虑SI模型设t时刻的患者数与易感染人数分别为i（t）与s（t），初始时刻的患者数为i0，根据患者不死亡也不会康复的假设，可得：

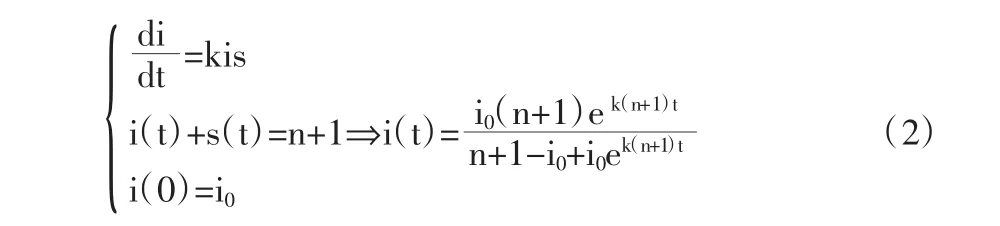
统计结果显示，（2）预报结果比（1）更接近实际情况。医学上称曲线为传染病曲线，由此模型可得出传染病的流行高峰值。此值与传染病的实际高峰期非常接近，可用作医学上的预报公式。但SI模型仍有不足之处，它无法解释医生发现的现象，且当时间趋于无穷时，模型预测最终所有人都将患病，与实际情况不符。为解释医生发现的现象，再次修改假设条件，建立新的数学模型。

2.2.3 考虑SIR模型 将人群划分为3类：易感染者、已感染者和已恢复者。分别记t时刻的3类人数为s（t）、（it）和 （rt），可得：

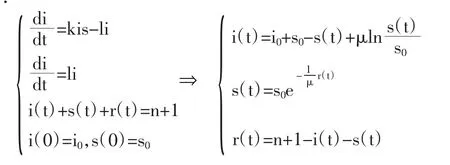
此外，根据2003年对SARS等传染病的认识，人群中可能还有疑似患者、潜伏期患者等。所以如果将人群分得更细，例如将人群分为：t时刻的易感染人数s（t），潜伏期人数 （it），疑似人数e（t），确诊人数p（t），治愈人数 （rt），可得下面更加精细的模型。

2.2.4 考虑GSIR模型

其中k为传染率，l为疑似率，r为治愈率，μ为死亡率，α为疑似病例中每天被排除的确定为健康的人数占疑似病例的比例，β为疑似病例中每天确诊的人数占疑似病例的比例，T为疾病的潜伏期，e为自由带菌者转为患者的日转化率，γ为自由带菌者中每天被发现疑似病例的比例。

通过不断深入研究，不仅能使学生对数学模型有较深入和全面的理解，还能使学生明白一个好的数学模型不是一次就能完成的，而是要通过不断实践、修改、校正才能逐步接近现实。另外，传染病模型还可以应用于人口增长模型、新产品的销售等。

总之，在医学数学教学过程中融入数学建模思想的同时，教会学生如何将实际医学问题利用数学方法转化为数学问题，进而逐步建立一个比较完善的数学模型，并通过对数学问题的解决从理论上说明实际医学问题，使学生对数学方法的运用产生兴趣，逐步提高医疗水平。另外，还应使教师转变教学观念，更新教学方法，使数学教学从与医学脱节的理论传授模式向医学实际的应用数学模式转变。

[1]易非易.论医学数学化[J].数学理论与应用，2001，21（4）：124～126.

[2]万志超，蒋善丽.对医学数学教学的探讨与思考[J].中国医学教育技术，2006，20（6）：462～463.

[3]蒋善丽，李兆强.医学高等专科学校数学教育改革初探[J].卫生职业教育，2007，25（6）：7～9.

[4]罗万春.医学高等数学中渗透数学建模的实验研究[J].卫生职业教育，2007，25（6）：5～7.

[5]黄平.提高医科高等数学课堂教学质量的几点体会[J].数理医药学杂志，2009，22（4）：503～504.

[6]韩明莲，卢书成.高等数学教学中渗透数学建模思想[J].数理医药学杂志，2006，19（5）：555～556.

[7]姜启源.数学建模[M].北京：高等教育出版社，2002.

G421

B

1671-1246（2010）03-0065-03

注：本文为甘肃省教育厅资助项目（0813B-01）