拟动力试验中改进的显式数值积分方法

王德才, 叶献国,2

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009;2.合肥工业大学 安徽土木工程结构与材料省级实验室,安徽 合肥230009)

0 引 言

拟动力试验方法作为目前结构抗震试验研究中应用广泛的一种试验方法,是将计算机与加载作动器联机进行求解结构动力方程的试验方法[1]。拟动力试验的主要部分之一是进行结构动力方程求解计算,数值积分方法直接影响计算过程的稳定性和试验误差的大小,所以数值积分方法的选择对于整个试验起着至关重要的作用。积分方法主要分为显式方法和隐式方法,在选择时主要考虑其稳定性、精度与误差累积特性等。

显式方法主要有线性加速度法、中央差分法、显式Newmark法(NEM)和修正Newmark法等,这些方法计算效率高且不需要迭代求解,但都是有稳定条件的。为了满足稳定条件,当结构有高阶振型存在时,必须选取很小的时间步长才能满足稳定性要求,这将增加试验的持续时间并且会导致累积误差增大,也限制了一些结构进行拟动力试验。同时对于任何试验来说试验误差是不可避免的,要取得准确的试验结果就需要将试验误差控制在一定范围以内。为了解决显式积分方法条件稳定的缺点,许多研究人员又对无条件稳定的隐式积分方法进行了研究[2—5],但是采用隐式方法需要进行迭代校正达到收敛解,这不但需要整个试验系统联机迭代实现,而且在每个时间步长中导入了不希望的卸载滞回效应。为了克服显式方法和隐式方法固有的缺点,文献[6-9]提出了无条件稳定显式算法(UEM),其数值特性等同于常加速度法,不具有数值耗散作用。

本文结合了NEM算法和UEM算法的特点,并在算法中引入数值耗散系数,改善了传统显式积分方法所固有的一些缺陷。本文提出的改进的显式积分方法,通过对3个参数的选择,可以实现显式积分的无条件稳定或具有数值耗散,可以根据试验结构的特点选择参数,从而得到准确的试验结果,同时使试验误差降低到最小。

1 改进的显式数值积分方法描述

设时间步长为Δt,则在某一时刻ti+1的离散时间动力方程为:

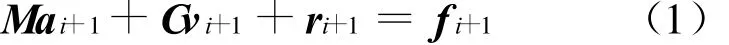
改进的显式积分方法对位移和速度分别作了以下假定:

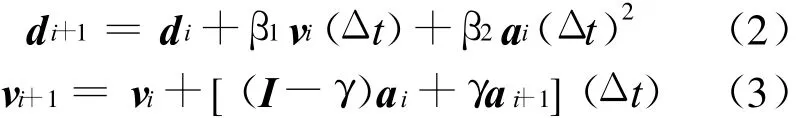
分别按照UEM 算法[6]和NEM 算法对β1和β2进行以下2组定义。

第1组(按UEM 算法):

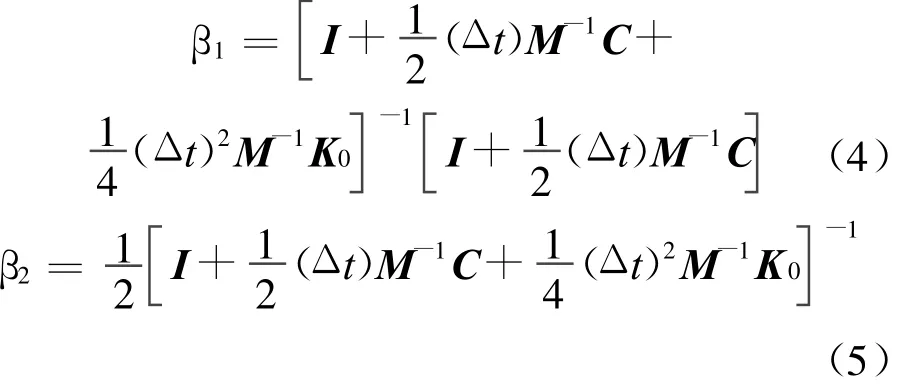
第2组(按NEM 算法):

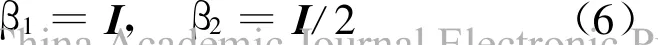
其中,K0为初始刚度矩阵。

系数矩阵γ的定义与文献[10]相同,即

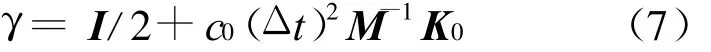
其中,系数c0是大于或等于0的常数,在实际的应用中根据需要的数值耗散能力选取 c0的值。一般c0的取值,对于第1组小于0.12即能满足要求,对于第2组,文献[10]对其数值特性作了相应的讨论,认为小于0.15即能满足要求。

2 算法特性

2.1 算法的稳定性

研究数值积分方法的数值特征,一般采用无阻尼单自由度线弹性结构进行简化分析[6]。对于改进的显式数值积分方法,其算法可以写成如下递推矩阵的形式:

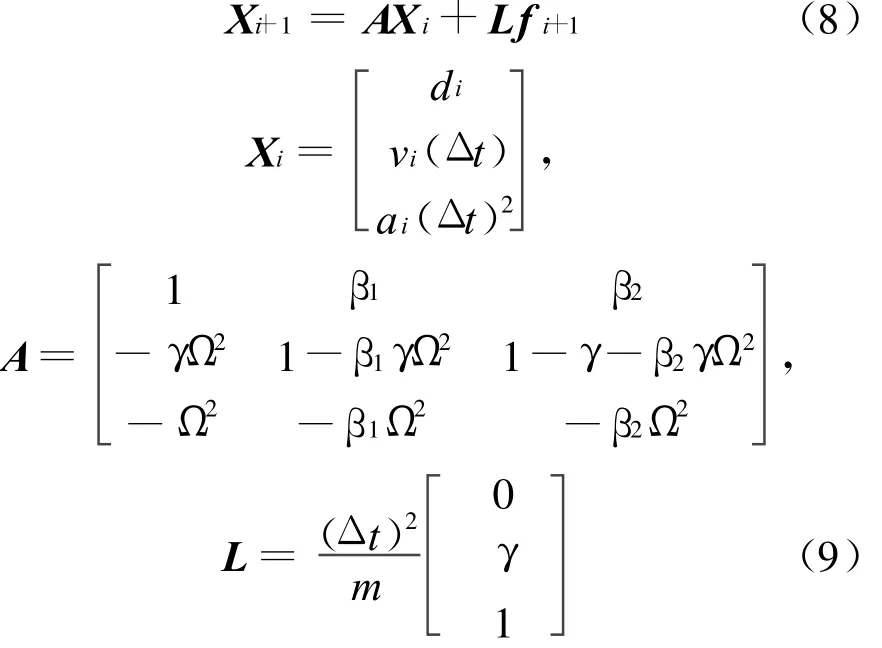
其中,A称为放大矩阵;L称为载荷算子;Ω=ω(Δt)。矩阵A的特征方程为:

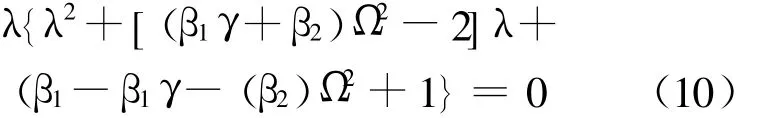
在(10)式中 β1和 β2按照不同的定义,得到的特征多项式是不同的,分别如下:

第1组:

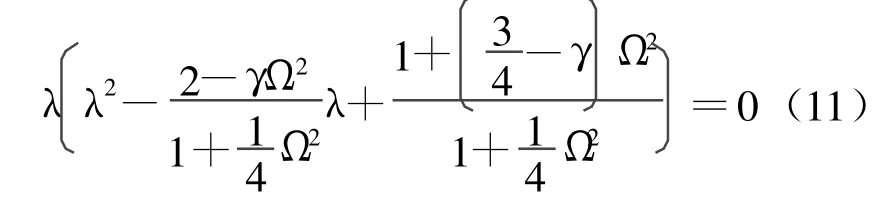
第2组:

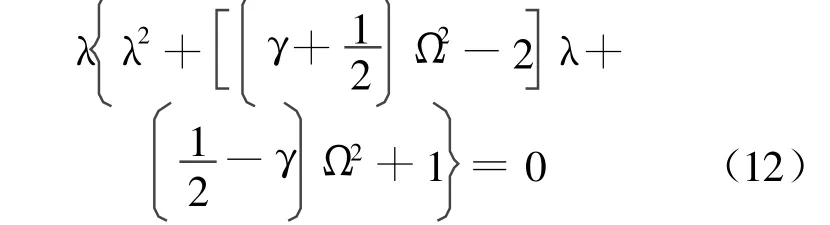
当c0=0,即 γ=1/2时,从(11)式可以看出其特征多项式与常平均加速度法相同,这时改进的方法成为 UEM算法,具有无条件稳定特性并且具有二阶精度。从(12)式可以看出其特征多项式等同于NEM 算法,改进的方法成为NEM算法。从(11)式、(12)式可以求出:

从(11)式、(12)式可以得到a和b的表达式;当矩阵A的谱半径ρ(A)≤1.0和 λ1,2为共轭复数时,算法才是稳定的,则要求b≥0且(a2+b2)1/2≤1.0,由此可得相应的稳定条件;由于γ=1/2+c0Ω2≥1/2,所以稳定条件中的稳定下限自动满足。对于稳定上限,将γ=1/2+c0Ω2代入稳定条件不等式中,从而得到稳定上限不等式。

a,b的表达式、稳定条件及稳定上限 Ωu表达式见表1所列。

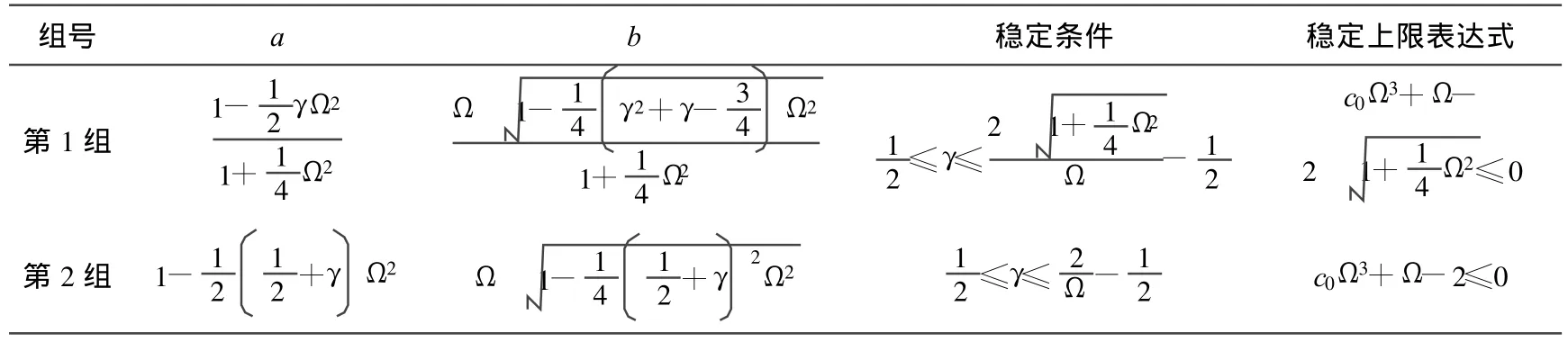
表1 a、b稳定条件及稳定上限表达式

将稳定上限表达式的数值解绘制成图,如图1所示,可以得到随c0取值的不同,Ω的稳定上限 Ωu的变化。

从图1中可以看出当c0从0增加到4.0时,第1组的稳定上限从∞降到0.7,而第2组的稳定上限从2降到0.68,所以采用第1组比第2组有更大的稳定范围。在实际应用中对于第1组选择的c0值,一般小于0.12即能满足数值耗散的要求,此时对应的稳定上限大于1.8。对于第2组选择的c0值,一般小于0.15即能满足数值耗散的要求,此时对应的稳定上限大于1.5。显然,当c0=0时,对于第1组成为UEM 算法,对应的为无条件稳定。而对于第2组则成为NEM算法,对应的稳定范围为0≤Ω≤2。

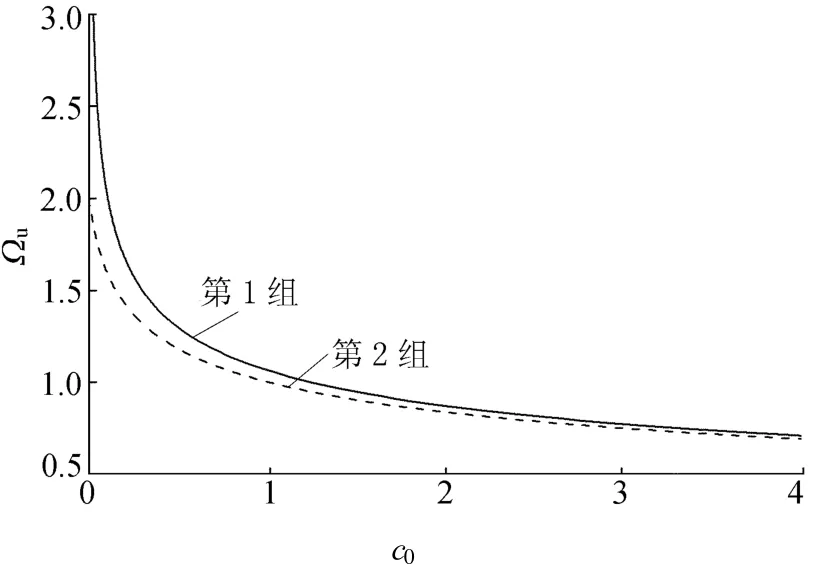
图1 改进显式积分方法的稳定上限

2.2 周期失真与数值耗散

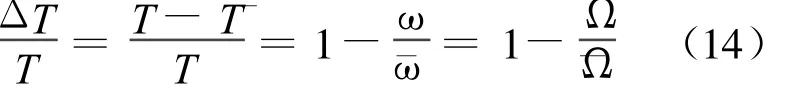
其中,¯Ω=arctan(b/a),¯ω=¯Ω/(Δt)为数值解法的失

周期失真率的表达式为:真频率;¯T=2π/¯ω为失真周期 ;T=2π/ω为 真实周期。

数值阻尼比¯ξ的表达式为:

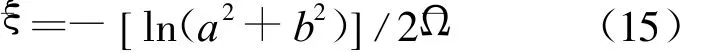
2组周期失真率和数值耗散阻尼比与 Ω之间的关系如图2和图3所示。

图2 周期失真率的变化

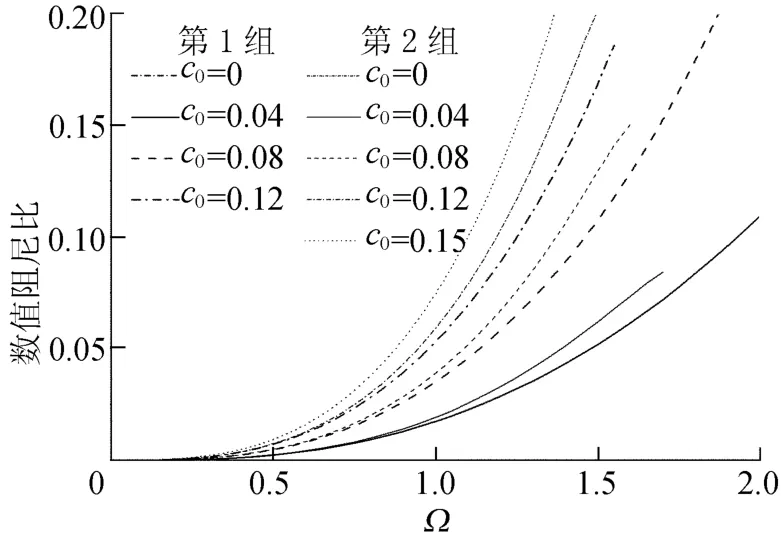
图3 数值阻尼比的变化

从图2、图3可以看出,对于给定的 Ω,当c0值增加时,采用第1组系数假定其周期失真率不断减小,而采用第2组系数假定时其周期失真率不断增加;2组的数值阻尼比都随着c0的增加不断增加;更大的数值阻尼比基本上对应着更高的周期失真率。

当c0=0时,第1组系数假定成为UEM算法,具有最大的周期失真率且数值阻尼比为0,第2组系数假定成为NEM算法,具有最小的周期失真率且数值阻尼比为0;当选取c0＞0时,无论是第1组系数假定还是第2组系数假定,在 Ω＜0.6时,数值阻尼比的变化并不快,但当Ω＞0.6时数值阻尼比迅速增长,这表明试验结构的高阶振型的影响能被很好地过滤掉,而低阶振型能被准确计算。

2.3 误差传播与累积特性

拟动力试验过程中,由于位移控制误差的存在,计算的位移并不能精确地施加到试件上,这样测得的恢复力必然是不精确的,同时对恢复力的测量及反馈也存在误差。这些误差都将影响每一步的计算结果,所以需要进行误差传播特性的研究。

误差传播特性分析主要通过位移反馈误差放大因子和恢复力反馈误差放大因子2个指标衡量误差传播与累积特性[11],文献[12]对位移和恢复力误差放大因子的含义作了较为详细的解释,放大因子越大表示结果受到试验误差的影响越大。通过推导得出了2组算法的位移和恢复力误差放大因子,假定为第i步位移反馈误差放大因子,为第i步恢复力反馈误差放大因子。对于第1组:

对于第2组:

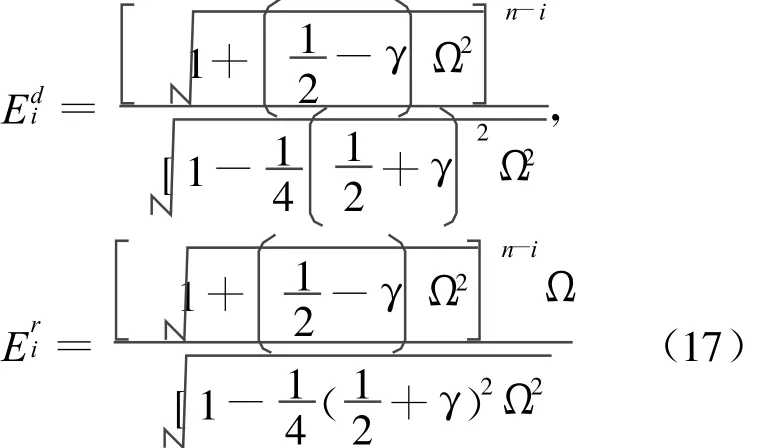
UEM算法:

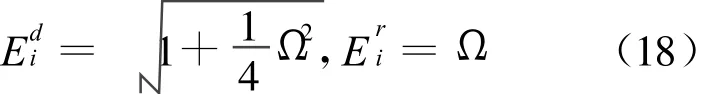
NEM算法:

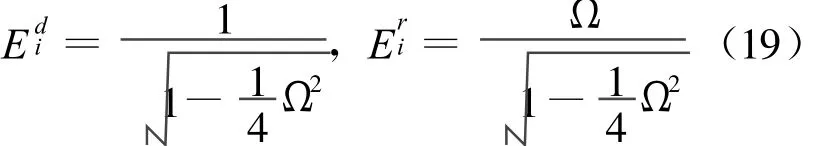
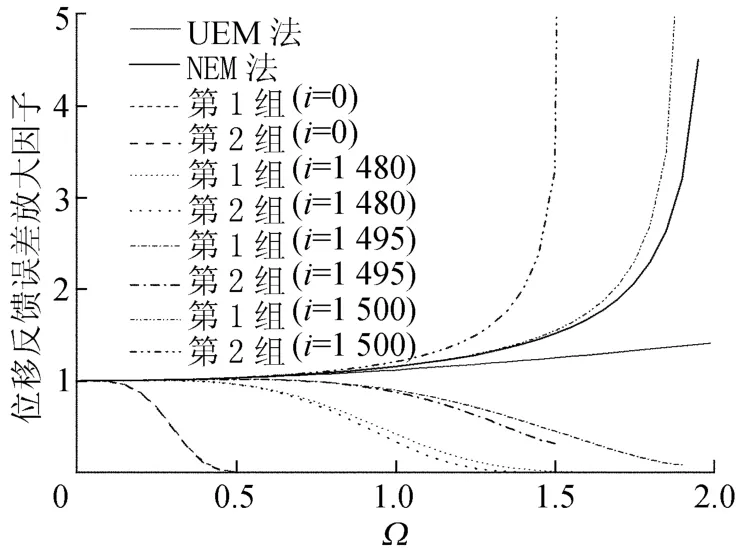
图4 位移反馈误差放大因子对比

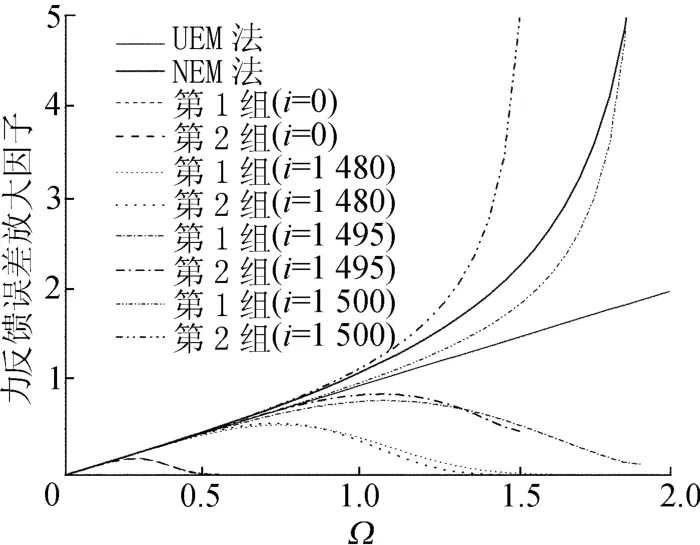
图5 恢复力反馈误差放大因子对比

从(18)式、(19)式可以看出,2种方法跟时间步总数n及指定的时间步i没有关系,这是由于它们的谱半径ρ(A)≡1.0,关系曲线也分别绘于图中。其它情形下c0取值为1.2,时间步总数n取为1 500步。

从图4、图5可以看出,UEM 法的位移和力误差放大因子明显小于NEM法,所以前者的误差传播特性要好于后者;当c0取值大于0时,i取0～1 495,其误差放大因子都明显小于c0=0的情况,误差放大因子都呈现先增加然后减小直至为0,只有i=1 500时大于c0=0的情况,所以通过引入系数c0明显改善了UEM法和NEM法的误差传播特性,并且具有数值耗散特性。

按照第1组系数定义时,其误差传播特性在i=1 500时明显好于按第2组系数定义时的误差传播特性,但当i≤1 495时相差不大;由此可以得出,系数c0的引入不但使数值积分方法具有数值耗散特性,而且其误差传播特性优于 UEM法和NEM法。

3 数值模拟计算

编制相应的计算程序,通过以下算例验证改进的显式积分方法的稳定性、数值耗散特性及误差传播与累积特性。采用一个双自由度剪切型结构,底层质量m1=1.5 kg,顶层质量m2=10 kg,每一层刚度均为4 000 N/m,结构处于弹性状态,采用常用的Kobe(EW)地震波,峰值加速度调整为0.2g,每步时间间隔 Δt=0.02 s,系数c0取0.1。每步的试验位移误差采用均值为0、标准差为0.05的正态分布随机数。

由已知条件可以得到结构的自振频率分别为13.88 rad/s和74.44 rad/s,对应振型分别为:

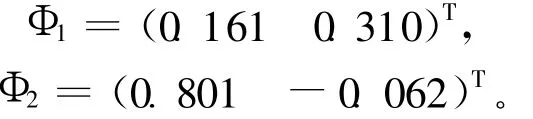
计算结果显示取c0=0,即采用NEM法和UEM法结构顶层位移反应都能较好地被计算,而底层位移反应则不能被准确计算。

图6所示绘制了不同方法计算的前10 s底层位移反应曲线,从中可以看出在UEM法中引入模拟误差,结构底层的位移反应曲线出现高频振荡,随着误差的累积出现反应的紊乱无序,而取合适的c0值却能得到稳定可靠的数值解。以上现象是由于以下几个原因:

(1)一阶振型对应的Ω1=0.278 rad,由于其值很小,所以不论c0等于0还是大于0,周期失真率及力与位移误差放大因子都很小。而二阶振型对应的 Ω2=1.489 rad,此时周期失真比较严重,并且UEM法在二阶振型下对应的力和位移误差放大因子也较大,从而也具有较为严重的误差累积。

(2)UEM法不具有任何的数值阻尼。

(3)尽管结构各层的位移反应主要由一阶振型控制,二阶振型的贡献并不明显,但从二阶振型的比例关系(0.801/-0.062=-12.92)可以明显地看出,二阶振型对底层的影响要远大于对顶层的影响。如果误差在二阶振型被传播和累积,就会导致二阶振型存在严重的虚假增长,尽管跟一阶振型反应相比,二阶振型对结构的贡献并不大,但是对结构底层还是会产生较大的影响,从而无法得到底层的准确位移,所以顶层位移一般能较准确地得到,而底层位移时程曲线会呈现出紊乱状态。

当c0＞0时,顶层和底层位移均能得到准确的结果,是由于此时具有较好的抑制高阶振型的虚假增长,并且能对低阶振型进行准确积分,对高频的影响能很快耗散。所以较好的误差传播特性和数值阻尼的耗散作用,是有效抑制高阶振型影响的主要原因。

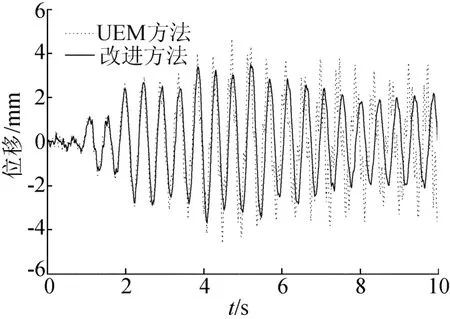
图6 采用不同方法底层位移反应

4 结 论

提出的改进的显式数值积分方法可以通过3个参数的选择实现不同的需求,包括目前应用较多的NEM法和显式无条件稳定的UEM法。对于简单的结构可以选择NEM法,此时对位移假定的参数选择与NEM法相同,数值耗散系数选择为0,这样就可以不用通过静力试验测定试件的初始刚度。

当显式积分方法稳定性不满足而需要将积分时间间隔减小很多时,可以使用UEM法,此时对位移假定的参数选择与UEM法相同,数值耗散系数选择为0,同时需要通过静力试验测定试件的初始刚度。当在试验中存在高频振荡的影响时,对位移假定采用UEM法,同时对速度的假定中选择一个适当的耗散系数,此时不但具有数值耗散特性,而且具有较好的误差传播和累积特性。

所以,改进的显式积分方法比其它显式积分方法具有更广泛的适用范围,消除了普通的显式数值积分方法的固有缺陷。

[1] 邱法维,钱稼茹,陈志鹏.结构抗震试验方法[M].北京:科学出版社,2000:3-6.

[2] Bonelli A,Bursi O S.Generalized-αmethods for seismic structural testing[J].Earthquake Engineering and Structural Dynamics,2004,33:1067-1102.

[3] 王焕定,陈再现,王凤来,等.高阶单步拟动力试验算法[J].工程力学,2008,25(11):14-19.

[4] Bursi O S,Shing P B.Evaluation of some implicit timestepping algorithms for pseudodynamic tests[J].Earthquake Engineering and Structural Dynamics, 1996,25:333-355.

[5] 邱法维.采用隐式积分方法和子结构技术的拟动力实验[J].土木工程学报,1997,30(2):27-33.

[6] Chang S Y.Explicit pseudodynamic algorithm with unconditional stability[J].Journal of Engineering Mechanics,2002,128(9):935-947.

[7] Chang S Y.Improved numerical dissipation for explicit methods in pseudodynamic tests[J].Earthquake Engineering and Structural Dynamics,1997,26:917-929.

[8] Chang S Y,Tsai K C,Chen K C.Improved time integration for pseudodynamic tests[J].Earthquake Engineering and Structural Dynamics,1998,27:711-730.

[9] Chang S Y.An explicit method with improved stability property[J].International Journal for Numerical Methods in Engineering,2009,77:1100-1120.

[10] Chang S Y.The γ-function pseudodynamic alg orithm[J].Journal of Earthquake Engineering,2000,4(3):303-320.

[11] Chang S Y.Error propagation of HHT-αmethod for pseudodynamic tests[J].Journal of Earthquake Engineering,2005,9(2):223-246.

[12] 王德才.拟动力试验数值积分方法及子结构拟动力试验研究[D].合肥:合肥工业大学土木与水利工程学院,2007.