两段法渗碳工艺参数的优化设计系统

李 云, 陈小丽, 吴玉程

(合肥工业大学材料科学与工程学院,安徽合肥 230009)

随着电子计算机技术的不断发展和市场经济体制的逐步建立与完善,热处理行业出现了一系列新的观念:跟踪并采用国际先进技术的全局观念;立足于自动化的质量观念;寓节能于自动化的观念。在这种背景下,如动态仿真模拟、数值程序控制、优化设计、模糊控制及专家系统等一系列新技术应运而生,并广泛应用于各个热处理场合。就钢件气体渗碳而言,有关它的动态控制等计算机辅助设计的研究不少,但大都依赖于扩散方程的数值解,而从精确的数学模型出发进行优化设计渗碳工艺参数的研究并不多见,究其原因如下:钢件气体渗碳尤其两段渗碳是一个相当复杂的多相化学反应与扩散过程,渗碳后的碳含量分布受到多种因素的影响,因而建立一个高控制精度低能耗的数学模型比较困难。数值解法虽能解决上述问题,但却不利于在中小型工厂推广。

考虑到我国热处理行业中小型工厂较大型工厂多,普通渗碳较精密渗碳多的现状,本文选择了较为精确的两段法渗碳扩散方程的解析解[1],据此建立了一个包含7个变量与10个约束条件的数学模型,采用D-H伸缩保值法,以保证约束被破坏限度的容许标准来实现优化计算,运用Turbo C与FoxPro编程,计算出了一系列优化工艺参数,并将之收录到可进行增、删、改、查等功能的数据库档案中,进行了回归与曲线模拟,形成了一个较为完善的软件系统。该系统运算速度快、性能价格比高、人机界面友好,既利于在中小型工厂推广使用,又能作为热处理专家系统或综合数据库的组成部分在大型工厂或集成工作站上应用。

1 优化模型

1.1 两段法渗碳扩散方程的解析解

由扩散过程的Fick定律及第1类边界条件,可建立方程:

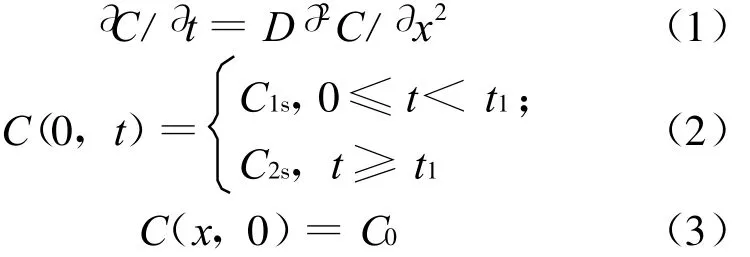
其中,C(x,t)为t时刻距扩散表面距离为x处的碳含量;D为扩散系数;x为渗层深度;t为渗碳时间为强渗期碳势为扩散期碳势;为钢件原始碳含量。

假设扩散系数D在渗碳过程中保持不变[2],则求解(1)～(3)式,渗碳工件内任何时刻、任何位置处的碳含量可由欧拉余误差函数来表达[1],即:

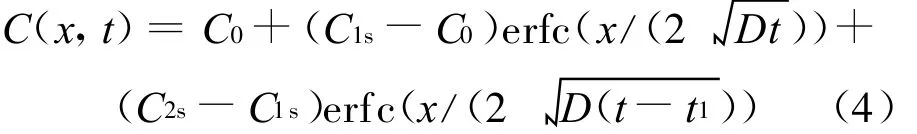
1.2 优化思路

1.2.1 实际技术问题

在实际生产中为了加快渗碳速度,通常采用两段渗碳工艺即强渗-扩散工艺,衡量工艺的优劣通常从以下2个方面考虑:

(1)渗碳质量的稳定性及可控性。包括要求达到的工件渗碳表面碳含量、要求达到的渗层深度S(常以有效硬化层深度的值来表征)、平缓的碳含量分布。

(2)渗碳时间t。从提高生产效率和节约能源着眼,要求渗碳总时间t最短。

1.2.2 优化思路及相关常量

(1)渗碳温度T。强渗期和扩散期采用同一温度,温度为920～950℃,用户可根据实际情况自行选取。

(2)扩散系数D。当渗碳钢件中w(C)＜1%,扩散系数D随碳质量分数的变化不是很大。一般的渗碳件中碳质量分数均低于1%,只有表层附近碳质量分数为1%左右,所以用平均扩散系数D来表示,并将D看作一常数,不会引起太大的误差。文献[3]给出D的计算公式:

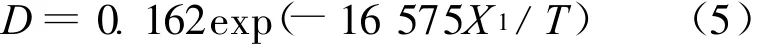
用户可根据(5)式,将所确定的温度 T代入计算D值。

(3)钢件原始碳含量C0由用户根据渗碳工件确定。

(4)优化思路。对于强渗-扩散渗碳过程,工艺参数应包括每阶段的温度、碳势、时间等6个参数。本文将两段温度取相同定值,提出渗碳总时间t,扩散时间由渗碳总时间t与强渗期时间的差值(t-)表示,这样便有强渗期碳势、扩散期碳势C2s、渗碳总时间t、强渗期时间t14个工艺参数。为此,假设有一个四维空间,在该空间内的任一点,它的4个坐标值x1、x2、x3、x4分别代表4个工艺参数,即四维空间中的一个点代表一组渗碳工艺,在工艺参数定义域范围内的整个空间代表了所有可能的两段渗碳热处理工艺。

所谓最佳工艺参数就是要在四维空间找出1个点,即1组工艺参数,使得渗碳层能达到技术要求,并且总的渗碳时间最短。为此,以总的渗碳时间作为目标函数,在工艺参数满足一些不等式约束条件下,对目标函数进行极小化求解。需要指出的是,如果等式约束的数目小于工艺参数的数目,满足等式约束的工艺参数不是唯一的,或者说在四维空间工艺参数定义域范围内,满足不超过4个等式约束条件的空间子集包括1个以上空间点。在这个子集内求出目标函数最小的1个空间点或1组工艺参数,即为所需要的最佳工艺参数。在计算中,采用了P-H伸缩保差法,它是在用于无约束求极值的N-M单形直接法的基础上,采用保证约束被破坏限度的容许标准来实现的。

1.3 约束条件

1.3.1 边界约束及变量步长

(1)有效硬化层深度Sl的范围及步长。采用有限元法计算渗碳工件(如齿轮)的接触应力,按判据能可靠地确定有效硬化层深度,考虑到模型的普适性,取0.6 mm ≤Sl≤1.8 mm,容许限度±0.1 mm,步长值为0.2 mm。

(2)渗层深度S的范围及步长。渗层深度S值由用户根据渗碳质量要求定出,但需满足大于或等于表面碳含量Ce对应深度C0,即:G1=S-S0≥0;不必超过有效硬化层深度Sl的最大容许值Sl+0.1,即=+0.1-S ≥0。

(3)强渗期碳势C1s的范围及步长。强渗阶段的碳势主要由温度决定,即主要取决于该温度下奥氏体的饱和碳质量分数,对碳钢由下式计算[4]:对合金钢则应修正如下:

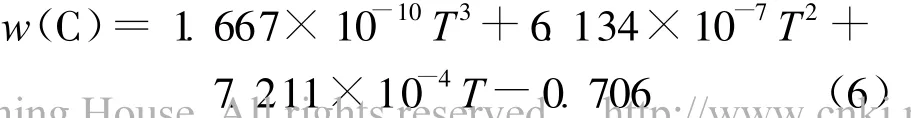
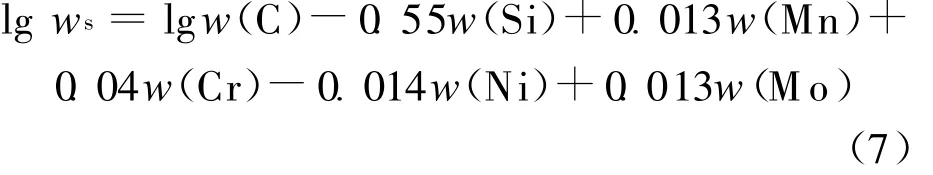
经计算并结合一定经验数据,取 C1s的范围为0.8%～1.3%,考虑到实际生产中碳势的测控精度,取其步长值为0.1%,则有:

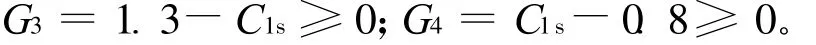
(4)扩散期碳势C2s范围及步长。两段气体渗碳进入扩散期后,气氛一般保持在相当于最终要求的表面含碳量,由此确定C2s的范围为:0.4%≤C2s≤0.9%,步长值为 0.1%,即:

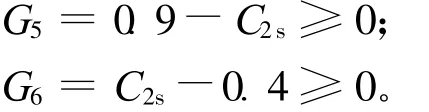
(5)渗碳总时间t及强渗时间t1的步长。实践证明,在平均碳势气氛中,当渗碳15 min后,渗层深变化约为±0.1 mm。该值在S的容许限度内,因而选取15 min作为t及t1的步长值,并以15 min作为 t1的初值,30 min作为 t的初值,t与t1间应满足:G7=t-t1≥0。

1.3.2 性能约束

(1)碳含量分布。由两段法渗碳的含量分布方程,碳含量满足如下等式约束:

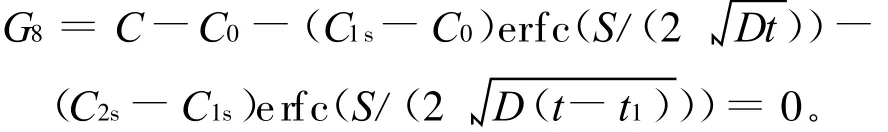
(2)表面碳含量Ce及有效硬化层碳含量R。渗碳处理的一个重要技术要求是表面碳含量Ce,该含量对应的渗层深度记作S0,由于工件渗碳后表层将不可避免地有一层氧化黑皮,其存在将影响工件的表面装配精度,增大接触应力,甚至引起机械故障,故要求在后续工序中将之磨削或进行抛丸处理,通常加工余量为0.125 mm,因而Ce便是指工件距表面0.125 mm处碳含量,即S0=0.125 mm,依据相关文献[5],Ce的取值范围为0.8%～0.9%。

当确定有效硬化层深度Sl的值后,结合上述约束条件,可得到数学模型如图1所示,当渗碳后碳含量分布曲线处于G9和G102条斜线框内时,便达到了质量控制要求,所以有:

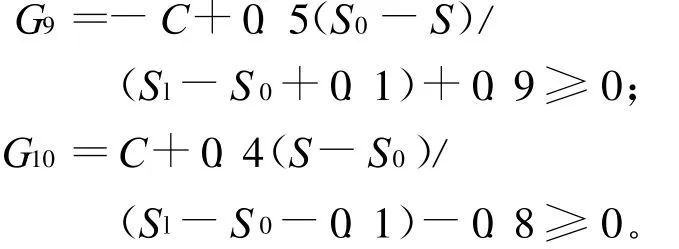
应当指出的是,要获得理想的碳含量分布,仅用表面碳含量Ce和规定深度的碳含量C来表征是不够的,本文在规定S步长为0.2 mm的情况下,即使对于S1的最小值0.6 mm,也有0.125、0.325、0.525 mm 3点,Sl越大,则控制点越多,计算所得碳含量分布曲线是相当精确的。

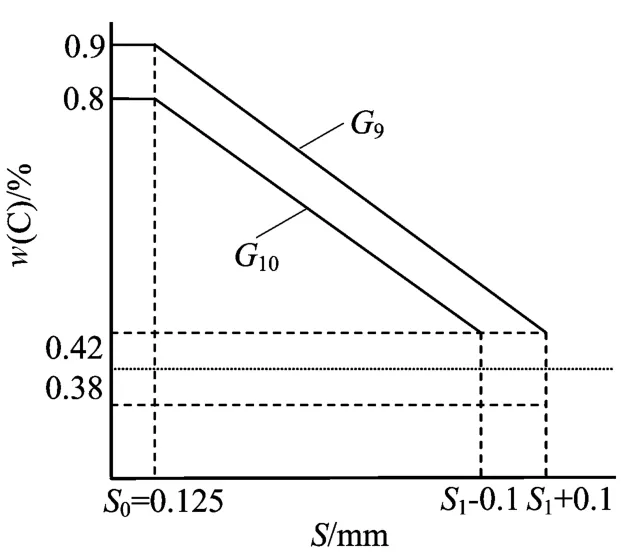
图1 数学模型示意图

有效硬化层深的碳含量设计关键在于过渡区碳含量的设计,即确定过渡区能达到550 HVc,即52.5 H Rc所需最低含碳量R(也称参考含碳量),R可以通过渗碳层的端淬曲线带确定,对于不同材料,有不同的参考含碳量近似数学表达式,故R取值范围为0.38%～0.42%。

2 软件系统

2.1 总体概貌

软件采用模块化结构,如图2所示。

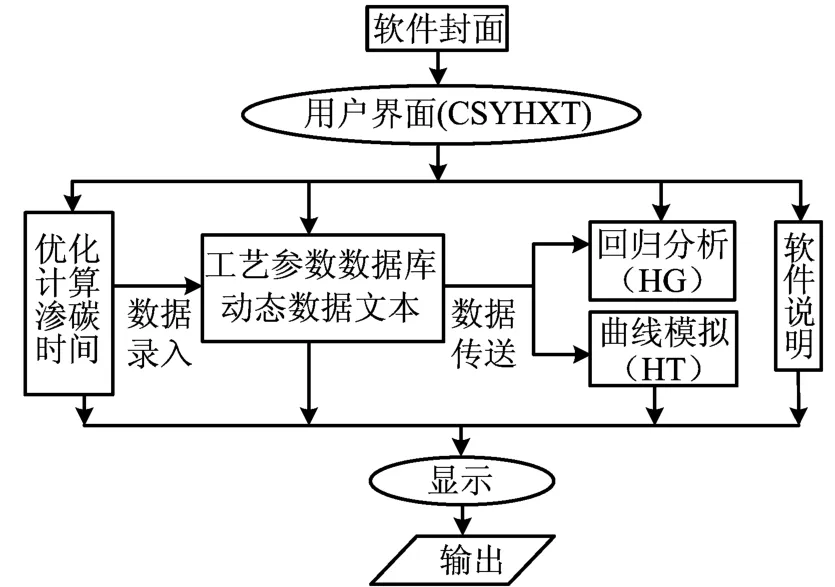
图2 优化软件系统流程图

系统主要特点有:

(1)CSYHXT用于两段法气体渗碳工艺参数的优化设计,在科学计算的基础上进行回归分析及碳含量分布曲线模拟。各模块之间通过数据库的中间数据文本进行数据的传递,因而各模块之间并不相互连接,可以独立开发,并能采用不同的程序设计语言(本系统采用 Turbo C和Fox-Pro)。这种软件系统的设计方法有利于加速软件的开发,便于维护和发展[6-8]。

(2)CSYHXT在Foxpro2.5B平台上开发,设计了友好的用户界面,在用户界面上一目了然地反映出系统的功能,如图3所示。用户根据图示用鼠标进行操作,十分简便。

(3)该系统运算速度快、可靠性高、容错能力强。在硬件配置要求并不算高的情况下,为本系统的大规模推广创造了条件。

2.2 优化计算

利用前面建立的数学模型,可进行渗碳总时间的优化汁算。下面为用优化计算渗碳时间程序获得的部分数据,Si=0.6,0.8,1.0,1.2,1.4,1.6,1.8 mm时相应的工艺参数见表1和表2所列,表中仅列出部分数据。

将表2中的数据与热处理手册提供的工艺参数数据比较,可得出使用优化后的工艺,渗碳周期缩短约15%～20%。

通常所说的强渗及扩散阶段的划分是相对于渗碳“净周期”而言的,传统的强渗-扩散实际应为5段:升温阶段、建立炉气碳势阶段、自适应控制强渗阶段、前期扩散阶段及后期扩散阶段。由于升温阶段和建立炉气碳势阶段对渗碳的贡献很少,可以不予考虑。因而,表中所列出的t、t1、t2是针对“净周期”而言,不包括升温阶段和建立炉气碳势阶段。

表1 优化所得数据(数据档案)

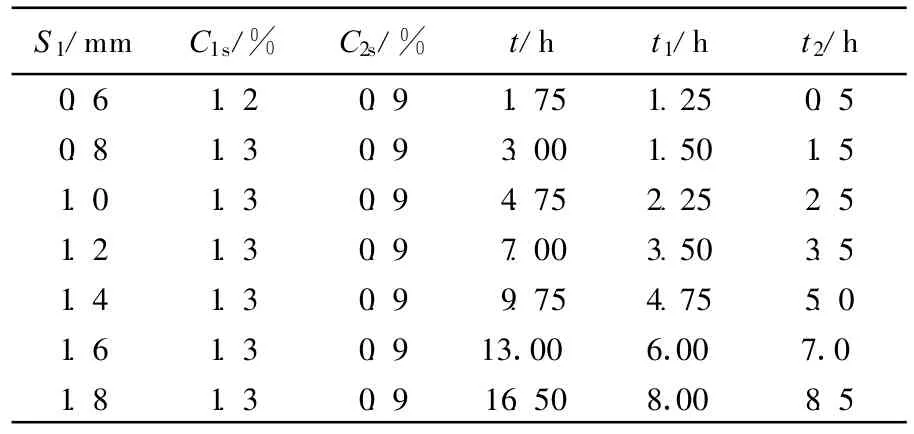
表2 优化计算所得工艺参数(参数档案)

2.3 数据档案

DBF采用二维表结构定义,具体建库方法参照FoxBASE+[8]或FoxPro。数据档案子系统包含以下功能:①菜单选择、功能键处理;②记录的追加、删除、修改、索引等维护以及查询、制表打印;③退出。

如查询有效硬化层深度Sl为0.8 mm,渗层深度S为0.525 mm时的工艺参数,进入 CSYHXT用鼠标选择“数据档案”中的“查询”,屏幕提示输入硬化层深度值0.8及渗层深度值0.525。如库中有其对应记录,屏幕将用表格形式显示出对应工艺参数。

渗碳时由高温奥氏体直接析出的碳化物一般沿晶界析出并逐渐长大,不易在晶内形成针片状。但在高碳势长时间强渗时,便会形成很难消除的魏氏型碳化物。因此,强渗时间tl不宜过长,使工作表面形成一个含有大量弥散颗粒状碳化物的高碳层,随后碳势下调至正常水平。这是工艺优化设计不可忽略的。

2.4 曲线模拟

在数据档案子系统下,用户只能看到大量数据组成的二维表结构,不利于直观地把握优化后的工艺结果。为此,编制了碳含量分布曲线绘制程序,将整个工艺过程中含量分布曲线显示在屏幕上。在渗碳之前预测渗碳的结果,以便事先了解能否达到工作设计的要求。这样本系统就可以发挥高效的“生产性试验设备”的功能。使人们在短时间内获得大量有关工艺参数对渗碳结果的影响信息,从而为实现优化工艺方案的计算机辅助设计(如实时控制)提供可能。

2.5 软件说明

软件说明子系统可以给用户使用软件提供帮助,以文本文件的格式于屏幕显示,其主要内容如下:

(1)本系统适用的工作平台是FoxPro 2.5B及更高版本,用户进入工作平台后,键入domain,回车便可。

(2)运行前请先装入UCDOS并运行特显模块;C:＞UCDOS;C:＞TX。

(3)本系统适用于常用渗碳材料20CrMnTi、20CrMnMo、20CrNi4等,在综合相关文献的基础上确定各参数的取值范围及步长。

(4)在优化计算模块中,最大值的设定目的是便于循环控制,减轻工作量。

2.6 退出系统

退出子系统提供了系统工作平台FoxPro到MS-DOS工作方式的出口。

2.7 试验数据

20#试样尺寸12 mm×12 mm×50 mm一对侧面防渗处理,在RJJ-90气体渗碳炉中930℃渗碳后空冷,CMT5.3B氧探头碳势测控仪测控碳势;试样平磨,在DV-4直读光谱仪测定3点平均渗碳层碳含量的数据见表3所列。

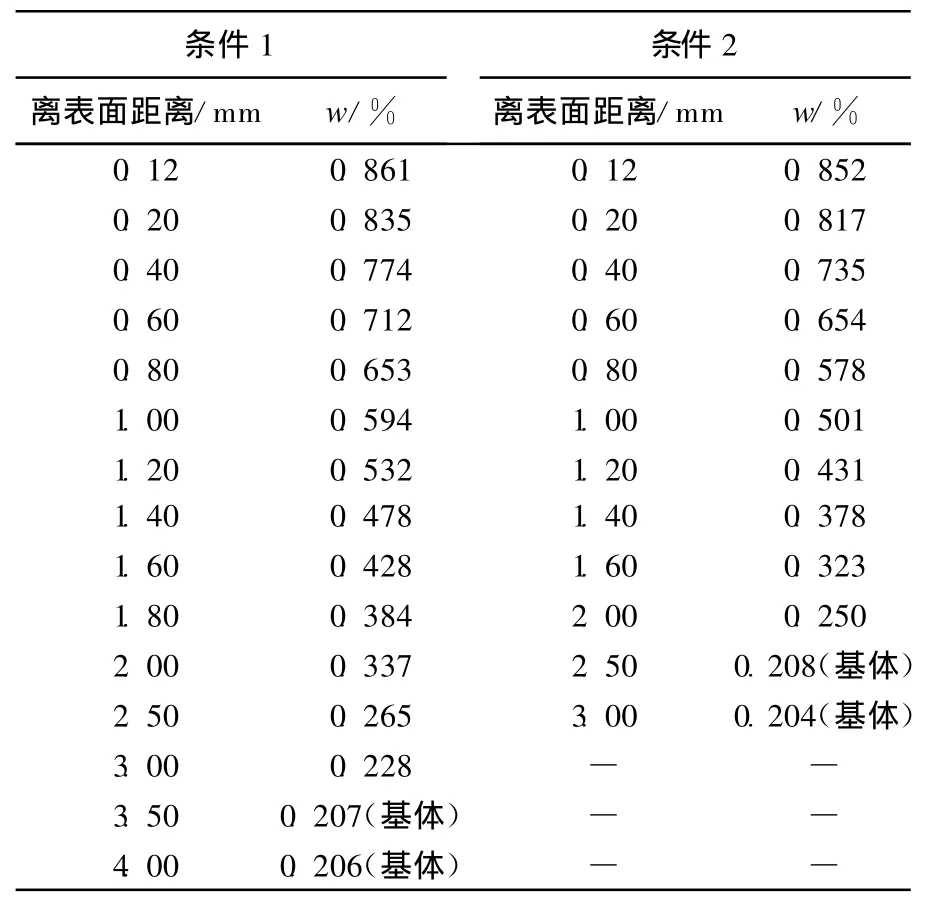
表3 渗碳件试验数据

从表1和表 3知,计算值与试验数据吻合较好。

3 结 论

运用CSYHXT对两段渗碳工艺进行优化设计,能缩短渗碳周期约15%～20%。渗碳质量控制的关键是表面碳含量和硬化层深度的设计,带有水平台阶的“凸形”碳含量分布曲线是其理想状况的表现形式。渗层碳含量分布控制的关键在于选择合理的强渗时间与扩散时间的比例,但这种关系并不固定,运用本系统可针对不同的渗碳条件,找出其t1/t2的最佳比值。采用两段渗碳时,高碳势强渗期不宜过长,以避免碳化物级别过高。运用模块化的形式进行软件系统开发,有利于多种语言的混合编程,更为系统的扩展和维护提供了方便。

[1] 李 云.两段法渗碳扩散方程的解析解[J].金属热处理学报,2000,21(1):50-51.

[2] 杨桂生.碳势设定与调节及其对深层渗碳的影响[J].国外金属热处理,2002,23(6):31-32.

[3] 凌国平,马智勇.气体渗碳动力学的研究[J].金属热处理,2000,(2):36-38.

[4] 闫 锦,王振清,张建华,等.计算机辅助确定渗碳工艺参数[J].新技术新工艺,1996,(1):3-4.

[5] 武大权.渗碳层碳浓度分布的推导及应用[J].金属热处理,1995,(9):29-30.

[6] 齐从谦.C程序设计教程[M].北京:机械工业出版社,2007:50-58.

[7] 孙家启.C语言程序设计[M].合肥:中国科学技术大学出版社,2005:132-143.

[8] 牛允鹏.数据库及其应用[M].南京:南京大学出版社,1994:87-90.