平衡损失下带约束的回归系数的线性容许估计

曹明响, 孔繁超

(1.合肥师范学院数学系,安徽 合肥 230061;2.安徽大学数学与计算科学学院,安徽合肥 230039)

设有线性模型为:

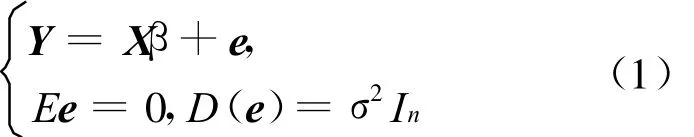
其中,X为n×p阶列满秩阵;β∈Rp和σ2＞0为未知参数;D(e)表示随机变量e的方差。回归系数 β的最小二乘估计ˆβ ≜(X′X)-1X′Y 定义为使

达到最小的d值,最小值是建立后模型的一种拟合优度。对于ˆβ的统计性质,人们主要是从估计的精度来考虑它的优良性。从统计判决理论角度看,就是在损失函数

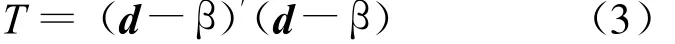
下,选取使风险达到最小的估计。作为(2)式和(3)式2种标准的综合,文献[1]提出了一个新的称为平衡损失函数的标准,即

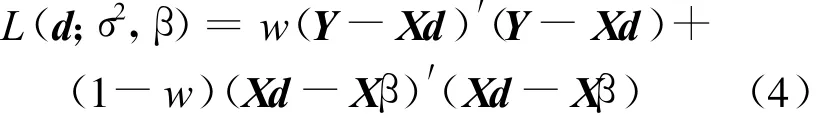
其中,w∈[0,1]已知。(4)式既考虑了估计的精度,又考虑了模型拟合的优良程度,所以它是一个更全面和合理的标准。

采用(4)式研究一些特定估计的风险函数已有一些结果,如文献[2～4]等。文献[5]对(1)式在(4)式下,得到了回归系数的线性容许估计的充要条件。然而在实际问题中,回归系数通常带有某些约束;文献[6]研究了(5)式在(4)式下,回归系数的线性容许估计的充要条件,但所给的结论有误。

本文给出了正确的结论,并利用矩阵的向量化方法[7]研究了带线性约束的多元线性模型在矩阵形式的平衡损失函数下,回归系数的线性估计的可容许性[8]。

本文采用如下记号:对任意矩阵A,A′、A-1、A-、rk A,tr A和 Μ(A)分别表示矩阵A的转置、逆矩阵、广义逆矩阵、秩、迹和A的列向量组成的线性空间。vec(A)表示将A的各列拉直所成的向量,称为A的向量化。A⊗B表示矩阵A和B的Kronecker乘积,A≥B表示A-B为非负定阵。

对于模型

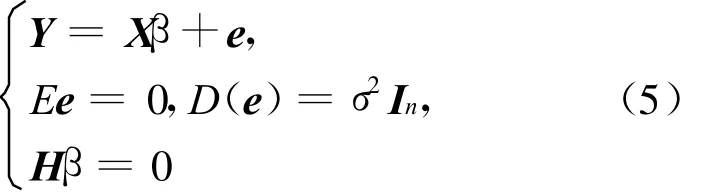
其中,H为 l×p阶矩阵,其他记号与(1)式中相同。

取线性估计类:

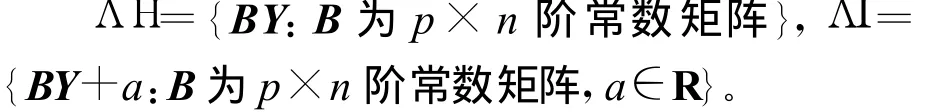
下面给出文献[6]中的正确结论作为引理,它们的证明见文献[6]。

引理1 在(4)式和(5)式下,BY是β在 Λ Η中容许估计的充要条件是:

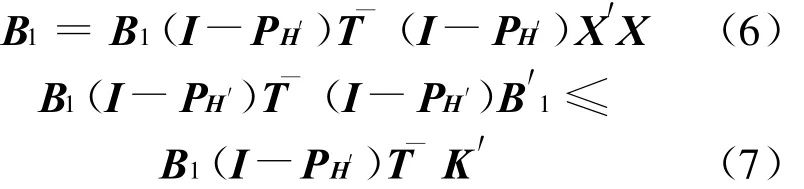
引理2 在(4)式和(5)式下,BY+a是β的在Λ Ι中容许估计的充要条件是(6)、(7)式和 a∈Μ((BX-Ip)(I-PH′))同时成立 ,其中 :

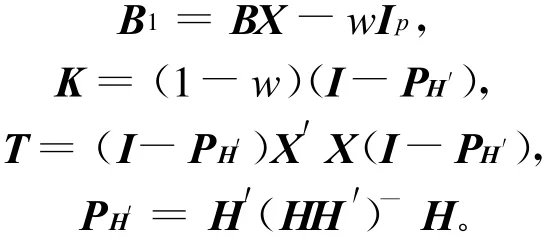
1 预备知识

考虑带线性约束的多元线性模型为:

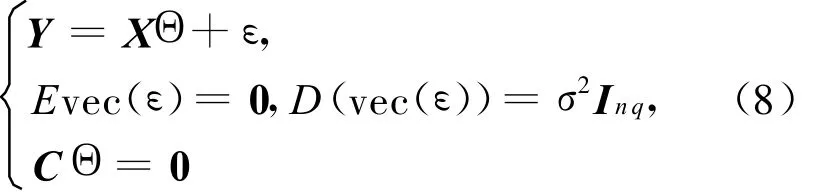
其中,Y、ε是n×q阶随机阵;X为n×p阶列满秩阵;p×q阶矩阵 Θ和σ2＞0均为未知参数;C为k×p阶矩阵。取线性估计类阶常数阵},和 Dp×q均为常数阵}。对于(8)式,(4)式不再适用。这里给出矩阵形式的平衡损失函数为:

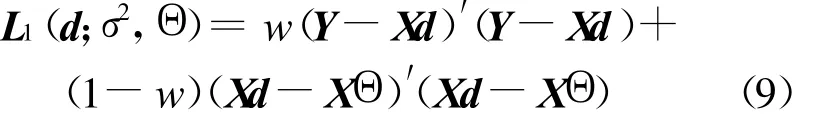
且相应的风险函数为:

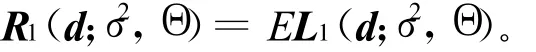
由于比较矩阵大小的标准有多种,这里给出其中一种最优标准。

定义1 设G1(Y),G2(Y)都是参数 Θ的估计,若对任意满足C Θ=0的 Θ有:

利用矩阵的向量化运算,将(8)式转化为一元线性模型为:

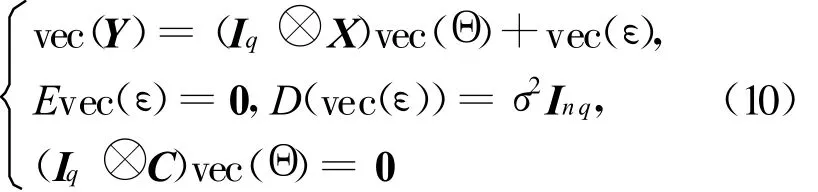
引理3

证明 仅证(1),(2)的证明类似。由于

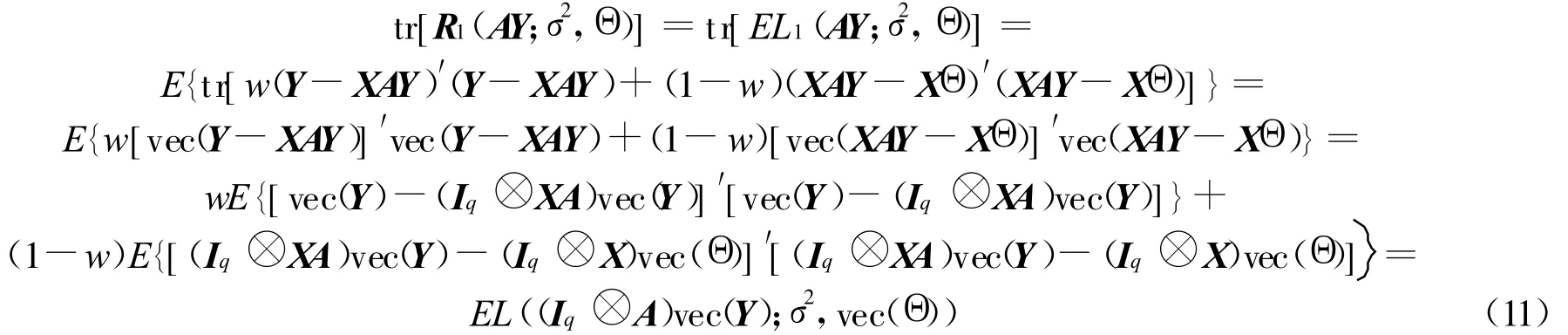
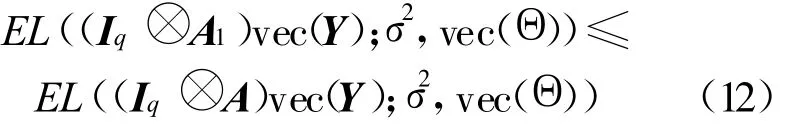
《全唐诗》中唐代明确涉及隋堤柳意象的诗歌有80余首,但从诗歌的创作时间上来看,初盛中晚各时段显得十分不均衡。早在贞观时期,唐太宗《春池柳》即有“年柳变池台,隋堤曲直回”[注]彭定求等:《全唐诗》(增订本)卷1,北京:中华书局,1999年,第15页。 的诗句,但这还不能算是明确的隋堤柳诗歌意象。整个初盛唐近140年的时间里,除了个别诗人,隋堤柳并未纳入唐代诗人的抒情视野。直到安史之乱后,相关作品才开始涌现。

由(11)式可得:

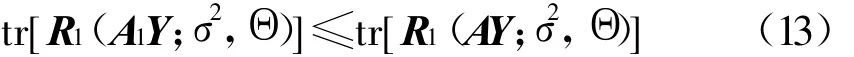
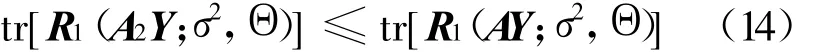
再由(11)式可得:

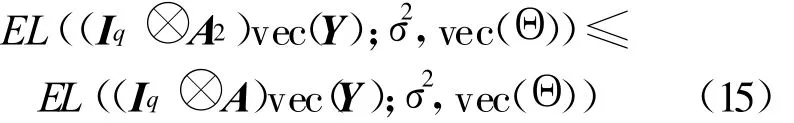
从而引理3得证。

证明 记 PX=X(X′X)-1X′,若 (Iq⊗A)vec(Y)∈Λ2Η,则易得:

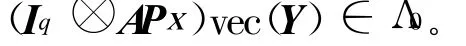
由于

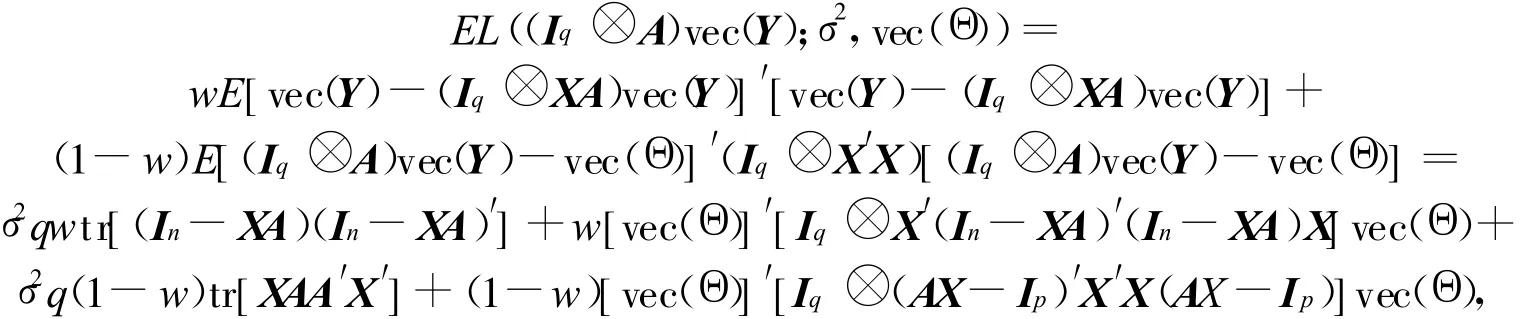
从而可得它们的风险之差为:

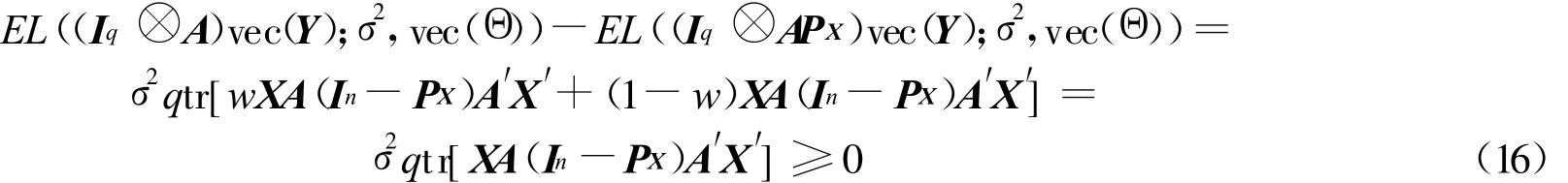
且(16)式对所有σ2＞0和满足的 Θ都成立,等号恒成立当且仅当A=APX。

2 主要结果

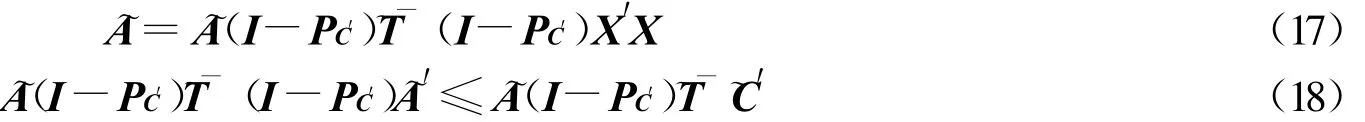
由引理1可得:

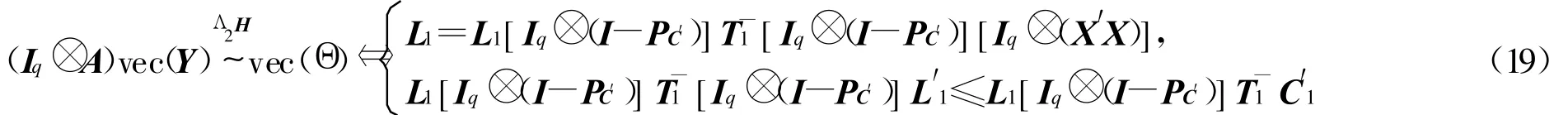
其中

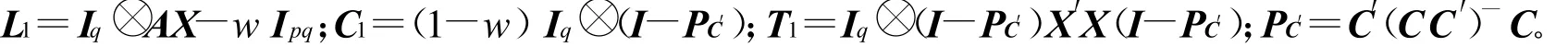
从而由矩阵的向量化运算可得:

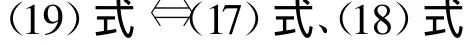
定理1得证。

由引理3的(2)和引理2,使用类似定理1中的证明方法,可得下面的定理2。

[1] Zellner A.Bayesian and non-Bayesian estimation using balanced loss function[M]//Gupta S S,Berger J O.Statistical Decision Theory and Related T opics.Berlin:Springer-Verlag,1994:377-390.

[2] Wan A T.Risk comparison of inequality constrained least squares and other related estimators under balanced loss[J].Economics Letters,1994,15:203-210.

[3] Rodrignes J,Zellner A.Weighted balanced loss function and estimation of the mean time to failure[J].Communications in Statistics:Theory and M ethods,1994,27:3609-3616.

[4] Ohtani K.The exact risk of a weighted averge estimator of the OLS and Stein-rule estimators in regression under balanced loss[J].Statistics and Descisions,1998,16:35-45.

[5] 徐兴忠,吴启光.平衡损失下回归系数的线性容许估计[J].数学物理学报,2000,20(4):468-473.

[6] 王 剑,屈思敏.平衡损失下回归系数线性估计的容许性[J].太原师范学院学报,2006,5(3):1-3.

[7] 王松桂,史建红,吴密霞,等.线性模型引论[M].北京:科学出版社,2004:75-154.

[8] 陈希孺,陈桂景,吴启光,等.参数的估计理论[M].北京:科学出版社,1985:34-98.