函数幂型几何平均亚式期权定价研究

孙江洁

(安徽医科大学临床医学院,安徽合肥 230601)

0 引 言

幂型期权和亚式期权是2种新型期权,其中,亚式期权是一种依赖于期权在到期日 T时的受益的奇异期权,它不仅取决于资产到期日的价格,还与整个期权有效期[0,T]内,某段时间标的资产所经历的价格平均值有关。这里的平均值可以取算数平均值,也可以取几何平均值。而幂型期权也是一种新型期权,它改变了资产的定价结构,大大提高了所定价格对时间的敏感度。幂型亚式期权又是两者的统一,为了更好地规避风险,研究幂型亚式期权具有很大的实践意义。

文献[1]讨论了几何平均亚式期权的定价问题,文献[2]给出了欧式幂型期权的定价公式,文献[3]讨论了常系数幂型亚式期权的定价问题,文献[4]对函数系数的几何亚式期权进行了研究。本文利用鞅测度变换的方法,得到了连续时间的函数幂型几何平均亚式看涨期权的定价公式。本文所涉及的随机积分理论可参考文献[5,6]。

1 资产模型及主要结果

假定市场是完全,无套利的,只有风险资产和无风险资产,其价值过程:{St:t≥0}和{B(t):t≥0}且满足如下微分方程:

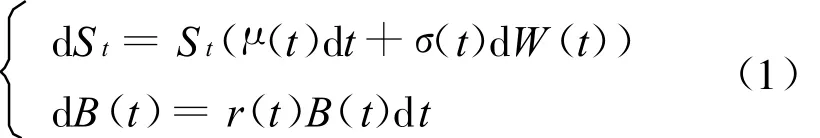
其中,{W(t)}t≥0是带σ-代数流的概率空间(Ω,F,{Ft}t≥0,P)上的标准布朗运动 ;r(t),μ(t),σ(t)均是依赖于时间的确定性函数,且是[t,T]上的L-可测函数。

定理 在模型(1)下,连续时间的函数幂型几何平均亚式看涨期权在t时刻的价值为:

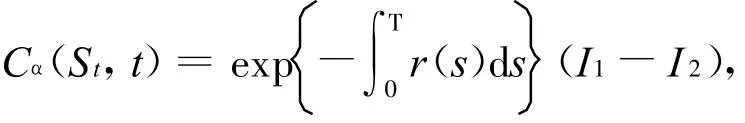
其中

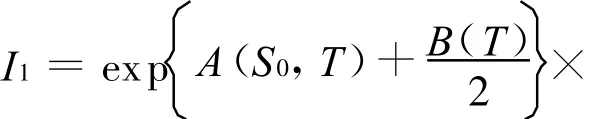
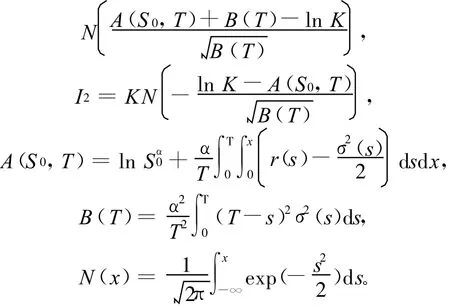
推论 特别地,当 r(t)=r,σ(t)=σ,且 r,σ均为常数时,有:

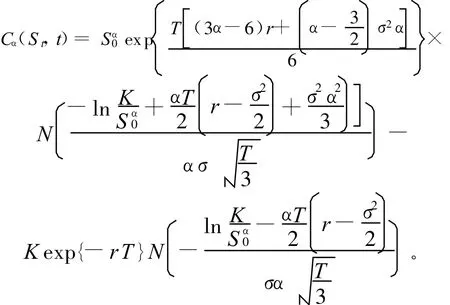
证明 只需将r(t)=r,σ(t)=σ代入定理,即可得证。

2 若干引理

引理1(Girsanov定理[7,8]) 取W(t)(t≤s≤T)为带 σ-代数流的概率空间(Ω,F,{Fs}s≥t,P)标准布朗运动,θ(s)(t≤s≤T)是一个适应于{Fs}s≥t的随机过程 ,对 t≤s≤T,定义:

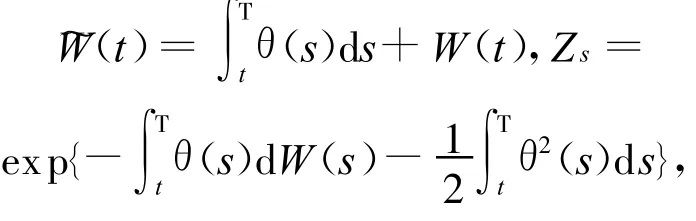
引理2[2,9]幂型期权在到期日计算价值时,用S(T)α≜(α为实现确定的实数)与执行价格K做比较,即幂型期权的支付形式是:max{-K,0},且其对应的期权支付形式为:max{STK,0}。

引理3 连续时间的函数幂型几何平均亚式看涨期权的支付形式可写为:

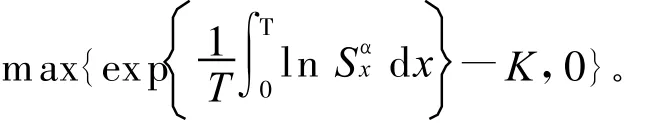
证明 由引理2及连续时间的几何平均亚式

看涨期权的支付形式为:

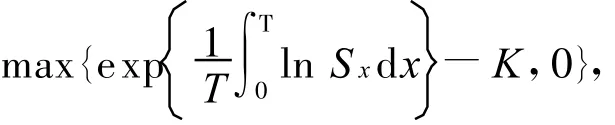
可类推得到引理3成立。

3 定理的证明

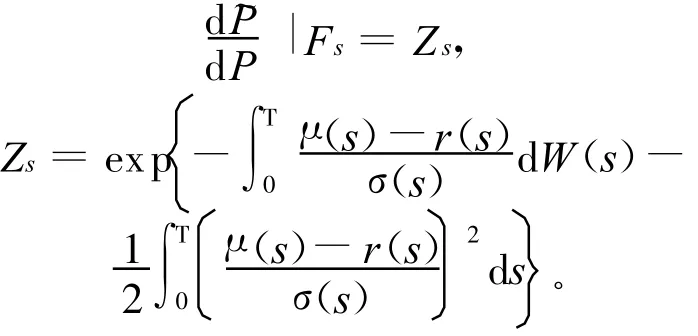
容易算得:

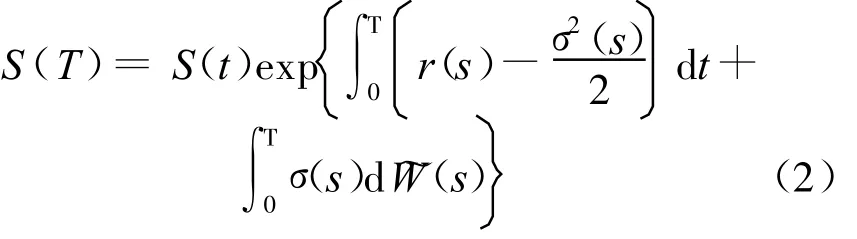
由引理3可知,在模型(1)下,连续时间的函数幂型几何平均亚式看涨期权在 t时刻的价值为:

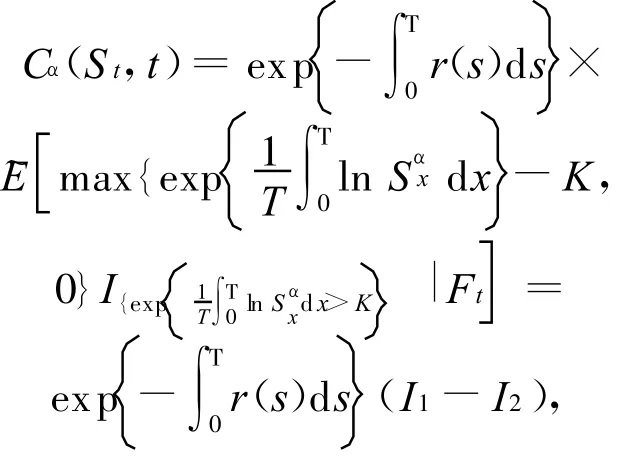
其中

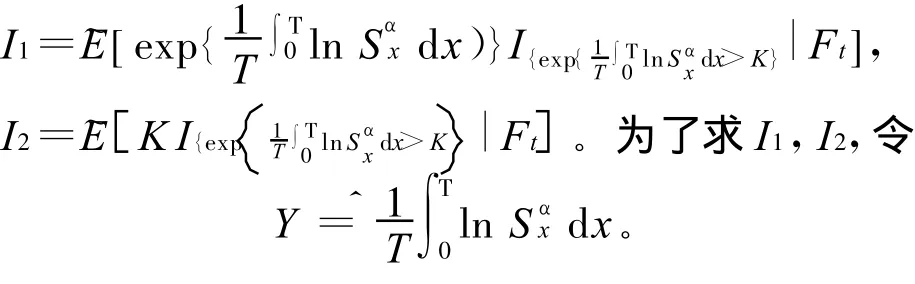
则有:

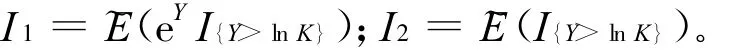
先求 I1,结合(2)式,可得到:

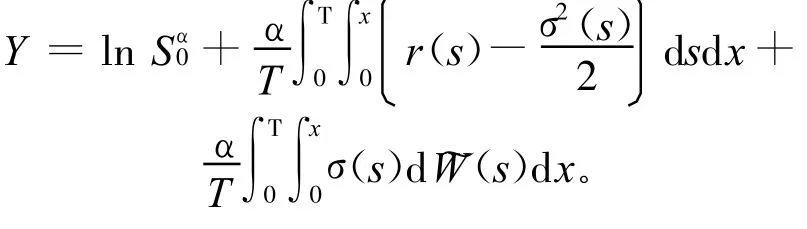
由随机积分的相关知识可知:

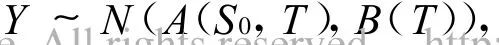
故由概率统计的相关知识有:

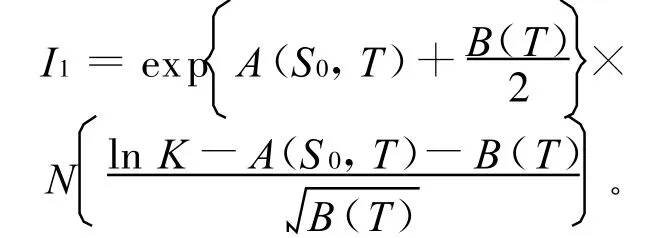
利用正态分布的密度函数容易算出:

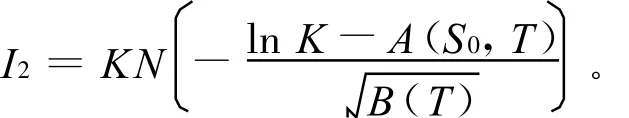
证毕。

4 结束语

本文利用鞅测度变换的方法,得到了连续时间的函数幂型几何平均亚式看涨期权的定价公式显式解,在本文的定理中,当r(t)=r,σ(t)=σ,且r,σ均为常数时,即可得到文献[4]的结论,在本文的推论中,令 α=1,即可得到文献[1]的结论。

[1] 章 珂,周文彪,沈荣芳.几何平均亚式期权的定价方法[J].同济大学学报(自然科学版),2001,29(8):924-927.

[2] 陈万义.幂型支付的欧式期权定价公式[J].数学的实践与认识,2005,(6):52-55.

[3] 王亚军,张 艳,范胜尹.幂型亚式期权的定价问题[J].徐州建筑职业技术学院学报,2006,6(2):39-41.

[4] 罗庆红,杨向群.几何亚式期权的定价研究[J].湖南文理学院学报,2007,19(1):5-8.

[5] Ameur H B,Breton M,Karoui L,et al.A dynamic programming approach for pricing options embedded in bonds[J].Journal of Economic Dynamics&Control,2007,31:2212-2233.

[6] Shreve S E.Stochastic calculus for finance:continuoustime models[M].New York:Springer-Verlag,2004:198-210.

[7] M usiela M,Rutkowski M.Martingale methods in financial modelling[M].New York:Springer-Verlag, 2003:110-116.

[8] 孙江洁,杜雪樵.Vasicek利率模型下的欧式期权买权定价[J].合肥工业大学学报(自然科学版),2009,32(3):442-445.

[8] 茅 宁.期权分析理论与应用[M].南京:南京大学出版社,2000:3-970.