轴向变速黏弹性梁非线性动力学行为数值研究

唐 震, 张学勇, 黄 凯, 李 平, 刘 东

(安徽建筑工业学院数理系,安徽合肥 230601)

0 引 言

动力传送带、带锯、空中缆车索道及高楼升降机缆绳等多种工程系统元件,计及抗弯刚度时均可模型化为轴向运动梁。因此,轴向运动梁的研究有广泛的应用前景。

同时,轴向运动梁的控制方程中含有时间和空间混合偏导数项,是典型的陀螺连续系统,相关研究也有重要的理论意义。

随着轴向运动弹性梁非线性振动研究的深入[1,2],对轴向运动黏弹性梁的非线性振动也开始研究。

对于轴向运动梁非线性动力学行为的研究往往是采用 Galerkin截断,Kapitaniak还基于Galerkin截断用数值方法研究了轴向运动黏弹性梁轴向力变化导致非线性参数振动的分岔和混沌[3]。文献[4,5]分别基于2项和4项Galerkin截断用数值方法研究轴向运动黏弹性梁轴向力变化导致非线性参数振动的分岔和混沌,但是尚无直接的证据证明低阶Galerkin截断的合理性[6],而采用直接数值方法研究轴向运动系统非线性动力学行为的报道很少。

黏弹性的引入,提供了工程系统中阻尼因素建模的一种可能途径。本文研究Kelvin黏弹性本构关系非线性梁在速度有周期脉动时的运动特性,采用有限差分法对运动微分方程直接数值解,研究高速运动状态下,速度的脉动对梁运动特性的影响。研究结果发现,系统在某些参数情况下平衡位置会失去稳定性,而出现周期运动或者混沌运动。

1 控制方程

考虑Kelvin微分黏弹性本构关系,利用牛顿第二定律得到变速轴向运动梁横向振动的控制方程[7],无量纲化后得到非线性偏微分方程为:

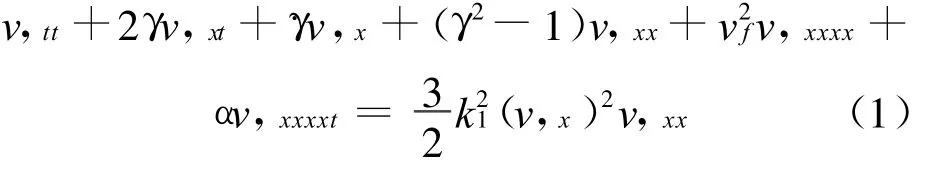
其中,梁上点的横向运动位移v为空间轴向坐标x及时间t的函数;γ表示梁的轴向速度;vf表示刚性系数;α表示黏性系数;k1表示非线性系数(其中,逗号表示对其后面的变量求偏导数,符号上方的点表示对时间t求导数)。

2 数值方法

有限差分法是求解微分方程的有效数值方法,它将偏微分方程的求解转化为代数方程的求解,即函数在给定点处的导数值可以近似地用邻近节点函数值表示。

引入等间距网格L×T,以及时间步长τ和空间步长h,即

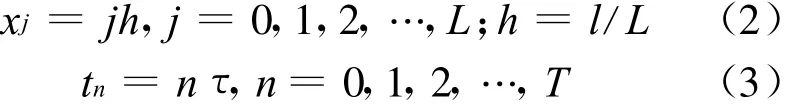
考虑梁的两端由光滑套筒简支的边界条件为:

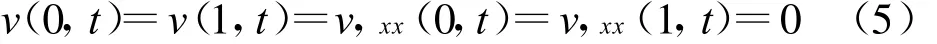
在本文的研究中,将使用以下初始条件:

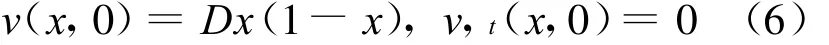
其中,D为初始振幅,本文取D=0.001。

在给定系统各参数的值之后,可数值求解代数方程组,实现对(1)式的数值解。

3 数值算例

这里假设无量纲化的梁轴向运动速度在一个恒定的平均速度γ0附近有幅值为γ1,频率为ω的周期性简谐扰动,即

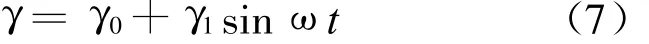
考虑运动梁的参数设置为刚度vf=0.8,非线性系数k1=2 000,α=0.001,平均速度 γ0=3,扰动速度频率 ω=3.5。其计算时间步长为0.000 001,空间步长为0.001。

图1所示给出了2倍周期运动的梁中点随时间变化的相平面、Poincar映射图、梁中点时程以及时程的频谱分析,其中γ1=0.40。

从图1可以清楚地识别此时系统处于倍周期运动状态。

图1 2倍周期运动

图2所示给出了混沌运动的梁中点随时间变化的相平面、Poincar映射图、梁中点时程以及时程的频谱分析,其中γ1=0.47。从图2可以判定系统此时处于混沌运动状态。

图3所示给出了非线性参数振动稳态周期运动和混沌运动随时间变化的最大 Lyapunov指数,其中图3a中扰动速度的幅值 γ1=0.40;图3b中扰动速度的幅值γ1=0.47。从图3中可以看出,系统振动时周期运动的最大Lyapunov指数会随时间而趋于零,而混沌运动的最大Lyapunov指数会趋于一个正值。

根据时间序列的最大Lyapunov指数,同样可以判定系统是处于周期运动状态还是混沌运动状态。

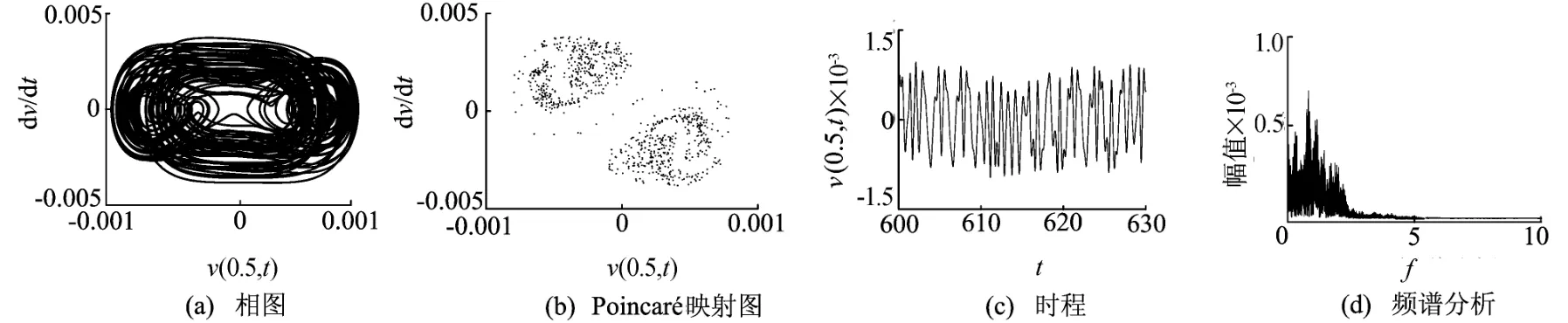
图2 混沌运动

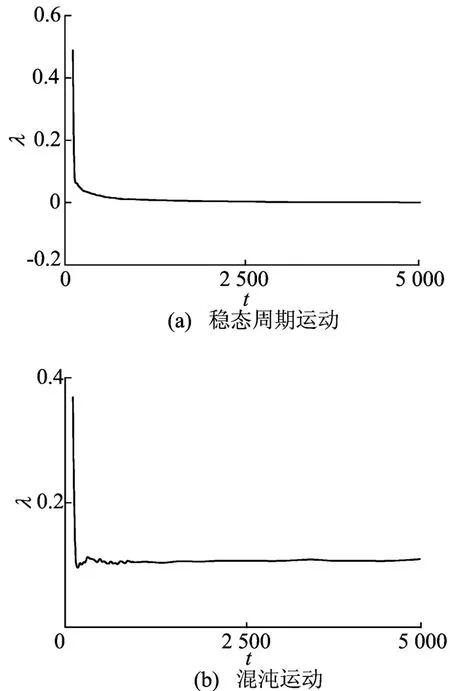
图3 随时间变化的最大Lyapunov指数

4 结束语

本文根据Kelvin黏弹性本构关系的轴向变速运动梁的动力学方程,利用有限差分法对系统运动的偏微分方程数值解,研究了非线性黏弹性脉动运动梁的振动形式,通过时间序列分析,分别用相图、Poincar映射图、时间历程、频谱分析和最大Lyapunov指数方法,识别了系统的周期运动及混沌运动形态。

[1] 冯志华,胡海岩.基础直线运动柔性梁的非线性动力学[J].振动工程学报,2004,17(3):126-131.

[2] Chen Shuhui,Huang Jianliang,Sze K Y.M ulti-dimensional Lindstedt-Poincaré method for nonlinear vibration of axially moving beams[J].Journal of Sound and Vibration,2007,306(2):1-11.

[3] M arynowski K.Non-linear vibrations of an axially moving viscoelastic web with time-dependent tension[J].Chaos,Solitons and Fractals,2004,21(2):481-490.

[4] Yang Xiaodong,Chen Liqun.Bifurcation and chaos of an axially accelerating viscoelastic beam[J].Chaos,Solitons and Fractals,2005,23(1):249-258.

[5] Chen Liqun,Yang Xiaodong.T ransverse nonlinear dy namics of axially accelerating viscoelastic beams based on 4-term Galerkin truncation[J].Chaos,Solitons and Fractals,2006,27(3):748-757.

[6] 陈立群,程昌钧.非线性黏弹性梁的动力学行为[J].应用数学和力学,2000,21(9):897-902.

[7] 刘延柱.刚体动力学理论与应用[M].上海:上海交通大学出版社,2006:259-299.

[8] Boresi A P,Ken P C,Sunil S.Approximate solution methods in engineering mechanics[M].New York:Wiley,2003:42-47.