阻尼对地铁引起地面振动计算的影响

李守继, 楼梦麟

(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;2.同济大学 土木工程防灾国家重点实验室,上海 200092)

0 引 言

近年来,随着经济的快速发展,一方面,地铁在城市交通中得到愈来愈广泛的应用[1];另一方面,由于生活水平的提高,人们对环境要求愈来愈高。因此,地铁对环境的影响越来越大。地铁运行引起的振动虽不致造成建筑物结构破坏,但可能造成装饰物开裂脱落;较大振动会影响人们的生理和生活,影响精密仪器等对振动敏感设备的正常工作[2]。因此,地铁振动对环境的影响引起人们越来越广泛的关注,受到各国研究人员的高度重视[3]。

同济大学土木工程防灾国家重点实验室振动与地面运动观测室曾多次利用ALTUS-K2测振仪,在上海多条地铁周边场地进行了现场振动测量,获得地铁引起地面振动的加速度时程记录。结果表明,地铁引起地基土振动的频率成分非常复杂,主要为中高频振动[4]。

目前,人们在进行结构动力计算分析时,阻尼多采用Rayleigh比例阻尼模型[5],该模型采用2个控制频率来确定阻尼比例系数。一般来说,在土层动力反应的时域计算中,多采用土层的低阶自振频率,特别是第1阶自振频率来确定 Rayleigh比例阻尼模型中的2个比例系数。这一方法应用于较浅土层地震反应的计算是可行的,已有研究[6]表明,在深覆盖土层地震反应分析中采用这一方法时,存在严重低估土层地震反应的可能性。这是因为土层地震反应计算中输入地震波的主要成分的迫振频率远高于土层的基频,以土层基频来确定的Rayleigh比例阻尼矩阵将大幅提高高阶振型的阻尼比,抑制高阶振型对土层地震反应的贡献。类似地,在计算由地铁运行引起的土层振动分析中也同样存在激振频率远高于土层或地下结构低阶自振频率的情况,如何合理确定阻尼矩阵是应重视的问题。本文试图应用Caughey阻尼模型[7]与 Rayleigh阻尼模型来讨论阻尼模型在地铁引起土层振动分析中的影响。

1 Caughey阻尼模型

1.1 阻尼比与频率的关系

人们进行结构动力计算分析时,之所以采用(1)式所示的 Rayleigh阻尼矩阵[7],是为了满足正交条件,从而使求解动力方程时能够解耦。

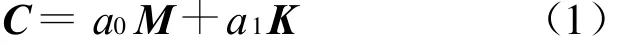
式中,系数a0和a1由2个控制频率确定。

而由结构的质量矩阵和刚度矩阵可组合成无数个满足正交条件的矩阵。可以证明,自由振动振型关于k(m-1k)b矩阵和m(m-1k)b矩阵均正交,因此正交的阻尼矩阵(用矩阵形式表示)可写成如下形式:

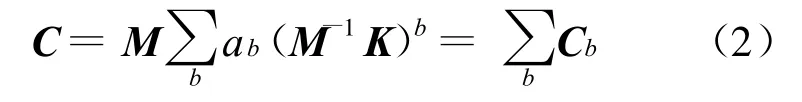
式中,ab为任意系数;当 b取任意项,即形成Caughey阻尼公式。当b仅取0和1两项时,即得(1)式所示的Rayleigh阻尼公式。

又第n振型的广义阻尼为:

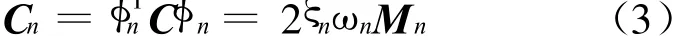
当阻尼由(2)式给出时,由(3)式可得:

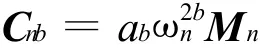
则

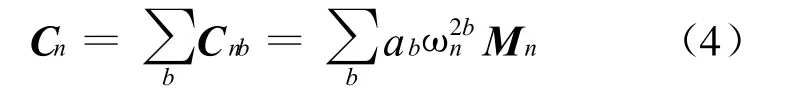
比较(3)式和(4)式,有:

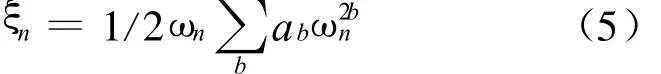
取b为0及其附近的共i个整数,并给定相应的i个阻尼比ξi和相应的ωi,则利用(5)式解得对应的i个ab值。利用解得的ab值,可建立以频率 ω为自变量,ξ为因变量的函数,即

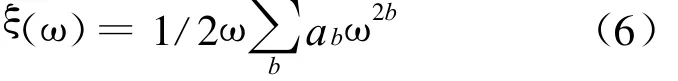
1.2 阻尼比随频率变化特征

为讨论2种阻尼模型对不同振型阻尼比的影响,假定振动体系各阶振型的实际阻尼比是相同的,所考察的振动体系的振型阻尼比分别为0.01、0.03和 0.05三种情况。

图1所示绘出采用 Rayleigh阻尼模型(即i=2,b分别取0和1)时,由(6)式描述的振型阻尼比随频率变化的曲线,其中对应控制频率分别取 ω1=2π◦1,ω2=2π◦80。采用 Caughey阻尼模型时,取 i=7,b分别为 -1、0、1、2、3、4 和 5,对应控制频率分别取 ω1=2π◦1,ω2=2π◦2,ω3=2π◦10,ω4=2π◦30,ω5=2π◦50,ω6=2π◦70 和ω7=2π◦80,则由(6)式描述的振型阻尼比随频率变化的曲线如图2所示。

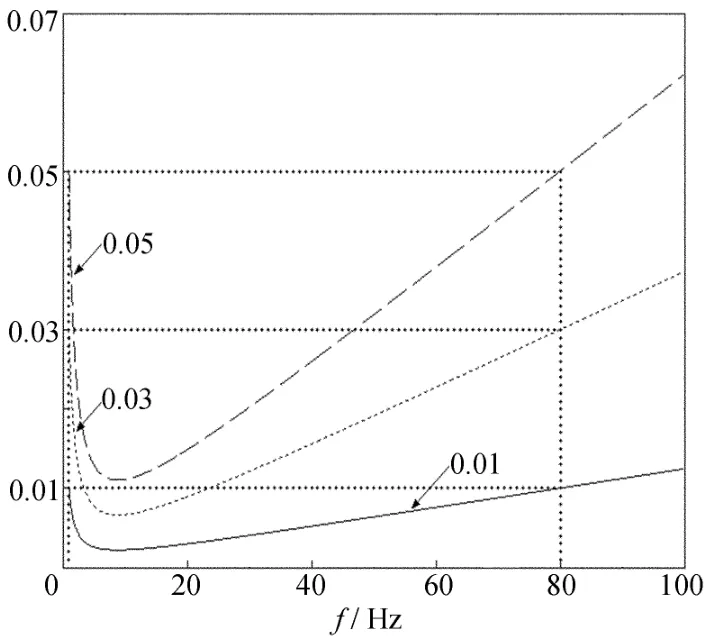
图1 由2个基本频率决定的阻尼比-频率曲线

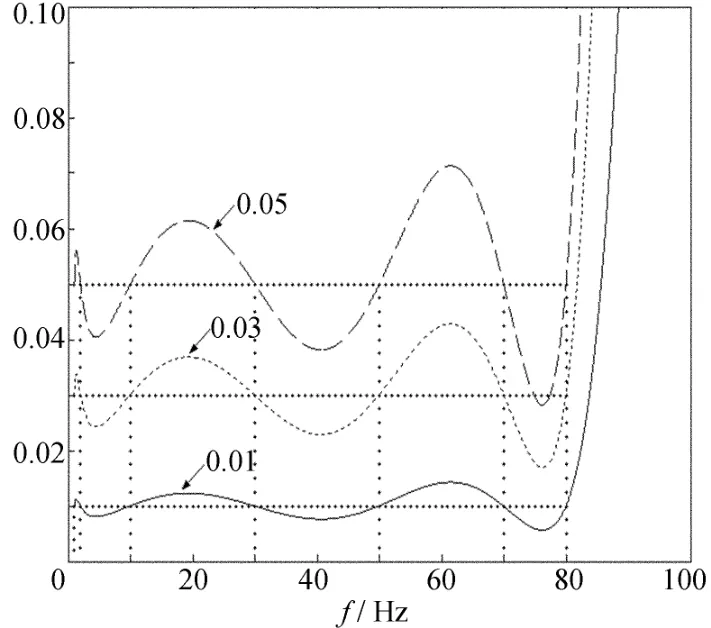
图2 由7个基本频率决定的阻尼比-频率曲线

1.3 控制频率的确定

由上述曲线可见,阻尼比-频率曲线波动大小与控制频率个数、两相邻控制频率之间的间距大小和控制起始频率大小等因素有关。控制频率的个数i太少,如取2个控制频率,即Rayleigh比例阻尼时,控制频率之间部分的计算阻尼比小于实际的振型阻尼比,如图1所示。显然,当结构以控制频率之间的频率振动时,振动反应计算值比实际反应值要小。

一般来说,两相邻控制频率之间的间距越大,其间阻尼比误差越大。但当控制频率的个数i太大时,又会出现与实际不符的阻尼比小于零的情况。

综上计算分析,对于0～80 Hz频率范围的振动,按图2所示选取的7个控制频率来确定振动体系的阻尼矩阵比较合适。由此建立的Caughey阻尼模型为:

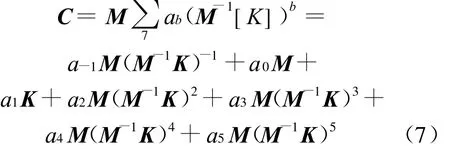
式中,系数ai由 7个控制频率 f-1=1 Hz、f0=2 Hz、f1=10 Hz、f2=30 Hz、f3=50 Hz、f4=70 Hz和f5=80 Hz按(8)式得到。

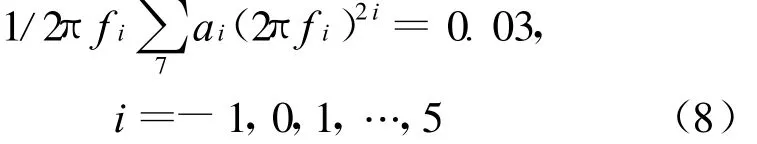
2 算 例

下面通过工程实例来验证。利用上海典型土层参数,建立包括地铁隧道在内的分层土层有限元计算模型。采用Caughey阻尼和Rayleigh阻尼2种方法,计算比较在地铁引起复杂频率振动的激励下,土层的振动响应。

2.1 土层计算参数、激励和计算方法

2.1.1 计算参数

考虑比较结果的相对性及便于计算,将上海市典型土层计算参数[8]按厚度加权进行适当归并,并且取深度为150 m得表1所列。表中平均剪切模量是根据弹性波传播理论指出的剪切波速vs、介质剪切模量G和介质弹性模量E之间存在下列关系[9],计算得到:

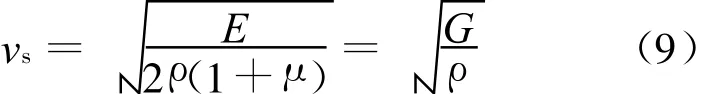
式中,ρ为介质密度;μ为泊松比。

2.1.2 激 励

输入激励为对地铁引起的轨道实测竖向振动加速度,时程取时间步长为0.005 s而得到,时程曲线如图3所示,图4所示为其Fourier幅值谱。

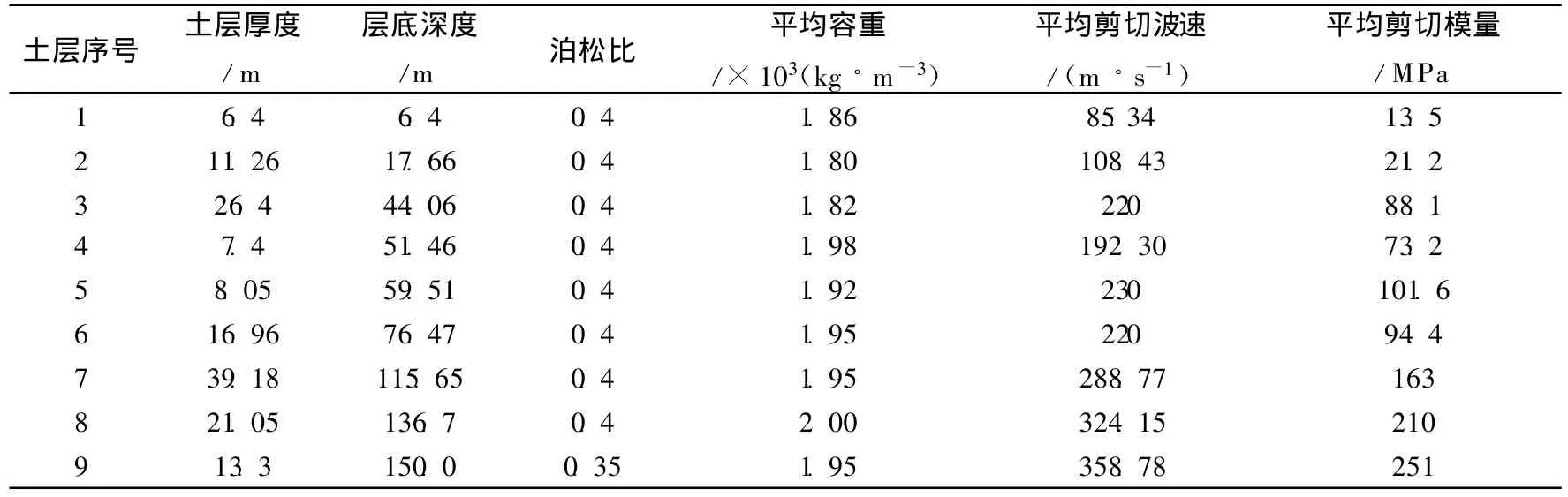
表1 土层计算参数

2.1.3 计算方法

由建立的Caughey阻尼模型和土层有限元的质量矩阵、刚度矩阵[10],利用Newmark逐步积分法计算土层有限元各节点的位移、速度和加速度响应。

2.2 计算模型

根据施工工程所在地的上海地铁一号线某处隧道横截面尺寸[11](如图5所示)和前述土层计算参数等,建立土层二维有限元计算模型,如图6所示。

考虑对称性、计算条件并忽略另一方向行驶列车隧道的影响,计算模型为以竖向对称轴的整体模型的一半,横向尺寸取300 m,竖向尺寸取150 m,满足模型最小范围应取3H ×H(H为基岩深度)的要求[12]。模型底部为固定约束;对称轴,即图6所示模型右边界,仅水平方向约束;左边界无约束。

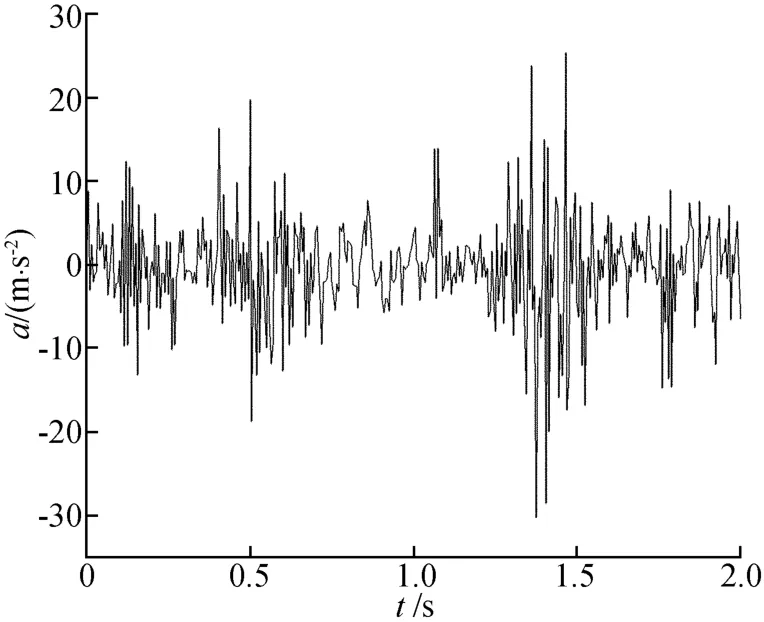
图3 激励加速度时程曲线

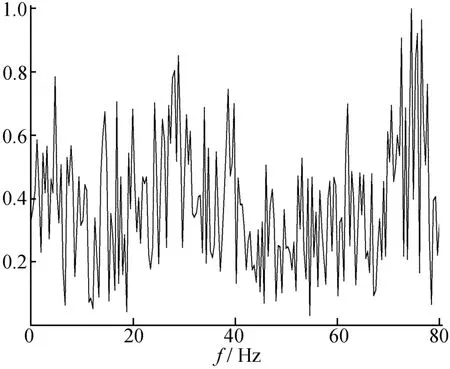
图4 激励加速度Fourier幅值谱曲线

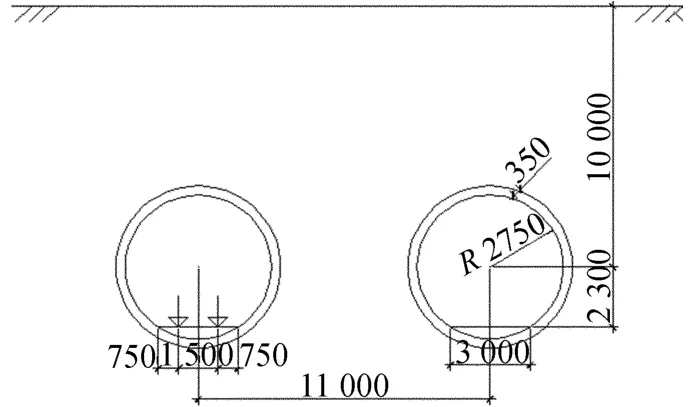
图5 地铁隧道横截面图

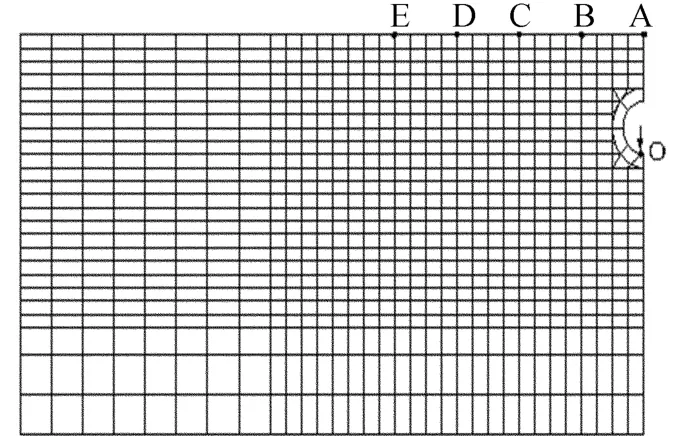
图6 土层有限元计算模型示意图

2.3 计算结果及分析

表2列出计算土层前10阶自振频率;表3列出图6所示土层表面A点、B点(距A点30 m)、C点(距A 点60 m)、D点(距A 点90 m)和 E点(距A点120 m),阻尼分别按(7)式Caughey阻尼和Rayleigh阻尼算得的振动响应峰值加速度。

表2 计算土层自振频率

表3 计算节点峰值加速度 m/s2

图7和图8分别绘出图6所示土层表面A点和E点,按Caughey阻尼(图中记为柯西阻尼法)和Rayleigh阻尼(图中记为瑞雷阻尼法)算得的竖向振动响应加速度时程曲线。

计算分析表明,按Caughey阻尼方法计算得到的地面位移、速度和加速度响应均要比按Rayleigh阻尼方法算得的结果大;按2种阻尼方法算得的A点、B点、C点、D点和E点竖向振动位移最大误差分别为 3%、9%、18%、31%和38%;速度最大误差分别为 11%、26%、45%、64%和52%;加速度最大误差分别为34%、46%、59%、67%和72%;相同情况下,加速度误差比位移和速度误差均要大。

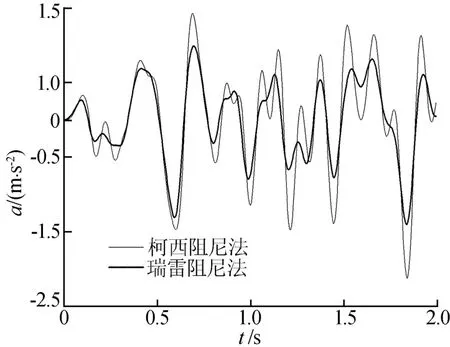
图7 A点竖向振动响应加速度时程曲线

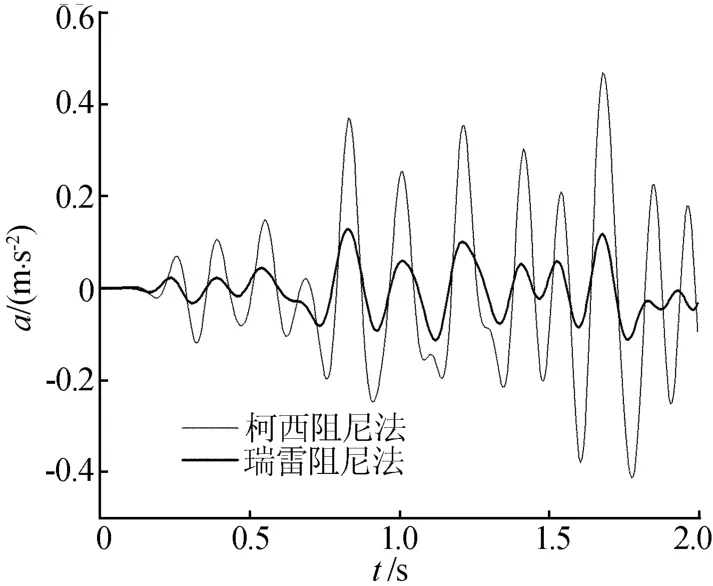
图8 E点竖向振动响应加速度时程曲线

3 结 论

本文利用2种阻尼模型,计算分析了地铁引起地面振动的位移、速度和加速度响应。计算结果表明:

(1)对于频率分布较广的中高频振动,需合理选择控制频率来确定阻尼比,从而使振动在整个频率范围内的阻尼比与事先确定的控制阻尼比之差满足要求。

(2)当土体受到频率分布较广的中高频振动激励,计算土体响应时,阻尼采用传统的Rayleigh阻尼,将会使计算结果偏小。

(3)目前,计算地铁引起土体的振动响应,多采用Rayleigh阻尼。本文首次尝试利用Caughey阻尼计算地铁引起土体的振动响应。由于地铁振动频率分布非常广,土体特性复杂,如何选择更符合实际的阻尼模型还有待进一步深入研究。

[1] 钱七虎,戎晓力.中国地下工程安全风险管理的现状、问题及相关建议[J].岩石力学与工程学报,2008,27(4):649-655.

[2] Hung H H,Yang Y B.A review of researches on ground-borne vibrations with emphasis on those induced by trains[J].Proceeding of the National Science Council,ROC(A),2001,25(1):1-16.

[3] BalendraT,Chua H,Lo K W,et al.Steady-state vibration of subway-soil-building system[J].Journal of Engineering Mechanics,1989,115(1):145-162.

[4] 楼梦麟,李守继,丁洁民,等.基于多点输入的地铁引起房屋振动评价研究[J].振动与冲击,2007,26(12):84-87.

[5] 张栋梁,杨林德,谢永利,等.盾构隧道抗震设计计算的解析解[J].岩石力学与工程学报,2008,27(3):543-549.

[6] 楼梦麟,潘旦光.滞后阻尼在土层时域分析中的应用[J].同济大学学报(自然科学版),2004,32(3):281-285.

[7]Clough R W,Penzien J.Dynamics of structures[M].New York:Mc Graw-Hill,1993.

[8] 张 昕.高架轨道交通引起环境振动的实测和理论分析研究[D].上海:同济大学土木工程学院,2002.

[9] 蒋 溥,戴丽思.工程地震学概论[M].北京:地震出版社,1993.

[10] Bathe K J,Wilson E L.Numerical methods in finite element analysis[M].Englewood Cliffs,New Jersey:Prentice-Hall,Inc,1976.

[11] 石礼安.地铁一号线工程[M].上海:上海科学技术出版社,1998.

[12] 沈 霞.地铁振动计算分析中的若干问题研究[D].上海:同济大学土木工程学院,2005.