负二项分布在区域自主创新评价中的应用

徐 晟, 徐 媛, 赵惠芳

(合肥工业大学管理学院,安徽合肥 230009)

0 引 言

自主创新能力的强弱体现了一个国家和地区的科技发展水平,也是决定一个国家和地区的综合竞争力的关键因素[1,2]。为更好地促进区域的技术进步和自主创新,研究区域自主创新的影响因素,并在区域自主创新评价指标体系的基础上找出合适的评价模型进行评价,对区域的自主创新发展和提高区域自主创新能力,具有深远的理论和实践意义。

国内外学者的研究表明,专利活动与创新关系密切,而且多年来专利标准客观、变化缓慢,是衡量创新活动相当可靠的指标,发明专利申请量是评价区域自主创新输出的主要度量之一[3],而专利到来可以被认为是一种遵循泊松分布的生产函数,泊松分布模型是最基本、最典型的发明专利的评价模型[4,5],也是区域自主创新评价模型之一。但在处理具体样本数据时,需要考虑样本之间的差异性来改进泊松模型。我国各省市的经济基础、区域文化及区域创新体系等各有差异,在运用泊松模型时应该考虑到这些差异性,需要对泊松模型进行进一步改进。

本文在建立区域自主创新评价指标体系的基础上,分析泊松分布评价模型的不足,构建了负二项分布的区域自主创新的评价模型,并将其应用于我国区域自主创新的评价上。通过实验和讨论,说明了该模型在对我国区域自主创新的评价是可行和有效的。

1 区域自主创新评价的指标体系设计

(1)区域自主创新评价指标体系。区域自主创新的影响因素很多,国内外学者主要从区域的创新基础设施水平、企业的创新投入、政府对创新的管理和组织及区域内产学研联系程度等几个方面进行研究[6-8]。

提供完善的创新基础设施有助于区域内企业提高技术能力,促进社会经济科技水平提高,对区域自主创新有极其重要的意义。区域的创新基础设施水平主要通过区域内的经济基础、教育条件和创新资源积累来体现;在区域自主创新中,企业是决策主体,也是投资主体,更是促进科技成果转化和应用的主体,在建设创新型企业和创新型区域的过程中,企业的创新投入具有重要作用。

企业的投入主要通过企业的人力资源和财力投入反映;高校和科研机构是新知识的缔造者,是创新的源头。在世界范围内,技术创新的主体是企业,但人类已经进入新经济时代,科学技术进步的程度与产业发展日新月异,高等院校和科研机构同企业的紧密联系是推动企业技术创新和整个区域自主创新的重要途径;政府在区域自主创新系统中发挥着其他主体难以发挥的作用,同时也是这个机制重要的参与者,可以通过政府的导向投入和吸引外商直接投资,来促进区域竞争和学习机制的形成。

为了使得评价指标体系各因素定量化,需要找出影响因素的替代变量,在借鉴国内外学者研究的基础上,本文提出了区域自主创新评价指标体系的主要影响因素,见表1所列。

表1 区域自主创新的主要影响因素

(2)区域自主创新的度量。专利是一个区域科技资产的核心和最富经济价值的部分,专利的拥有量既能反映该区域对科技成果的原始创新能力,又能折射出这些成果的市场应用潜能,它是衡量区域创新能力和综合实力的重要标志之一[9,10]。国内外经济学界常采用专利申请量而不是专利授权量来衡量创新,指出专利授权量受到政府专利机构等人为因素的影响较大,使得专利授权量由于不确定性因素增大而容易出现异常变动,并进一步指出专利申请量比专利授权量更能反映创新的真实水平[11]。

专利申请量是发明专利、实用新型专利和外观设计专利的总和,其中,发明专利技术的拥有量是衡量一个企业或一个区域创新能力的最好尺码。本文选用发明专利作为区域自主创新产出的度量指标,为理解中国区域自主创新能力演化的过程,提供了一个新的视角。

2 区域自主创新评价模型

区域自主创新评价问题是一个非常复杂的非线性问题,其输入输出关系很难用一个表达式直接给出,从数学建模的角度看,这种输入输出关系只能用一种映射关系抽象地表达。区域自主创新影响因素与输出(发明专利申请量)之间的关系可以表达为:

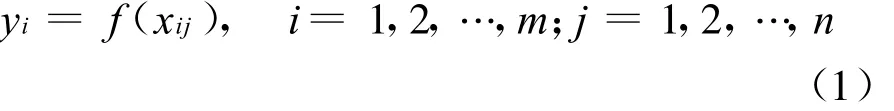
其中,yi为第i个区域发明专利申请总量;f为输入输出之间的映射关系;xij表示第i个区域的第j个指标变量。

这种映射关系没有明确的表达式,但是基于对区域自主创新的评估,需要在发明专利活动特性中找出规律,专利的决定性因素可以被认为是一种遵循泊松分布的生产函数,由于专利的产生是不确定的,描述独立随机事件产生的泊松模型适合用来估计专利生产函数。泊松分布模型是最基本、最典型的专利计算模型,这种概率计算是由泊松分布决定的。但是在具体评价区域自主创新活动时,应该考虑各个区域的差异及不可预知的因素的影响,这就需要在泊松评价模型基础上进行改进,引入新的评价模型。

(1)区域自主创新评价的泊松分布模型。在简单的泊松分布模型中,设pit是在t年i省发明专利总数,则根据pn=λit/n有如下关系式:

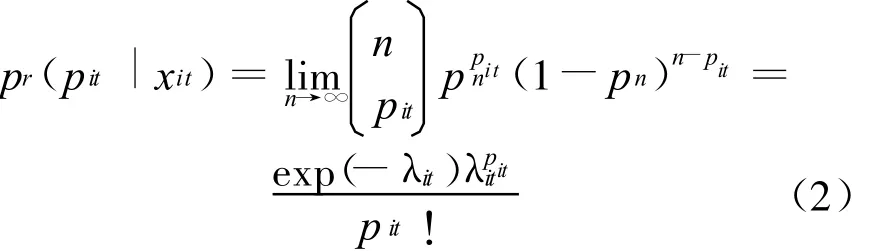
由于泊松分布的性质可得:

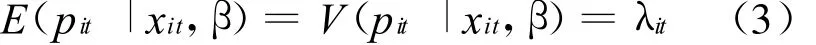
其中,β是被估计参数的矢量,通过极大似然估计可以得出:

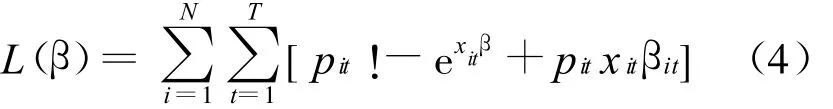
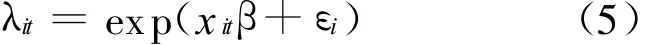
(2)区域自主创新评价的负二项分布模型。发明专利计算的负二项模型比泊松模型更为普遍,因为它允许均值方程的差异,这样就放宽了变量的限制。负二项分布与泊松分布相同,但条件变量不同:

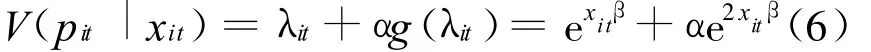
其中,α是未知的分散参数,而且当α增加时,发明专利数量pit增加。当条件变量是均值的二次方时,结果为负二项分布模型[12-14],即:

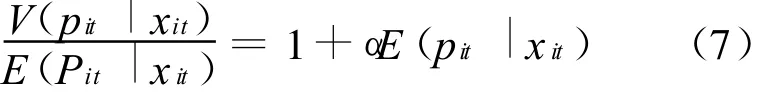
负二项模型是作为泊松和伽玛分布的混合模型获得的。伽马分布密度函数如下:

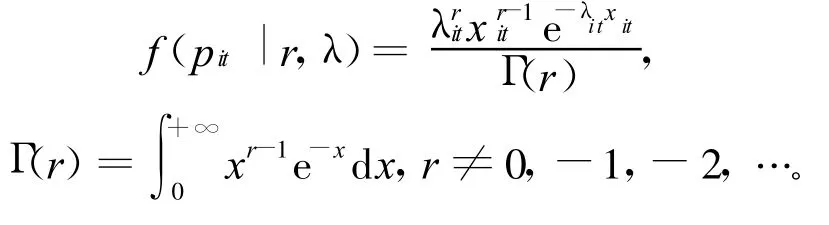
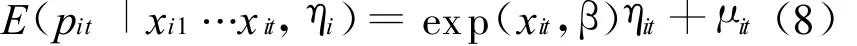
3 负二项分布评价实验

(1)实验结果。为了比较泊松模型和负二项分布模型对自主创新的评价效果,本文首先选取了自主创新评价的全国2000-2006年数据,分别在SAS8.0软件平台上运行,2个模型运行的拟合结果见表2、表3所列。

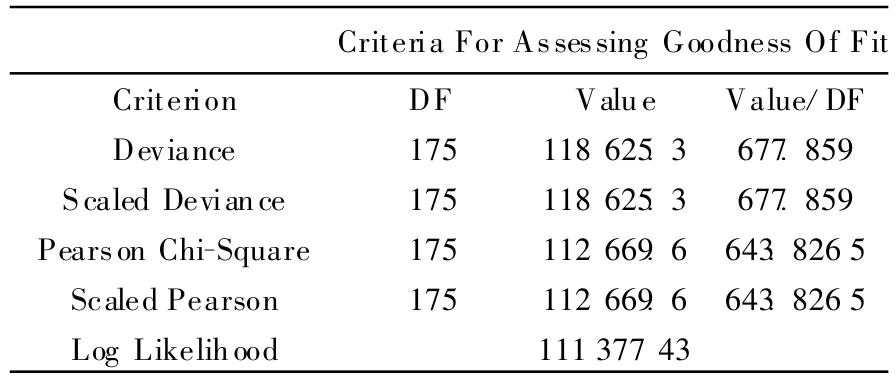
表2 基于泊松分布模型的拟合结果

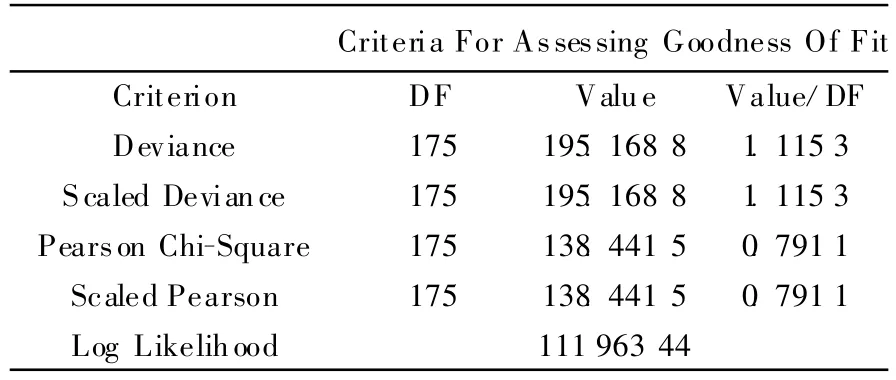
表3 基于负二项分布模型的拟合结果

表2、表3中,DF表示样本自由度,即有效样本个数;Deviance与Pearson Chi-Square表示偏差与皮尔森卡方,是SAS GENMOD模型评价拟合优度的2个统计量,由软件计算所得,其与DF的比值越接近于1,说明拟合优度越好;Scaled表示尺度参数,SAS软件允许规定一个尺度参数来拟合过于分散的泊松分布和负二项分布,由软件自动计算所得。一般与尺度调整前偏差不大。

根据表2的结果,由于Deviance和Pearson Chi-Square远大于1,说明数据拟合过渡离散,结果很不理想。从表3可以看出,Deviance和Pearson Chi-Square与DF的比值均接近于1,拟合效果较优。从而证明在拟合专利生产的模型过程来进行自主创新的评价中,使用负二项分布的效果明显优于泊松分布。

由于我国各个区域适用的相同的专利法及其环境,专利生产过程具有类似性,从上面的结果可以看出,在运用专利生产过程评价自主创新中负二项分布模型优于泊松分布模型。因此对区域的评价过程中,运用负二项分布模型进行评价,并对结果进行讨论,进一步证实负二项分布模型进行评价自主创新的合理性。

文章选取的样本为大陆的东中西部地区共31个省和直辖市,数据的跨度同样为2000-2006年。数据来源于《中国科技统计年鉴》、《中国统计年鉴》、《中国城市统计年鉴》以及中华人民共和国国家知识产权局网站。由于发明专利的出现具有滞后性[15],本文选择了各省市输入指标滞后一年的面板数据,输出的发明专利数为当年的数值。

通过负二项分布模型在SAS8.0软件平台上的运行,结果见表4所列。表4中Value/DF表示模型拟合程度,从表4中的离散系数和拟合度来看,负二项分布运用于区域自主创新的评价是可行的。

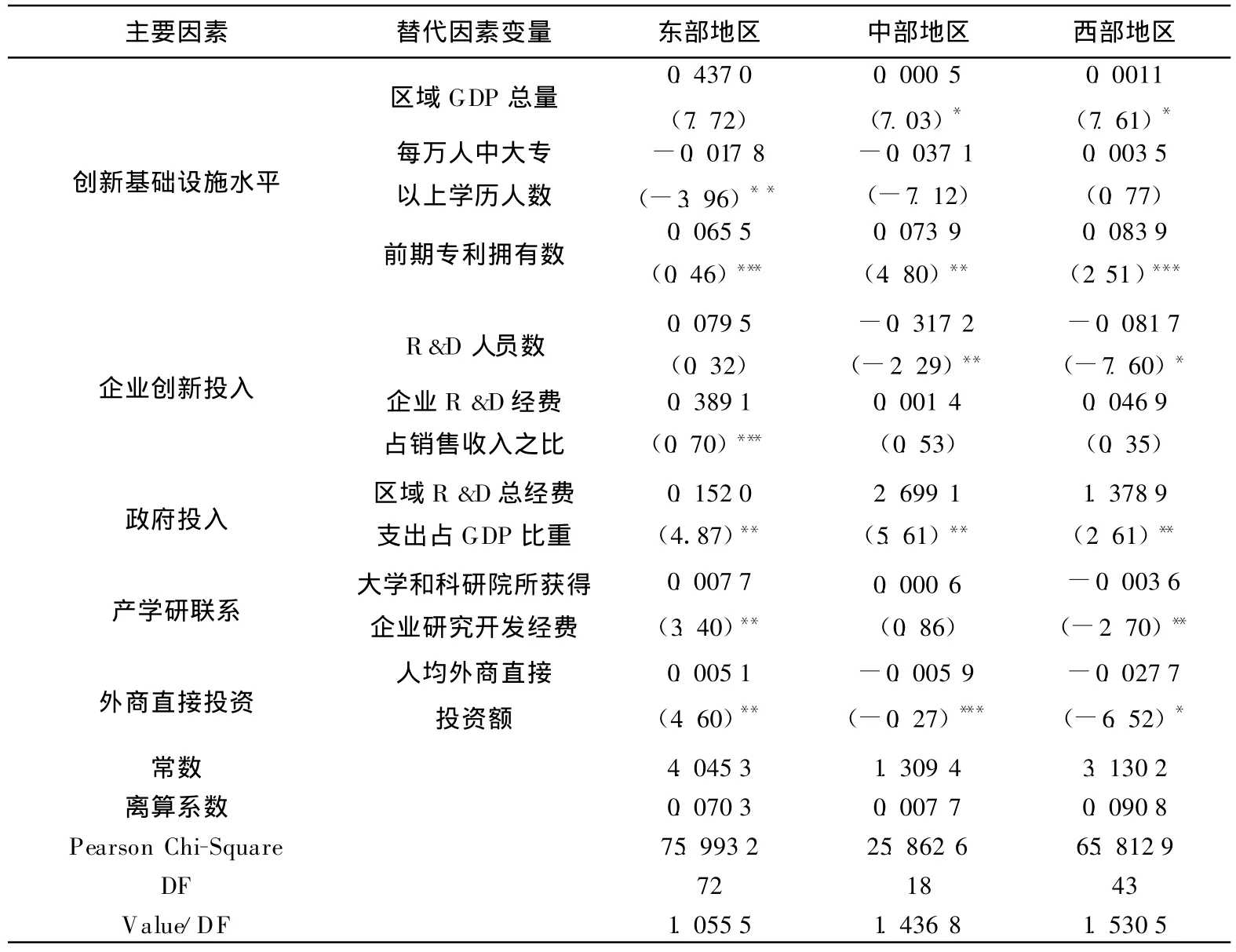
表4 区域自主创新评价结果

(2)讨论。通过对表4评价结果的分析,总体可以看出,东部地区的自主创新情况明显优于中西部地区,中西部地区的情况较为类似。我国虽然实施了一些促进中西部地区发展的战略,这些战略也在一定程度上对中西部地区经济的发展,自主创新能力的提升起到了积极的促进作用,但东部地区以更快的速度在发展。

因此,我国区域之间的差距仍很显著,中西部地区在提高自主创新能力,谋求自身发展方面还有很长的路要探索。

此外,上述分析结果也验证了“中部地区塌陷”的问题,中部地区的创新能力不仅和东部地区存在较大的差异,甚至在很多方面低于西部,这些结论与国内大部分学者的研究结论相一致。从输出的研究结果看,负二项分布运用于区域自主创新的评价是有效的。

4 结束语

本文在区域自主创新评价指标体系研究的基础上,进一步分析泊松模型的不足,提出了负二项分布的区域自主创新评价模型。

从实验输出的结果来看,负二项分布运用于区域自主创新的评价是可行的,从研究讨论的结论来看,负二项分布运用于区域自主创新的评价是有效的,为国家和区域的自主创新能力评价提供了一个良好的研究工具。进一步的研究除了要考虑影响因素之外,还需要考虑其他定性与定量相结合的评价模型。

[1] Amir R,Jin J Y,T roege M.On additive spillovers and returns to scale in R&D[J].International Journal of Industrial Organization,2008,26(3):695-703.

[2] Amara N,Landry R,Traoré N.Managing the protection of innovations in knowledge-intensive business services[J].Research Policy,2008,37(9):1530-1547.

[3] Ramani S V,El-A roui M A,Carrè re M C.On estimating a knowledge production function at the firm and sector level using patent statistics[J].Research Policy,2008,37(8):1568-1578.

[4] Deiss R.Intellectual property organizations and pharmaceutical patents in Africa[J].Social Science&Medicine,2007,64(2):287-291.

[5] Bae S,Famoye F,Wulu J T,et al.A rich family of generalized Poisson regression models with applications[J].Mathematics and Computers in Simulation,2005,69(1):4-11.

[6] Deng Yi.T he value of knowledge spillovers in the U.S.semiconductor industry[J].International Journal of Industrial Organization,2008,26(4):1044-1058.

[7] 徐 晟,赵惠芳,孙朝华.基于灰色模型的企业技术创新影响因素分析[J].合肥工业大学学报(自然科学版),2005,28(8):845-849.

[8] Wagner M.On the relationship between environmental management,environmental innovation and patenting:evidence from German manufacturing firms[J].Research Policy,2007,36(10):1587-1602.

[9] Anthony A.T he relative effectiveness of patents and secrecy for appropriation[J].Research Policy,2001,30:611-624.

[10] 潘雄锋,刘凤朝.中国专利申请结构的分析与预测[J].情报杂志,2005,(2):76-78.

[11] Encaoua D.Patent systems for encouraging innovation:lessons from economic analysis[J].Research Policy,2006,35:1423—1440.

[12] 汪学海,祝家麟,林 鑫,等.泊松方程的边界节点解法[J].重庆大学学报(自然科学版),2007,30(12):84-88.

[13] 刘瑞元,张智霞.二项分布与泊松分布判别的假设检验[J].青海大学学报(自然科学版),2008,26(1):44-47.

[14] 唐军民,王成名.负二项分布可靠度的经验Bayes估计[J].工程数学学报,2005,22(6):1039-1047.

[15] Wu Y C J,Lee P J.The use of patent analy sis in assessing ITS innovations:US,Europe and Japan[J].Transportation Research Part A:Policy and Practice,2007,41(6):568-586.